 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Для расчета калькулятора
Задание: Используя экспериментальные данные по адсорбции бензола на графитированной термической саже при нескольких температурах:
1. Постройте три изотермы адсорбции. 2. Рассчитайте константы уравнения Лэнгмюра и удельную поверхность адсорбента ( 3. Рассчитайте интегральную теплоту адсорбции. 4. Для А=0,005 моль/кг; А=0,01 моль/кг; А=0,015 моль/кг постройте изостеры адсорбции по которым рассчитайте дифференциальную теплоту адсорбции. Проанализируйте полученные результаты.
Решение: 1. По экспериментальным данным строим три изотермы адсорбции бензола на графитированной саже:
Рис.5. Изотермы адсорбции: 1 – Т=293К; 2 – Т=303 К; 3 – Т=313 К.
2.Для построения изотермы Лэнгмюра в линейных координатах рассчитаем значения р/А для каждого значения р для трех температур. Рассчитанные данные занесем в таблицу:
По рассчитанным данным построим изотермы Лэнгмюра в линейных координатах при трех температурах:
Рис. 6. Изотермы адсорбции в линейных координатах: 1 – Т=293 К; 2 – Т=303 К; 3 – Т=313 К.
3. Графически рассчитываем константы уравнения Лэнгмюра, полученные данные заносим в таблицу: Т1 = 313 К
Т2 = 303 К
Т3 = 293 К
Результаты расчета занесем в таблицу:
Из таблицы следует, что величина предельной адсорбции (
4. Рассчитаем удельную поверхность адсорбента по уравнению (6):
5. Для расчета интегральной теплоты адсорбции построим график зависимости
Рис.7. Линейная зависимость ln К от обратной температуры. Рассчитаем тангенс угла наклона прямой и интегральную теплоту адсорбции по уравнению (9):
Таким образом, процесс адсорбции бензола на графитированной термической саже идет с выделением тепла (экзотермический процесс).
6. Для построения трех изостер адсорбции при А=0,005 моль/кг; А=0,010 моль/кг; А=0,015 моль/кг проведем к изотермам адсорбции (рис.5) три линии, параллельные оси абсцисс. Составим таблицу зависимости давления от температуры при постоянной величине адсорбции:
Рис. 8. Изотермы адсорбции: 1 – Т=293К; 2 – Т=303 К; 3 – Т=313 К.
Построим три изостеры адсорбции для А=0,005 моль/кг; А=0,010 моль/кг и А=0,015 моль/кг.
Рис. 9. Изостеры адсорбции: 1 – А=0,015 моль/кг; 2 – А=0,010 моль/кг и 3 – А=0,005 моль/кг.
7. Для расчета изостерической дифференциальной теплоты адсорбции построим график в координатах
Рис.10. Линейная зависимость ln р от обратной температуры: 1 - А=0,015 моль/кг; 2 - А=0,010 моль/кг; 3 - А=0,005 моль/кг.
Рассчитаем тангенсы углов наклона полученных прямых и дифференциальные теплоты адсорбции для А=0,005 моль/кг; А=0,010 моль/кг и А=0,015 моль/кг по уравнению (11): 1. 2. 3. Из полученных результатов следует, что изостерическая теплота адсорбции слабо зависит от степени заполнения поверхности. Это свидетельствует о том, что поверхность адсорбента (графитированной сажи) достаточно однородна. Рассчитанные значения qA свидетельствуют о том, что адсорбция бензола на графитированной термической саже обусловлена, в основном, физическими силами.
Поиск по сайту: |
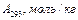


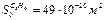 ).
).
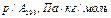
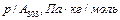



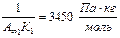 ,
, 

 ,
, 

 ,
, 

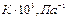
 ) постоянна при разных температурах и зависит только от природы адсорбента и адсорбата. Константа адсорбционного равновесия К уменьшается с увеличением температуры.
) постоянна при разных температурах и зависит только от природы адсорбента и адсорбата. Константа адсорбционного равновесия К уменьшается с увеличением температуры.
 , предварительно составив таблицу:
, предварительно составив таблицу:



 .
.

 для различных значений адсорбции. Предварительно составив таблицу:
для различных значений адсорбции. Предварительно составив таблицу:


