 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теория мономолекулярной адсорбции Лэнгмюра
1. Адсорбция молекул адсорбата происходит на активных центрах, всегда существующих на поверхности адсорбента. Активные центры адсорбента энергетически равноценны. 2. Каждый активный центр может адсорбировать только одну молекулу адсорбата. В результате этого на поверхности адсорбента образуется мономолекулярный слой адсорбата. 3. Адсорбированные молекулы не взаимодействуют друг с другом. Поэтому время пребывания молекул на активных центрах не зависит от того, заняты молекулами соседние активные центры или нет. 4. Адсорбция носит динамический характер. Адсорбат удерживается на поверхности адсорбента некоторое время, а потом десорбируется.
На основе приведенных исходных положений Лэнгмюром было предложено уравнение изотермы мономолекулярной адсорбции, которое для адсорбции газов на однородной твердой поверхности имеет вид:
где р – равновесное давление адсорбтива; К – константа адсорбционного равновесия, характеризующая энергию взаимодействия адсорбата и адсорбента; А∞ – предельная адсорбция (емкость адсорбционного монослоя). Типичный вид изотермы Лэнгмюра показан на рис. 1. На изотерме адсорбции Лэнгмюра выделяют три участка:
Расчет констант уравнения Лэнгмюра Константы (К и А∞) уравнения Лэнгмюра рассчитывают графическим способом, для этого уравнение (1) приводят к линейному виду: y=a+bx.
Строят изотерму адсорбции в координатах линейной формы уравнения Лэнгмюра (рис.2):
Зная величину
где S0 – площадь, занимаемая одной молекулой адсорбата, NA – число Авогадро. Представления, развитые Лэнгмюром, в значительной степени идеализируют и упрощают действительную картину адсорбции. На самом деле поверхность большинства адсорбентов энергетически неоднородна, между молекулами адсорбата имеют место «боковые» взаимодействия.
Установив экспериментальную зависимость константы адсорбционного равновесия К от температуры, можно определить энтальпию адсорбции (интегральную теплоту адсорбции). Интегральная теплота адсорбции характеризует интенсивность взаимодействия адсорбента с адсорбатом (газом или паром), она отрицательна, что указывает на выделение теплоты в процессе адсорбции и не зависит от степени заполнения адсорбента газом. Уравнение (7) применяют для определения интегральной теплоты адсорбции графическим способом, для этого уравнение (7) интегрируют (неопределенный интеграл):
где В ─ постоянная интегрирования.
Аналитический способ расчета интегральной теплоты адсорбции основан на уравнении:
Каждой степени заполнения поверхности адсорбента соответствует некоторая дифференциальная теплота адсорбции qA. Дифференциальная изостерическая (A = const) теплота адсорбции всегда положительна и уменьшается по мере роста степени заполнения адсорбатом поверхности адсорбента. Если значения qA невелики (10 – 40 кДж/моль), то можно говорить о физической адсорбции газов, обусловленной физическими силами. Если рассчитанные значения qA находятся в пределах 40 – 400 кДж/моль, то в этом случае адсорбция обусловлена химическими силами (хемосорбция). Для расчета qA строят изостеры адсорбции (зависимости р от Т) при разных температурах (A = const). Для построения изостер адсорбции проводят к изотермам адсорбции линии, параллельные оси абсцисс. Графически находят значения р и Т при разных А.
Аналитический способ расчета дифференциальной теплоты адсорбции основан на уравнении:
Поиск по сайту: |
 , (1)
, (1) Рис.1. Изотерма мономолекулярной адсорбции Лэнгмюра в координатах А=f(p).
Рис.1. Изотерма мономолекулярной адсорбции Лэнгмюра в координатах А=f(p).
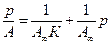 . (2)
. (2) Рис.2. Изотерма адсорбции в координатах линейной формы уравнения Лэнгмюра.
Рис.2. Изотерма адсорбции в координатах линейной формы уравнения Лэнгмюра.
 . (3)
Тангенс угла наклона прямой равен:
. (3)
Тангенс угла наклона прямой равен:
 , (4)
или
, (4)
или  . (5)
. (5)
 , можно рассчитать удельную поверхность адсорбента:
, можно рассчитать удельную поверхность адсорбента: , (6)
, (6) Рис. 3. Изотермы адсорбции пи различных температурах (Т1 > T2 > T3)
Рис. 3. Изотермы адсорбции пи различных температурах (Т1 > T2 > T3)
 (7)
(7)
 , (8)
, (8) Рис.4. Линейная зависимость ln К от обратной температуры.
Рис.4. Линейная зависимость ln К от обратной температуры.
 (9)
(9)
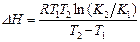 . (10)
. (10) Рис.5. Линейная зависимость ln р от
обратной температуры.
Рис.5. Линейная зависимость ln р от
обратной температуры.
 (рис.5) по уравнению:
(рис.5) по уравнению:
 (11)
(11)
 . (12)
. (12)