 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Відповідно до рівняння Дюпюі
Відокремимо перемінні і проінтегруємо від перетину 1 до перетину М:
а на всієї віддалі від перетину 1 до перетину 2 :
тоді Для кінцевого перетину (на урізі правої річки), де x = L1-2
Визначення відстані до вододілу. Наявність інфільтрації приводить до виникнення на поверхні ґрунтових вод підземного вододілу. При цьому рух підземних вод від вододілу в сторону річоки відрізняється. Витрата через перетин на вододілі дорівнює нулю (qx = 0). Позначивши відстань до вододілу через а, і враховуючи що qx = 0, знайдемо а:
Якщо h1 = h2, то а= якщо h1 > h2, то а< якщо h1 < h2 , то а> Значення а може бути негативним (а<0) або більше L1-2, коли вододіл знаходиться за межами межирічного масиву. Побудова кривої депресії . Використовуючи рівняння
визначимо ординату кривої депресії на відстані x від лівої річки. Для знаходження q1 необхідно розв’язати інше рівняння відносно hx,
звідси з врахуванням q1 звідки: Це рівняння эліпса. Отже, у межирічному масиві крива депресії ґрунтових вод при наявності інфільтраційного живлення описується рівнянням еліпса , при відсутності інфільтраційного живлення - рівнянням параболи Максимальна потужність ординати кривої депресії знаходиться на вододілі і тому прийнявши х = а в попередньому рівнянні можна одержати hmax
Розрахунок витрат і ординат депресії межирічних потоків ґрунтових вод з похилим заляганням водоупора складний і ще недостатньо розроблений, тому на практиці звичайно водотривку основу умовно вважають горизонтальнею. Потоки підземних вод у межирічному масиві неоднорідного будівлі. Припустимо що W=const і горизонтальне залягання водоупора i =0. Нехай у межах межиріччя є 2-і ділянки: L1, де k1 і L2 , де k2 Складемо рівняння для одиничної витрати на межі 2-х фрагментів використовуючи формулу:
для фрагмента 1-S
для фрагмента S-2
В силу нерозривності потоку приплив підземних вод до правої межі лівого фрагмента дорівнює їх відтоку від лівої межі правого фрагмента, тому праві частини цих формул можна порівняти:
звідки
Завдання Задача 1.(Для варіанта 1). Межиріччя шириною 9км складено тріщинуватими вапняками, які підстилаються щільними глинами що залягають горизонтально . Потужність водонасичених вапняків в рік 83м і 75м. Коефіцієнт фільтрації 26м/доб. В інфільтраційному живленні беруть участь лише 30% річної кількості опадів, що досягає 380мм. Необхідно визначити одиничну витрату підземних вод у річці і побудувати депресійну криву.
Таблиця 1.Вихідні дані по варіантах для задачі 1.
Задача 2. (Для варіанта 1). Відстань від річки до каналу дорівнює 1730м. На цій відстані водоносні алювіальні піски з коефіцієнтом фільтрації 10.0м/сут. Середня річна кількість опадів характеризується величиною 520мм. В інфільтраційному живленні бере участь тільки 31% цих опадів. Рівні води в ріці і каналі знаходяться на відмітках відповідно 34.0м і 33.0м. Водотривке ложе щільних глин залягає похило з відмітками 20.0м у річки і 24.0м у каналі. Визначити величини одиничної витрати підземного стоку в річку і канал, відстань до вододілу, ординату вододілу, а також побудувати депресійну криву. Таблиця 2. Вихідні дані по варіантах для задачі 2.
Тема 4
Поиск по сайту: |
 , тоді
, тоді  (2)
(2) , одержимо для одиничної витрати:
, одержимо для одиничної витрати: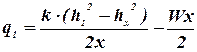 (3)
(3) , (4)
, (4) (5)
(5) (6)
(6) (7)
(7) , тобто вододіл посередині,
, тобто вододіл посередині, (9)
(9) (10)
(10)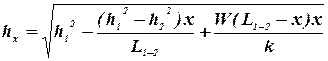 (11)
(11) (12)
(12) (14)
(14) (15)
(15)
 (16)
(16) (17)
(17)