 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Порядок виконання роботи. 1. Зібрати схему згідно рис
1. Зібрати схему згідно рис. 2. 2. Ввімкнути осцилограф. З. Добитися чіткого зображення розгорненого променя на екрані. 4. Ввімкнути генератор П- подібних імпульсів. Подати напругу на осцилограф і добитися стійкого зображення коливань на екрані осцилографа. 5. Заміряти (в відносних одиницях) два сусідніх значення амплітуди для трьох значень активного опору 6. Розрахувати логарифмічний декремент і добротність коливальної системи для цих значень R. 7. Дані вимірювань і розрахунків занести в таблицю:
7. У висновках дати оцінку отриманому результату.
Завдання 2.
1. Мета роботи. Вивчити вимушені коливання в коливальному контурі. Визначити залежність амплітуди струму в коливальному контурі від частоти і залежність резонансної частоти від активного опору R, індуктивності L і ємності С.
Теоретичні відомості. В техніці дуже часто потрібні незгасаючі коливання. Наприклад, в коливальних контурах радіопередавачів. Незгасаючі – це вимушені коливання, коливання, що виникають під дією додаткової змінної зовнішньої сили, яка поповнює зменшення енергії в коливальному контурі. Нехай в коливальному контурі діє змінна ЕРС
Рис. 4
За другим законом Кірхгофа:
Звідси маємо:
або
де
Розв’язком диференціального рівняння (15) є гармонічна функція:
Амплітуда
Напруга на конденсаторі змінюється так само, як і заряд:
Амплітуда напруги (і заряду) залежить від частоти. Знайдемо вираз для сили струму. Використовуючи (18), маємо:
де
Підставимо в (23) вираз для
Враховуючи, що
Тут При
Рис. 5.
При резонансі амплітуда струму
На графіку залежність амплітуди струму від частоти зображується наступним чином:
Рис. 6.
При
Опис установки. Дослідити залежність амплітуди струму від частоти, а також залежність резонансної частоти від індуктивності та ємності можна за допомогою наступної установки.
Рис. 7.
В коливальному контурі, який складається із активного опору R, індуктивності L і ємності С діє вимушуюча ЕРС. Міняючи її частоту, можна добитися резонансу струму в коливальному контурі (при Про величину струму судимо по напрузі на деякому невеликому опорі
Поиск по сайту: |
 .
.
 .
.


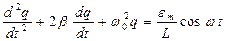 , (15)
, (15) (16)
(16) . (17)
. (17) . (18)
. (18) і початкова фаза Ψ визначаються із співвідношень:
і початкова фаза Ψ визначаються із співвідношень: (19)
(19) (20)
(20) (21)
(21) . (22)
. (22) ,
,
 . (23)
. (23) . (24)
. (24) . (25)
. (25) - повний електричний опір, який складається із активного опору R, індуктивного
- повний електричний опір, який складається із активного опору R, індуктивного  та ємнісного
та ємнісного  .
. матимемо максимум амплітуди струму – резонанс струму. Звідси
матимемо максимум амплітуди струму – резонанс струму. Звідси  , тобто резонанс струму реалізується при резонансній частоті, яка дорівнює частоті власних коливань контуру. Збільшення ємності С чи індуктивності L зменшує резонансну частоту, що якісно зображено на рис. 5, а та б.
, тобто резонанс струму реалізується при резонансній частоті, яка дорівнює частоті власних коливань контуру. Збільшення ємності С чи індуктивності L зменшує резонансну частоту, що якісно зображено на рис. 5, а та б.
 стає максимальною і залежить від активного опору:
стає максимальною і залежить від активного опору:

 струм в коливальному контурі відсутній (через конденсатор постійний струм не протікає).
струм в коливальному контурі відсутній (через конденсатор постійний струм не протікає).
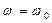 ).
). , яка подається на осцилограф.
, яка подається на осцилограф.