 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Прилади та обладнанняСтр 1 из 3Следующая ⇒
Вивчення затухаючих і вимушених коливань В коливальному контурі
Київ 2010
Лабораторна робота №10
Вивчення затухаючих і вимушених коливань В коливальному контурі Завдання 1. 1. Мета роботи. 1. Вивчити затухаючі коливання в коливальному контурі, визначити логарифмічний декремент і добротність досліджуваного контура.
Теоретичні відомості.
Наростання струму до деякого максимального значення відбувається за
Коливання, які з’явилися в контурі – гармонічні, проте в зв’язку з тим, що існує активний опір R, в якому виділяється тепло, амплітуда коливань зменшуватиметься. Тобто електромагнітні коливання в реальному коливальному контурі завжди є затухаючими. Встановимо закон і визначимо основні характеристики затухаючого коливального процесу. Згідно другого закону Кірхгофа алгебраїчна сума спадів напруг дорівнює алгебраїчній сумі ЕРС, працюючих в контурі:
де Запишемо (1) у вигляді:
або, враховуючи, що
Позначимо
Тоді вираз (2) можна записати:
Розв’язком цього рівняння буде гармонічна функція:
де За аналогічним законом відбуваються і коливання напруги на конденсаторі:
Величина
є амплітудою даного гармонійного коливання, проте ця амплітуда експоненціально зменшується з часом. Такі коливання називаються затухаючими. Вони відбуваються з частотою
де відповідно до (3), (4)
де
де З (8) випливає, що при затухаючих коливаннях частота ω менша за частоту ω0 власних коливань. На графіку незатухаючі і затухаючі коливання можна показати наступним чином (див. рис. 2). Пунктирною лінією показано зменшення амплітуди з часом. Згідно (7) і (10), чим більше β (тобто ніж більше R), тим швидше відбувається затухання. Порівняємо значення амплітуди двох сусідніх моментів часу, розділених періодом Т:
Співвідношення
називається декрементом затухання.
Рис. 2.
В радіотехніці коливальні контури прийнято характеризувати добротністю. Добротність визначається відношенням повної енергії коливань в контурі до втрат енергії за період:
Повна енергія коливального контуру може бути виражена через амплітуду
Оскільки
Припустимо, що енергія не дуже сильно змінюється за період. Тоді можна прийняти
Звідси маємо
Підставимо це значення в (13). Тоді отримаємо
Таким чином, знаючи коефіцієнт загасання β або логарифмічний декремент δ, можна визначити добротність коливальної системи (коливального контуру). Добротність коливальних контурів досягає значень ~102 і вище.
Опис установки. Для вивчення затухаючих коливань потрібно зібрати схему з генератором затухаючих коливань, яке зручно розглядати на екрані осцилографа. Така схема представлена на рис. 3.
Рис. 3.
На коливальний контур, що складається з конденсатора С, індуктивності L, і опору R, від генератора через подільчий конденсатор Вмикаючи в коливальний контур різні активні опори, можна вивчити їх вплив на характер затухання коливань.
Прилади та обладнання. 1. Установка для вивчення затухаючих коливань. 2. Генератор П-подібних імпульсів. 3. Осцилограф. 4. З’єднувальні провідники.
Поиск по сайту: |
 Електромагнітні коливання відіграють дуже важливу роль в техніці і, зокрема, в техніці зв'язку. Електромагнітні коливання виникають в коливальному контурі, що складається з конденсатора С, котушки індуктивності і активного опору R. Якщо зарядити конденсатор С, замкнути ключ К, то конденсатор стане розряджатися. В колі потече струм, який повільно наростатиме через виникаючий струм самоіндукції. При цьому енергія електричного поля конденсатора С буде переходити в енергію магнітного поля котушки.
Електромагнітні коливання відіграють дуже важливу роль в техніці і, зокрема, в техніці зв'язку. Електромагнітні коливання виникають в коливальному контурі, що складається з конденсатора С, котушки індуктивності і активного опору R. Якщо зарядити конденсатор С, замкнути ключ К, то конденсатор стане розряджатися. В колі потече струм, який повільно наростатиме через виникаючий струм самоіндукції. При цьому енергія електричного поля конденсатора С буде переходити в енергію магнітного поля котушки. періоду. Протягом наступного
періоду. Протягом наступного 
 , (1)
, (1) - напруга на конденсаторі;
- напруга на конденсаторі;  - ЕРС самоіндукції.
- ЕРС самоіндукції.
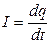 :
: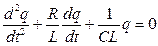 (2)
(2) (3)
(3) (4)
(4)
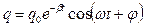 , (5)
, (5) – максимальний заряд на обкладинках конденсатора в початковий момент.
– максимальний заряд на обкладинках конденсатора в початковий момент. . (6)
. (6) (7)
(7) , (8)
, (8) , (9)
, (9) - частота власних коливань, тобто в ідеалізованому контурі, коли його активний опір R=0, а
- частота власних коливань, тобто в ідеалізованому контурі, коли його активний опір R=0, а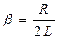 , (10)
, (10) - коефіцієнт затухання.
- коефіцієнт затухання.
 (11)
(11)
 . (13)
. (13)
 , де
, де  - повна енергія коливань в початковий момент. Знайдемо швидкість зміни енергії:
- повна енергія коливань в початковий момент. Знайдемо швидкість зміни енергії: .
. і для швидкості зміни енергії можемо записати (по абсолютній величині):
і для швидкості зміни енергії можемо записати (по абсолютній величині): .
.
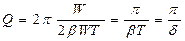 . (14)
. (14)
 подаються періодичні П- подібні імпульси напруг. Кожен імпульс збуджує в коливальному контурі затухаючі коливання. Ці коливання накладаються одне на одне і на екрані осцилографа можна отримати стійку картинку затухаючих коливань.
подаються періодичні П- подібні імпульси напруг. Кожен імпульс збуджує в коливальному контурі затухаючі коливання. Ці коливання накладаються одне на одне і на екрані осцилографа можна отримати стійку картинку затухаючих коливань.