 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Приближенная теория гироскопа ⇐ ПредыдущаяСтр 2 из 2
Гироскопом называют тело, имеющее неподвижную точку и вращающееся вокруг оси материальной симметрии. Предположим, что гироскоп вращается с угловой скоростью вокруг собственной оси симметрии. В этом случае кинетический момент
Это одна из важнейших характеристик при движении гироскопа.
В приближенной теории гироскопа принимают, что 1 << и кинетический момент гироскопа равен
Гироскоп с тремя степенями свободы Гироскоп с тремя степенями свободы способен сопротивляться попытке изменения оси вращения гироскопа. Рассмотрим гироскоп, у которого неподвижная точка совпадает с центром масс. Рассмотрим сначала покоящийся гироскоп ( = 0, L = 0). Если к гироскопу приложить силу Рассмотрим вращающийся (быстро) гироскоп. Прикладываем силу По теореме об изменении кинетического момента
Момент перпендикулярен к плоскости чертежа, тогда
Если к оси гироскопа прикладывается сила, то ось гироскопа смещается перпендикулярно действующей силе по направлению вращающего момента. Если действие силы прекращается, то ось вращения гироскопа останавливается. ^ Говорят, что гироскоп способен противодействовать действию внешних сил. Рассмотрим случай регулярной прецессии. Имеется гироскоп, у которого центр масс не совпадает с неподвижной точкой. На тело действует сила Допустим OC = h, тогда
Отметим: Под действием силы тяжести ось гироскопа будет вращаться вокруг вертикальной оси z. Такое явление называется регулярной прецессией. Введем угловую скорость 1 – это угловая скорость, с которой ось гироскопа вращается вокруг оси z, ее еще называют “угловая скорость прецессии”.
Движение юлы – очень хороший пример движения гироскопа. Гироскоп с тремя степенями свободы находит широкое применение в современных системах ориентирования (гирокомпас, гирогоризонт …). Билет 12 Вопрос 1 Если голономная механическая система описывается лагранжианом
где i = 1, 2, … n (n — число степеней свободы механической системы). Лагранжиан представляет собой разность кинетической и потенциальной энергий системы. Количеством движения системы материальных точек называется векторная сумма количеств движений отдельных точек системы. Единицей измерения количества движения в СИ является — Количество движения системы можно выразить через массу системы и скорость центра масс. Количеством движения (импульсом) механической системы называют величину, равную сумме количеств движения (импульсов) всех тел, входящих в систему. Импульс внешних сил, действующих на тела системы, — это сумма импульсов всех внешних сил, действующих на тела системы. Теорема об изменении количества движения системы утверждает[2][3]: Изменение количества движения системы за некоторый промежуток времени равно импульсу внешних сил, действующих на систему, за тот же промежуток времени. Пусть система состоит из
Используя введённые обозначения, запишем второй закон Ньютона для каждой из рассматриваемых материальных точек в виде
Учитывая, что
Выражение
Используя для количества движения системы
Таким образом, каждое из последних полученных уравнений позволяет утверждать: изменение количества движения системы происходит только в результате действия внешних сил, а внутренние силы никакого влияния на эту величину оказать не могут. Проинтегрировав обе части полученного равенства по произвольно взятому промежутку времени между некоторыми
где
Поиск по сайту: |



 , то очевидно, что гироскоп получит вращательное движение и упадет (т.е. ось гироскопа будет поворачиваться в плоскости чертежа).
, то очевидно, что гироскоп получит вращательное движение и упадет (т.е. ось гироскопа будет поворачиваться в плоскости чертежа).




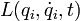 (
(  — обобщённые координаты, t — время, точкой обозначено дифференцирование по времени) и в системе действуют только потенциальные силы, то уравнения Лагранжа второго рода имеют вид
— обобщённые координаты, t — время, точкой обозначено дифференцирование по времени) и в системе действуют только потенциальные силы, то уравнения Лагранжа второго рода имеют вид
 материальных точек с массами
материальных точек с массами  и ускорениями
и ускорениями  . Все силы, действующие на тела системы, разделим на два вида:
. Все силы, действующие на тела системы, разделим на два вида: .
. , а силу воздействия i-й точки на k-ю точку —
, а силу воздействия i-й точки на k-ю точку —  . Очевидно, что при
. Очевидно, что при 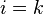 , то
, то 
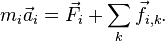
 и суммируя все уравнения второго закона Ньютона, получаем:
и суммируя все уравнения второго закона Ньютона, получаем:
 представляет собой сумму всех внутренних сил, действующих в системе. По третьему закону Ньютона в этой сумме каждой силе
представляет собой сумму всех внутренних сил, действующих в системе. По третьему закону Ньютона в этой сумме каждой силе  и, значит, выполняется
и, значит, выполняется  Поскольку вся сумма состоит из таких пар, то и сама сумма равна нулю. Таким образом, можно записать
Поскольку вся сумма состоит из таких пар, то и сама сумма равна нулю. Таким образом, можно записать
 обозначение
обозначение  , получим
, получим Введя в рассмотрение изменение импульса внешних сил
Введя в рассмотрение изменение импульса внешних сил  , получим выражение теоремы об изменении количества движения системы в дифференциальной форме:
, получим выражение теоремы об изменении количества движения системы в дифференциальной форме:
 и
и  , получим выражение теоремы об изменении количества движения системы в интегральной форме:
, получим выражение теоремы об изменении количества движения системы в интегральной форме: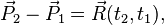
 и
и 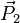 — значения количества движения системы в моменты времени
— значения количества движения системы в моменты времени  — импульс внешних сил за промежуток времени
— импульс внешних сил за промежуток времени  . В соответствии со сказанным ранее и введёнными обозначениями выполняется
. В соответствии со сказанным ранее и введёнными обозначениями выполняется