 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Принцип Даламбера для материальной точкиСтр 1 из 2Следующая ⇒
Билет 5 Вопрос 1
Вопрос 2 Условия равновесия механических систем. Согласно принципу возможных перемещений (основному уравнению статики), для того, чтобы механическая система, на которую наложены идеальные, стационарные, удерживающие и голономные связи, находилась в равновесии, необходимо и достаточно, чтобы в этой системе были равны нулю все обобщенные силы:
где Qj - обобщенная сила, соответствующая j -ой обобщенной координате; s- число обобщенных координат в механической системе. Если для исследуемой системы были составлены дифференциальные уравнения движения в форме уравнений Лагранжа II - го рода, то для определения возможных положений равновесия достаточно приравнять обобщенные силы нулю и решить полученные уравнения относительно обобщенных координат. Если механическая система находится в равновесии в потенциальном силовом поле, то из уравнений (1) получаем следующие условия равновесия:
Следовательно, в положении равновесия потенциальная энергия имеет экстремальное значение. Не всякое равновесие, определяемое вышеприведенными формулами, может быть реализовано практически. В зависимости от поведения системы при отклонении от положения равновесия говорят об устойчивости или неустойчивости данного положения. Виды равновесия: Устойчивое: При малом отклонении тела от положения равновесия возникает сила, стремящаяся возвратить тело в исходное состояние. Безразличное: При малом отклонении тело остается в равновесии. Неустойчивое: При малом отклонении тела из положения равновесия возникают силы, стремящиеся увеличить это отклонение. В положении устойчивого равновесия тело обладает минимальной потенциальной энергией. При выведении тела из этого положения его потенциальная энергия увеличивается. Если работу над телом совершает только сила тяжести, то в положении устойчивого равновесия центр тяжести тела находится на наименьшей высоте. Все тела стремятся к минимуму потенциальной энергии. (Потенциальная яма). Равновесие тел на опоре: линия действия силы тяжести проходит через площадь опоры (Пизанская башня). Чем ниже центр тяжести, тем более устойчиво равновесие Билет 7 Вопрос 1 Если голономная механическая система описывается лагранжианом
где i = 1, 2, … n (n — число степеней свободы механической системы). Лагранжиан представляет собой разность кинетической и потенциальной энергий системы. Если в системе действуют непотенциальные силы (например, силы трения), уравнения Лагранжа второго рода имеют вид
где Такие уравнения можно составить, рассматривая изменение каждой из обобщенных координат. Число уравнений Лагранжа определяется числом степеней свободы системы. Уравнения, по сути, являются алгоритмом получения дифференциальных уравнений движения точки, тела или системы тел в тех обобщенных координатах, которые выбраны исследователем. Для применения этого алгоритма необходимо: 1) уметь определять кинетическую энергию системы тел, как функцию обобщенных скоростей, 2) уметь определять виртуальную работу сил на каждом из рассматриваемых возможных перемещений 3) уметь выполнять стандартные, и весьма простые, математические операции с получаемыми выражениями. По сравнению с ур-ниями в декартовых координатах (см., напр., ур-ния Лагранжа 1-го рода) ур-ние обладает тем важным преимуществом, что число их равно числу степеней свободы системы и не зависит от кол-ва входящих в систему материальных частиц или тел; кроме того, при идеальных связях из ур-ний (3) автоматически исключаются все наперёд неизвестные реакции связей. Л. у. 2-го рода, дающими весьма общий и притом достаточно простой метод решения задач, широко пользуются для изучения движения разл. механич. систем, в частности в динамике механизмов и машин, в теории гироскопа ,в теории колебаний и др. Вопрос 2 Принцип Даламбера для материальной точки
По теореме Пуансо систему сил инерции, приложенных к точкам твердого тела, в общем случае можно заменить силой и парой сил. Сила приложена в центре приведения и равна главному вектору сил инерции, момент пары равен главному моменту сил инерции относительно центра приведения. Поскольку Тогда с учетом теоремы об изменении кинетического момента в поступательно движущейся с центром масс системе отсчета Рассмотрим частные случаи движения твердого тела. 1) При поступательном движении твердого тела выбирая за центр приведения центр масс системы, находим, что главный момент сил инерции относительно центра масс равен нулю
То есть система сил инерции приводится к равнодействующей, которая приложена в центре масс и определяется равенством 2) При вращении тела, имеющего плоскость материальной симметрии, вокруг оси, проходящей через центр масс перпендикулярно этой плоскости выбирая за центр приведения неподвижную точку (рис. 17.3), совпадающую с центром масс, находим, что
3) При плоском движении твердого тела, имеющего плоскость материальной симметрии в качестве центра приведения выбираем центр масс, расположенный в плоскости симметрии тела, которая перемещается в координатной плоскости 4) Аналогично рассматривается приведение системы сил инерции при вращении тела, имеющего плоскость материальной симметрии, вокруг оси, не проходящей через центр масс. При этом за центр приведения может выбираться как центр масс, так и неподвижная точка на оси вращения (рис. 17.5). Если в качестве центра приведения принимается точка где Билет 8 Вопрос 1 Дифференциальные ур-ния поступательного движения твердого тела: Вопрос 2 Сформулировать записанное можно следующим образом. В любой момент движения механической системы с идеальными связями сумма виртуальных работ активных сил и сил инерции на любом возможном перемещении системы равна нулю. Это равенство принято называть общим уравнением динамики или принципом Лагранжа-Даламбера. для уравновешенной системы сил уже в соответствии с принципом возможных перемещений сумма виртуальных работ сил на любом возможном перемещении системы должна быть равна нулю.
Билет 9 Вопрос 1 Дифф-ные ур-ния вращения твердого тела вокруг неподвижной оси: Вопрос 2
Поиск по сайту: |


 (1)
(1) (2)
(2)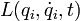 (
(  — обобщённые координаты, t — время, точкой обозначено дифференцирование по времени) и в системе действуют только потенциальные силы, то уравнения Лагранжа второго рода имеют вид
— обобщённые координаты, t — время, точкой обозначено дифференцирование по времени) и в системе действуют только потенциальные силы, то уравнения Лагранжа второго рода имеют вид

 — кинетическая энергия системы,
— кинетическая энергия системы,  — обобщённая сила.
— обобщённая сила.
 ,
,  , применяя теорему о движении центра масс и теорему об изменении кинетического момента, находим:
, применяя теорему о движении центра масс и теорему об изменении кинетического момента, находим:  ,
,  . Здесь за центр приведения
. Здесь за центр приведения  принята произвольная неподвижная точка в инерциальной системе отсчета. Обычно за центр приведения выбирается центр масс механической системы.
принята произвольная неподвижная точка в инерциальной системе отсчета. Обычно за центр приведения выбирается центр масс механической системы. ,
,  .
. .
. .
. . Система сил приводится к паре сил, лежащей в плоскости материальной симметрии тела. Вектор момента этой пары определяется равенством
. Система сил приводится к паре сил, лежащей в плоскости материальной симметрии тела. Вектор момента этой пары определяется равенством  . Алгебраический момент пары сил инерции может быть вычислен по формулам:
. Алгебраический момент пары сил инерции может быть вычислен по формулам:
 .
. (рис. 17.4). Так как плоское движение может быть представлено как сложение поступательного движения с центром масс и вращательного вокруг оси
(рис. 17.4). Так как плоское движение может быть представлено как сложение поступательного движения с центром масс и вращательного вокруг оси  , проходящей через центр масс, то система сил инерции приводится к силе и к паре, лежащей в плоскости материальной симметрии
, проходящей через центр масс, то система сил инерции приводится к силе и к паре, лежащей в плоскости материальной симметрии  ,
,  , где
, где  − момент инерции относительно оси, проходящей через центр масс, перпендикулярно плоскости материальной симметрии.
− момент инерции относительно оси, проходящей через центр масс, перпендикулярно плоскости материальной симметрии. , лежащая на оси вращения в плоскости симметрии, то главный момент сил инерции равен
, лежащая на оси вращения в плоскости симметрии, то главный момент сил инерции равен  ,
, - момент инерции тела относительно оси вращения
- момент инерции тела относительно оси вращения  .
. и т.д.
и т.д.  – проекция внешней силы. Все точки тела движутся так же, как и его центр масс С. Для осуществления поступательного движения необходимо, чтобы главный момент всех внешних сил относительно центра масс был равен 0:
– проекция внешней силы. Все точки тела движутся так же, как и его центр масс С. Для осуществления поступательного движения необходимо, чтобы главный момент всех внешних сил относительно центра масс был равен 0:  =0.
=0.
 , Jz – момент инерции тела относительно оси вращения z,
, Jz – момент инерции тела относительно оси вращения z,  – момент внешних сил относительно оси вращения (вращающий момент).
– момент внешних сил относительно оси вращения (вращающий момент).  , e – угловое ускорение, чем больше момент инерции при данном
, e – угловое ускорение, чем больше момент инерции при данном  .
.