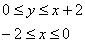|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Если интегрирование проводится по «игрек», то переменная «икс» считается константой. И наоборот ⇐ ПредыдущаяСтр 7 из 7
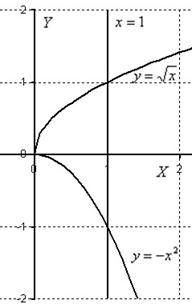
Тем не менее, вот нашли вы первообразную Момент второй, подстановка пределов интегрирования. По стандартной формуле Ньютона-Лейбница сначала вместо «игреков» мы подставили И, наконец, может показаться странным результат: 2) Берём оставшийся внешний интеграл: При нахождении интеграла Ответ: Пример 6 Вычислить двойной интеграл Это пример для самостоятельного решения. В образце решения, как и в разобранном примере, использован первый способ обхода области. На практике немало примеров, где трудно (а то и невозможно) обойтись без микрокалькулятора-«дробовика». Рассмотрим практический пример на данную тему: Пример 7 Вычислить двойной интеграл по области Задача будет решена двумя способами, так как готовое решение у меня уже есть =) А если серьезно, второй способ будет нужен для дополнительных важных комментариев. Решение: Изобразим область интегрирования на чертеже:
Область интегрирования тут простая, и основной гемор ожидается как раз в вычислениях. Выберем следующий порядок обхода области: 1) Начинающим чайникам всегда рекомендую выполнять проверку, особенно в подобных примерах: возьмите частную производную по «игрек» от первообразной Будьте предельно внимательны в подстановке пределов интегрирования: сначала вместо«игреков» подставляем 2) Второй шаг прост: Перейдём к обратной функции
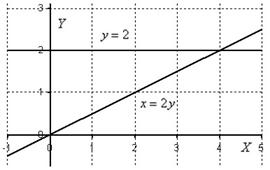
Таким образом: 1) Вычислим внутренний интеграл: Когда мы интегрируем по «икс», то переменная «игрек» считается константой. Не лишней будет и промежуточная проверка, возьмём частную производную по «икс» от найденной первообразной: Подстановка пределов интегрирования здесь сложнее: сначала вместо «иксов» подставляем 1, затем вместо «иксов» подставляем Степени рекомендую оставить в виде 2) Результаты совпали, как оно и должно быть. Легко заметить, что первый способ решения был заметно проще. Дроби в рассмотренном примере еще худо-бедно можно привести к общему знаменателю вручную. Но не удивляйтесь, если на практике получится ответ вроде Ответ: Ответ получился отрицательным. Геометрически это обозначает, что график подынтегральной функции Пример 8 Вычислить двойной интеграл по области Это пример для самостоятельного решения. Ответ будет целым – чтобы от своего хорошего настроения не запугать вас окончательно =). Похожие двойные интегралы встречаются в известном задачнике Кузнецова, и по этой причине пример тоже уместен. Полное решение и ответ в конце урока. Студенты-заочники почти всегда сталкиваются с двойными интегралами наподобие тех, которые уже рассмотрены, но никто не застрахован от творческих примеров, где в подынтегральной функции есть какие-нибудь синусы, косинусы, экспоненты и т.п. Рассмотрим заключительные примеры на данную тему: Пример 9 Вычислить двойной интеграл по области Решение: В ходе выполнения чертежа может возникнуть трудность с построением прямой Выполним чертёж:
После выполнения чертежа нужно выяснить, какой порядок обхода области выгоднее применить. Рассмотрим первый способ обхода: Очевидно, что первый способ является крайне неудачным, поскольку внутренний интеграл Но есть еще и второй способ обхода области: Выглядит гораздо привлекательнее, начинаем вычисления: 1) По формуле Ньютона-Лейбница разберемся с внутренним интегралом: Когда мы интегрируем по «икс», то переменная «игрек» считается константой. Если возникают трудности с интегрированием, можно прибегнуть даже к такому способу: временно замените «игрек» конкретным числом, например, «пятёркой»: И, конечно же, лучше сделать проверку, продифференцировав первообразную по «икс»: Далее при подстановке пределов интегрирования сначала вместо «икса» подставляем 2) Полученный результат
Второй интеграл взят методом подведения функции под знак дифференциала. Ответ: Таким образом, выбор порядка обхода иногда зависит не только от самой области интегрирования, но и от подынтегральной функции. Пример 10 Вычислить двойной интеграл по области Это пример для самостоятельного решения. Хочется привести ещё примеры, но в первом раунде я обещал не маньячить, поэтому скрепя сердце, заканчиваю статью. Множество других примеров на вычисление двойных интегралов можно найти в соответствующем архиве на странице Готовые решения по высшей математике. Если тема проработана качественно, то рискну предположить, что многие читатели самостоятельно смогут разобраться и в тройных интегралах – принципы решения очень похожи! Решения и ответы: Пример 2: Решение: Изобразим область Пример 4: Решение: Изобразим область интегрирования на чертеже. Пример 6: Решение: Изобразим область интегрирования на чертеже: Пример 8: Решение: Изобразим область интегрирования на чертеже: Пример 10: Решение: Изобразим область интегрирования на чертеже:
Поиск по сайту: |
 и возникли сомнения, а правильно ли она найдена? Всегда можно выполнить проверку, в данном случае следует найти частную производную по «игрек»:
и возникли сомнения, а правильно ли она найдена? Всегда можно выполнить проверку, в данном случае следует найти частную производную по «игрек»:
 , а затем – нижний предел интегрирования (нули). После подстановки должны остаться только «иксы».
, а затем – нижний предел интегрирования (нули). После подстановки должны остаться только «иксы».

 использован метод подведения функции под знак дифференциала. Где-нибудь возникли сомнения в правильности интегрирования? Возьмите производную по «икс» и выполните проверку!
использован метод подведения функции под знак дифференциала. Где-нибудь возникли сомнения в правильности интегрирования? Возьмите производную по «икс» и выполните проверку!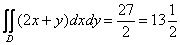
 ,
, 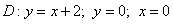





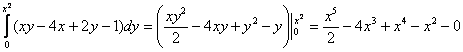
 и получите подынтегральную функцию
и получите подынтегральную функцию  .
. , затем – ноль. В оформлении вполне допустимо записать один, а не несколько нолей, как это сделано в данном примере. После подстановки должны остаться только «иксы».
, затем – ноль. В оформлении вполне допустимо записать один, а не несколько нолей, как это сделано в данном примере. После подстановки должны остаться только «иксы».
 и изменим порядок обхода области:
и изменим порядок обхода области:



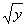 . После подстановки должны остаться только «игреки».
. После подстановки должны остаться только «игреки». , а не преобразовывать их в корни – будет удобнее интегрировать на втором шаге:
, а не преобразовывать их в корни – будет удобнее интегрировать на втором шаге: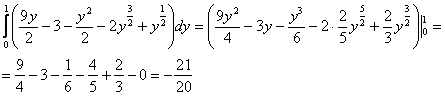
 , по крайне мере, в своей коллекции я нашел немало диких примеров, где без микрокалькулятора-«дробовика» фактически не обойтись.
, по крайне мере, в своей коллекции я нашел немало диких примеров, где без микрокалькулятора-«дробовика» фактически не обойтись.
 (поверхность в пространстве) полностью или бОльшей частью (не проверял) располагается ниже области интегрирования
(поверхность в пространстве) полностью или бОльшей частью (не проверял) располагается ниже области интегрирования  под плоскостью
под плоскостью  .
.
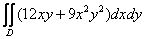

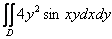
 , которая параллельна оси
, которая параллельна оси  . Ничего сложного: если
. Ничего сложного: если  , то
, то 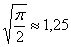 – примерно на этом уровне и следует провести прямую.
– примерно на этом уровне и следует провести прямую.


 придётся дважды брать по частям.
придётся дважды брать по частям.

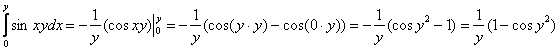
 .
.

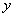 , затем – ноль. После подстановки должны остаться только «игреки».
, затем – ноль. После подстановки должны остаться только «игреки». перемещаем во внешний интеграл, не забывая, что там уже есть
перемещаем во внешний интеграл, не забывая, что там уже есть  и константа 4:
и константа 4:

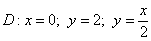










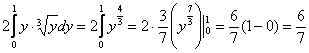




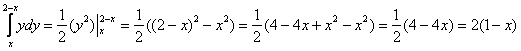 ;
;