|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Двойной интеграл как объем тела
Рассмотрим основной геометрический смысл двойного интеграла Геометрически функция двух переменных Тогда двойной интеграл численно равен объёму цилиндрического бруса Что такое цилиндрический брус, думаю, всем понятно из чертежа. Плоская фигура Дополнительно поясню геометрический смысл на Примере 1. В нём мы рассматривали двойной интеграл Подынтегральная функция Двойной интеграл может быть и отрицательным, в таких случаях график функции Прошу прощения, пока не подыскал программы для построения трехмерных чертежей, которая бы меня устраивала, пришлось объяснять на пальцах. Однако на практике почти всегда встречаются задачи на формальное вычисление двойных интегралов, поэтому мы продолжим совершенствовать технику вычислений: Пример 3 Вычислить двойной интеграл Решение: Изобразим область интегрирования на чертеже: После того, как корректно выполнен чертеж и правильно найдена область интегрирования, самое время разобраться с порядком обхода. Согласно первому способу обхода, область придется разделить на две части, при этом необходимо будет вычислить следующие интегралы: Энтузиазма, прямо скажем, мало. Проанализируем, а не проще ли использовать второй способ обхода области? Перейдем к обратным функциям, переход здесь элементарен: Порядок обхода области: Таким образом: Ну вот, совсем другое дело. И снова заметьте, что во внутреннем интеграле интегрирование осуществляется по «икс», поэтому константу 1) Найдём внутренний интеграл: Всё-таки подстановка пределов интегрирования, порой, выглядит своеобразно. Сначалавместо «икса» мы подставили верхний предел интегрирования 2) Результат предыдущего пункта подставим во внешний интеграл, при этом не забываем про
Ответ: Для тренировки можете попробовать вычислить двойной интеграл менее рациональным способом: Пример 4 Вычислить двойной интеграл Это пример для самостоятельного решения. Постройте область Усложняем задачу, теперь подынтегральная функция будет представлять собой сумму. Рассмотрим еще два примера, где я остановлюсь на приёме вычисления интеграла, который типичен и эффективен для кратных интегралов: Пример 5 Вычислить двойной интеграл Решение: Сначала рассмотрим то, чего делать не нужно – в данном случае не следует использовать свойства линейности кратного интеграла и представлять его в виде: Решение, как обычно, начинаем с построения области интегрирования: Область Таким образом: Здесь, в отличие от двух предыдущих примеров, из внутреннего интеграла ничего вынести нельзя, поскольку начинкой является сумма. С повторными интегралами опять разбираемся по отдельности. Да, кстати, кто хочет посмотреть, как решать повторные интегралы одной строкой, пожалуйста, зайдите на страницу Готовые решения по высшей математике и закачайте архив с примерами решений кратных интегралов. 1) Сначала берём внутренний интеграл: Хотелось бы остановиться на нескольких существенных моментах. Во-первых, о частном интегрировании. О нём я уже подробно рассказывал в статье Дифференциальные уравнения в полных дифференциалах. Вкратце повторюсь:
Поиск по сайту: |
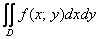 . Предполагаем, что функция
. Предполагаем, что функция  существует в каждой точке
существует в каждой точке  плоской области
плоской области  .
. , то есть поверхность располагается над плоскостью
, то есть поверхность располагается над плоскостью  .
. :
:
 , причём область интегрирования имела следующий вид:
, причём область интегрирования имела следующий вид:
 задаёт плоскость в пространстве. Из начала координат перпендикулярно экрану монитора мысленно проведите на себя стрелку оси
задаёт плоскость в пространстве. Из начала координат перпендикулярно экрану монитора мысленно проведите на себя стрелку оси 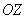 . В данном примере плоскость
. В данном примере плоскость  располагается в пространстве над областью
располагается в пространстве над областью  . Возможно, не всем до конца понятно, о каком объеме идёт речь: из границы области
. Возможно, не всем до конца понятно, о каком объеме идёт речь: из границы области  ,
, 


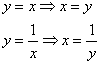


 можно сразу вынести во внешний интеграл
можно сразу вынести во внешний интеграл
 , затем вместо «икса» подставили нижний предел интегрирования
, затем вместо «икса» подставили нижний предел интегрирования  . Будьте внимательны при подстановках!
. Будьте внимательны при подстановках!

 . Результаты должны совпасть.
. Результаты должны совпасть. ,
, 
 ,
,