 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Прискорення - це векторна фізична величина, що дорівнює відношенню зміни швидкості до часу, протягом якого ця зміна відбулася
Якщо швидкість за будь-які однакові проміжки часу збільшується на ту саму величину, то такий рух називається рівноприскореним. Якщо швидкість тіла зменшується згодом на ту саму величину, то рух називають рівносповільненим. У цілому рівнозмінним називають такий рух тіла, за якого прискорення є сталим ( Якщо рівнозмінний рух прямолінійний, то за одну з осей координат (наприклад, Ох) зручно взяти пряму, по якій рухається матеріальна точка, а за її додатний напрям - напрям початкової швидкості
Проекція вектора прискорення буде мати знак "+", якщо напрям вектора прискорення збігається з напрямом вектора 2. Графіки залежності кінематичних величин від часу. Для побудови графіка прискорення прямолінійного рівнозмінного руху по осі ординат відкладають прискорення, а по осі абсцис - час. Оскільки під час рівнозмінного руху прискорення не змінюється, то графік прискорення є прямою, паралельною осі часу. На рис.2.1.16 показано графік прискорення прямолінійного рівноприскореного руху I (а = 2 м/с2) і рівносповільненого II (а = - 4 м/с2).
Із формули (2.1.8) легко визначити миттєву швидкість прямолінійного рівноприскореного руху: Швидкість рівнозмінного руху є лінійною функцією часу. Із формули (2.1.10) знайдемо значення проекції вектора швидкості на вісь Ох: Характерні графіки швидкості рівнозмінного руху матеріальної точки для різних випадків показано на рис.2.1.17, на якому: а - графік швидкості рівноприскореного руху без початкової швидкості; б - графік швидкості рівноприскореного руху з початковою швидкістю; в - графік швидкості рівносповільненого руху. В усіх випадках графіки швидкості прямолінійного рівнозмінного руху мають вигляд прямих ліній, проведених під кутом до осі часу. Використовуючи формулу (2.1.10) варто мати на увазі, що напрям однієї з осей системи відліку збігається з напрямом вектора початкової швидкості Середню скалярну швидкість рівнозмінного руху можна знайти як середнє арифметичне початкової Якщо відомі час і середня скалярна швидкість, то шлях, пройдений матеріальною точкою за рівнозмінного руху, Після підстановки значення середньої швидкості (2.1.11) у рівняння (2.1.12) одержуємо Підставляючи замість Рівняння (2.1.13) можна одержати іншим способом на підставі графіка швидкості рівноприскореного руху з початковою швидкістю (рис.2.1.18). На цьому графіку пройдений шлях чисельно дорівнює площі трапеції, яку можна подати як суму площ прямокутника і трикутника (на рис.2.1.13 заштриховані). Таким чином, числове значення шляху рівноприскореного руху: Площа прямокутника дорівнює добутку основи t на висоту Площа трикутника дорівнює половині добутку основи t на висоту
Додаючи площі Sпр і Sтр, знаходять вираз для шляху рівнозмінного руху у вигляді рівняння (2.1.13) Якщо тіло рухається рівноприскорено без початкової швидкості (υ=0), то пройдений шлях: Таким чином, шлях, пройдений тілом у рівнозмінному русі, є квадратичною функцією часу і завжди додатною величиною. Графіки шляху для різних видів прямолінійного рівнозмінного руху показано на рис.2.1.19: І - рівноприскореного руху з початковою швидкістю; ІІ - рівноприскореного руху без початкової швидкості; ІІІ - рівносповільненого руху. Графіки шляху І і ІІ прямолінійного рівноприскореного руху є гілками парабол, вершини яких знаходяться в початку координат. У першому випадку крива піднімається крутіше, тобто з двох тіл, що рухаються з однаковими прискореннями,
Графік шляху ІІІ рівносповільненого руху показано до моменту часу Графік цього шляху показано пунктирною лінією (рис.2.1.19). Він подібний до графіка шляху ІІ, але вершина його гілки параболи виходить не із початку осей координат, а з точки, де відбулася зміна напряму руху. Із формули (2.1.13) для проекції переміщення під час рівноприскореного руху знаходимо: Для знаходження координати X точки в будь-який момент часу t потрібно до початкової координати X0 додати проекцію вектора переміщення на вісь Ох (рис.2.1.20):
З виразів (2.1.14) і (2.1.15) дістаємо: Вираз (2.1.16) називають рівнянням рівнозмінного прямолінійного руху (кінематичний закон цього руху). Права частина формули (2.1.16) є алгебраїчною сумою, оскільки X0,
Отже, основними рівняннями, що описують прямолінійний рівнозмінний рух точки, є рівняння (2.1.8), (2.1.10), (2.1.13) і (2.1.16). У цих рівняннях у разі рівносповільненого руху прискорення від'ємне. Якщо з формули (2.1.9) визначити значення t і підставити його в (2.1.13), то після перетворень дістанемо рівняння прямолінійного рівнозмінного руху такого вигляду: Якщо прямолінійний рівноприскорений рух тіла починається зі стану спокою( або Формули (2.1.17) - (2.1.19) часто використовують для розв'язання задач. Запитання для самоперевірки 1. Що таке прискорення і для чого його потрібно знати? 2. Під час будь-якого нерівномірного руху швидкість змінюється. Як характеризує цю зміну прискорення? 3. Чим відрізняється сповільнений прямолінійний рух від прискореного? 4. Що таке рівноприскорений рух? 5. Чи може тіло рухатися з великою швидкістю, але з малим прискоренням? 6. Як напрямлений вектор прискорення у разі прямолінійного руху? 7. Швидкість - векторна величина і може змінюватися як модуль швидкості, так і напрям вектора швидкості. Що саме змінюється під час прямолінійного рівноприскореного руху? 8. Чи може швидкість руху тіла дорівнювати нулю, коли його прискорення не дорівнює нулю? 9. Як можна вивести формули швидкості та шляху рівнозмінного руху? 10. Що називають миттєвою швидкістю змінного руху?
Поиск по сайту: |
 ).
). . Тоді прискорення обчислюють як скалярну величину - проекцію вектора прискорення - і формулу (2.1.8) можна записати в скалярній формі:
. Тоді прискорення обчислюють як скалярну величину - проекцію вектора прискорення - і формулу (2.1.8) можна записати в скалярній формі:



 . Якщо вектор прискорення
. Якщо вектор прискорення  спрямовано протилежно вектору
спрямовано протилежно вектору  у деякий момент часу може виявитися від'ємним. Це означає, що швидкість
у деякий момент часу може виявитися від'ємним. Це означає, що швидкість 

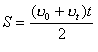 .
.


 .
. :
: . З огляду на те, що
. З огляду на те, що  , одержують:
, одержують:  .
. .
. .
. , раніше пройде заданий шлях те тіло, початкова швидкість якого більша. За графіком шляху рівноприскореного руху можна визначити швидкість руху точки.
, раніше пройде заданий шлях те тіло, початкова швидкість якого більша. За графіком шляху рівноприскореного руху можна визначити швидкість руху точки.
 , коли швидкість змінює свій знак на протилежний (за умови, що до зупинки і після неї прискорення за модулем і напрямом залишається сталим). Коли зміниться напрям руху на протилежний початковому, шлях можна обчислити за формулою
, коли швидкість змінює свій знак на протилежний (за умови, що до зупинки і після неї прискорення за модулем і напрямом залишається сталим). Коли зміниться напрям руху на протилежний початковому, шлях можна обчислити за формулою  .
. .
.

 , ax можуть бути додатними і від'ємними. Можливі залежності координати від часу у разі рівнозмінного руху зображено на рис.2.1.21.
, ax можуть бути додатними і від'ємними. Можливі залежності координати від часу у разі рівнозмінного руху зображено на рис.2.1.21.

 ), то рівняння (2.1.17) набуває вигляду
), то рівняння (2.1.17) набуває вигляду 
 .
.