 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вправи на застосування таблиць інтегралів
Після розгляду наведених нижче прикладів рекомендується переписати їх умови і розв’язати самостійно, записуючи по памяті необхідну для цього формулу.
I. Інтеграли вигляду
Довідка. При інтегруванні степеневих функцій приходиться добуток і частку різних степенів змінної 1. 3. 5. 8. В співвідношеннях 6) - 9) Зауваження. Нижче будуть використовуватись скорочення при посиланні на таблиці, наприклад,Т3(7) : таблиця 3 (формула 7) , або посилання на довідку, наприклад,Д9 : довідка (формула 9).
II. Інтеграли вигляду
.
III. Інтеграли вигляду
IV. Інтеграли вигляду
V. Інтеграли вигляду
Приклади. Користуючись властивостями та таблицями 1-3, знайти інтеграли. Результати перевірити за допомогою дифереціювання.
В прикладах 58-73 підінтегральні вирази зводяться до табличних після додаткових перетворень
Інтегрування частинами
Теорема. Нехай функції U=U(x) i V=V(x) диференційовні на деякому інтервалі (a, b), тоді на (a, b) виконується рівність
Доведення.Із власивостей диференціала відомо:
Перейшовши до інтегралів, отримаємо рівність (1). Приклад 1. Інтегруємо частинами за формулою (1)
Візьмемо
Приклад 2.
Із наведених прикладів бачимо, що складність інтегрування залежить від вдалого розподілу підінтегрального виразу на два співмножники Так, наприклад в інтегралах В інтегралах
Приклади. Знайти інтеграли.
Відповіді: 1. 2. 3. 4. 6. 8. 9. 10. 11. 12. 13. 14. 15.
Поиск по сайту: |

 зводити до одного степеня з раціональним показником :
зводити до одного степеня з раціональним показником : 2.
2. 
 4.
4. 
 6.
6.  7.
7. 
 9.
9. 
 - натуральне,
- натуральне,  - ціле, а в співвідношеннях 1) - 4)
- ціле, а в співвідношеннях 1) - 4)  - довільні дійсні числа.
- довільні дійсні числа.





 .
.













 .
.































 .
. .
. .
. .
. .
. .
. .
. .
. .
.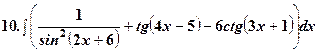 .
. .
. .
. .
. .
. .
. .
. .
.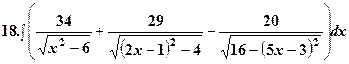 .
. .
.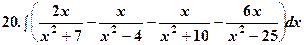 .
. .
. .
.













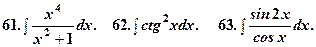
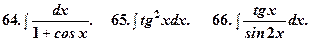



 (1)
(1) .
.


 , тоді
, тоді

 і
і  . В окремих випадках функція
. В окремих випадках функція  ,то
,то  і
і  - уже многочлен
- уже многочлен  - го степеня. Вираз для
- го степеня. Вираз для  повинен бути таким, щоб інтеграл від
повинен бути таким, щоб інтеграл від 


 потрібно вибрати
потрібно вибрати  , а за
, а за  тоді
тоді  знаходиться за таблицею інтегралів.
знаходиться за таблицею інтегралів.

 за
за  потрібно відповідно брати
потрібно відповідно брати  , тоді
, тоді  і
і  легко знаходиться інтегруванням.
легко знаходиться інтегруванням.














 .
. .
. .
. 5.
5. 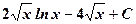 .
. . 7.
. 7.  .
. .
. .
. .
. .
. .
. .
. .
. . Вказівка. У чисельнику спочатку перетворити
. Вказівка. У чисельнику спочатку перетворити  , а тоді інтегрувати частинами.
, а тоді інтегрувати частинами.