 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
КИНЕМАТИКА КРИВОЛИНЕЙНОГО ДВИЖЕНИЯ ⇐ ПредыдущаяСтр 2 из 2
Эта тема будет посвящена более сложному виду движения – КРИВОЛИНЕЙНОМУ. Как несложно догадаться, криволинейным называется движение, траектория которого представляет собой кривую линию. И, поскольку это движение сложнее прямолинейного, то для его описания уже не хватает тех физических величин, которые были перечислены в предыдущей главе. Для математического описания криволинейного движения имеются 2 группы величин: линейные и угловые.
ЛИНЕЙНЫЕ ВЕЛИЧИНЫ. 1.Перемещение
поскольку в прямолинейном движении эти различия не играют принципиальной роли, да и
вой S. Но, имея дело с криволинейным движением, этот вопрос нужно прояснить. Итак, что такое путь (или расстояние)? – Это длина траектории движения. То есть, если Вы отследите траекторию движения тела и измерите ее (в метрах, километрах и т.д.), вы получите величину, которая называется путем (или расстоянием) S(см. рис.1.3). Таким образом, путь – это скалярная величина, которая характеризуется только числом.
точкой начала пути и точкой конца пути. И, поскольку перемещение имеет строгую направленность из начала
и характеризуется не только численным значением, но и направлением (рис.1.3). Нетрудно догадаться, что, если тело совершает движение по замкнутой траектории, то к моменту его возвращения в начальное положение перемещение будет равно нулю (см. рис.1.4). 2. Линейная скорость
Рис.1.5
О1
90°
О2
криволинейной траектории тела. Любая кривая линия представляет собой соединение между собой дуг разных окружностей. На рис.1.5 изображены только две из них: окружность (О1, r1) и окружность (О2, r2). На момент прохождения тела по дуге данной окружности ее центр становится временным центром поворота с радиусом, равным радиусу этой окружности. Вектор, проведенный из центра поворота в точку, где в данный момент находится тело, называется радиусом-вектором. На рис.1.5 радиусы-векторы представлены векторами при криволинейном движении всегда есть ускорение! (Даже если движение осуществляется с постоянной линейной скоростью.) Причем, ускорение, о котором идет речь в данном случае, в дальнейшем мы будем называть линейным ускорением. 3. Линейное ускорение
О
изображено тело, движущееся по круговой траектории с центром поворота в точке О. Ускорение, которое изменяет направление вектора Ускорение, которое изменяет модуль вектора • если линейная скорость • если линейная скорость направлены. Таким образом, эти два ускорения всегда образуют между собой прямой угол (90º) и являются составляющими полного линейного ускорения
Замечу, что в данном случае речь идет именно о векторной сумме, но ни в коем случае не о скалярной. Чтобы найти численное значение
Отсюда следует:
По каким формулам рассчитывать
УГЛОВЫЕ ВЕЛИЧИНЫ. 1. Угол поворота φ. При криволинейном движении тело не только проходит какой-то путь и совершает какое-то перемещение, но и поворачивается на определенный угол (см. рис. 1.7(а)). Поэтому для описания такого движения вводится величина, которая называется углом поворота, обозначается греческой буквой φ (читается «фи»). В системе СИ угол поворота измеряется в радианах (обозначается «рад»). Напомню, что один полный оборот равен 2π радианам, а число π есть константа: π ≈ 3,14. на рис. 1.7(а) изображена траектория движения тела по окружности радиуса r с цетром в точке О. Сам угол поворота – это угол между радиус-векторами тела в некоторые моменты времени. 2. Угловая скорость ω – это величина, показывающая, как изменяется угол поворота за единицу времени. (ω – греческая буква, читается «омега».) На рис. 1.7(б) изображено положение материальной точки, движущейся по круговой траектории с центром в точке О, через промежутки времени Δt. Если углы, на которые поворачивается тело в течение этих промежутков, одинаковы, то угловая скорость постоянна, и это движение можно считать равномерным. А если углы поворота разные – то движение неравномерное. И, поскольку угловая скорость показывает, на сколько радиан повернулось тело за одну секунду, то ее единица измерения – радиан в секунду (обозначается «рад/с»).
а). б). Δt Δt
О φ О Δt
3. Угловое ускорение ε – это величина, показывающая, как изменяется за единицу времени. И, поскольку угловое ускорение ε появляется тогда, когда изменяется , угловая скорость ω, то можно сделать вывод, что угловое ускорение имеет место только в случае неравномерного криволинейного движения. Единица измерения углового ускорения – «рад/с2» (радиан за секунду в квадрате). Таким образом, таблицу 1.1 можно дополнить еще тремя величинами: Табл.1.2
Теперь можно перейти непосредственно к рассмотрению всех видов криволинейного движения, а их всего лишь три:
Поиск по сайту: |
 . В разделе 1.1 мы не стали уточнять различие между понятием
. В разделе 1.1 мы не стали уточнять различие между понятием Рис.1.3 пути (расстояния) и понятием перемещения,
Рис.1.3 пути (расстояния) и понятием перемещения, Рис.1.4 А перемещение
Рис.1.4 А перемещение  пути в его конец, то оно является величиной векторной
пути в его конец, то оно является величиной векторной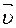 . В разделе 1.1 мы давали определение этой величины, и оно остается в силе, хотя тогда мы не уточняли, что эта скорость линейная. Как же направлен вектор линейной скорости? Обратимся к рис.1.5. Здесь изображен фрагмент
. В разделе 1.1 мы давали определение этой величины, и оно остается в силе, хотя тогда мы не уточняли, что эта скорость линейная. Как же направлен вектор линейной скорости? Обратимся к рис.1.5. Здесь изображен фрагмент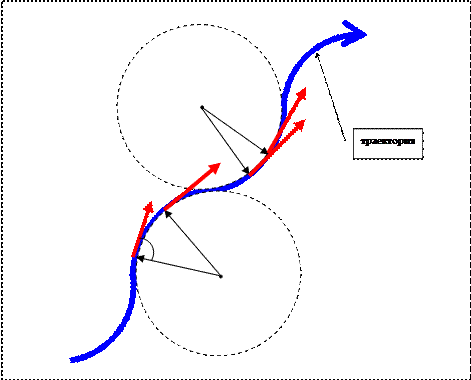



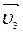


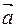 . Напомню, что ускорение возникает тогда, когда изменяется скорость. Соответственно, линейное ускорение появляется в случае изменения линейной скорости. А линейная скорость при криволинейном движении может изменяться кок по модулю, так и по направлению. Таким образом, полное линейное ускорение раскладывается на две составляющие, одна из которых влияет на направление вектора
. Напомню, что ускорение возникает тогда, когда изменяется скорость. Соответственно, линейное ускорение появляется в случае изменения линейной скорости. А линейная скорость при криволинейном движении может изменяться кок по модулю, так и по направлению. Таким образом, полное линейное ускорение раскладывается на две составляющие, одна из которых влияет на направление вектора  рис. 1.6
рис. 1.6

 .
. (1.8).
(1.8).

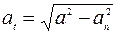 (1.9).
(1.9). рис. 1.7
рис. 1.7