 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
КИНЕМАТИКА ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯСтр 1 из 2Следующая ⇒
I. ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ ТЕМА 1.1. «КИНЕМАТИКА ПРЯМОЛИНЕЙНОГО И КРИВОЛИНЕЙНОГО ДВИЖЕНИЯ» КИНЕМАТИКА ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ
В этой главе предстоит изучить самый простой вид движения – ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ. Прямолинейным называется движение, которое осуществляется вдоль прямой линии. Выражаясь научно, это движение, траектория которого представляет собой прямую линию. Любое физическое явление описывается посредством математических формул, в которых фигурируют физические величины. Поэтому необходимо оговорить эти самые физические величины, характеризующие движение, в том числе и прямолинейное. Таковыми являются: Таблица 1.1
Заметьте, что в таблице 1.1 умышленно не приводится определение времени, поскольку оно скорее философское, чем физическое. А для изучения этого раздела физики вполне достаточно бытового представления о времени. Таким образом, при помощи этих четырех величин описываются все виды прямолинейного движения. А их всего три:
Рассмотрим каждое из них. А начнем с самого простого – равномерного прямолинейного движения. 1. Равномерное прямолинейное движение – это движение с постоянной скоростью. Если скорость тела не изменяется, то ускорения у него попросту нет. Математические признаки этого движения записываются следующим образом: υ=const, a=0. Попытаемся представить себе это движение: тело движется со скоростью, к примеру, 5 м/с, и, поскольку движение равномерное, его скорость не изменяется. Это означает, что за каждую секунду оно проходит расстояние в 5 метров. Как определить, какое расстояние пройдет это тело за время t = 20 секунд? Для этого нужно 5 м/с умножить на 20 с – получим расстояние S = 100 м. Таким образом, можем записать формулу равномерного прямолинейного движения: S = υt Отсюда легко вывести формулу скорости:
2. Равнопеременное движение – это движение с постоянным ускорением. В этом случае скорость все время изменяется, но изменяется равномерно: за каждую секунду на одну и ту же величину. Эта величина и равна ускорению тела. Например: тело движется с постоянным ускорением а = 2 м/с2. Если в определенный момент времени скорость тела равна, к примеру, 10 м/с, то в следующую секунду она увеличится на 2 м/с и будет равна 12 м/с, еще через секунду она увеличится еще на 2 м/с и станет равна уже 14 м/с – так каждую секунду. Получается равноускоренное движение. Но тело может двигаться так, что его скорость будет не увеличиваться, а наоборот уменьшаться. И в этом случае ускорение у тела тоже есть. Но, если в предыдущем примере оно было больше нуля ( а > 0 ), т.е. положительным, то при уменьшении скорости ускорение меньше нуля ( а < 0 ), т.е. считается отрицательным. Например: тело движется с постоянным ускорением а = - 2 м/с2. Если в определенный момент времени скорость тела равна, к примеру, 10 м/с, то в следующую секунду она уменьшится на 2 м/с и будет равна 8 м/с, еще через секунду она уменьшится еще на 2 м/с и станет равна уже 6 м/с – и, в конце концов, через 3 секунды тело остановится. Получается равнозамедленное движение. Правда слово «равнозамедленное» применять не принято, поэтому такое движение считается равноускоренным, но с отрицательным ускорением. А, в целом, движение с постоянным ускорением называется равнопеременным. Признаки равнопеременного движения можно записать следующим образом: υ ≠ const, a = const(a≠0). Математически равнопеременное движение описывается двумя уравнениями – уравнение пути и уравнение скорости, образующие систему:
где υ0 – начальная скорость тела (т.е. скорость в начале движения). 3. Неравнопеременное движение – это движение с изменяющимся ускорением. В случае этого движения все время изменяется не только скорость, но и ускорение. При чем изменяться они могут совершенно произвольно: могут все время увеличиваться или все время уменьшаться, а могут то увеличиваться, то уменьшаться. Но, как и в предыдущем случае, если скорость увеличивается, значит ускорение в это время положительное и сонаправлено со скоростью. А, если скорость уменьшается, то ускорение – отрицательное и направлено противоположно скорости (см. рис.1.1 и 1.2).
а > 0 Признаки неравнопеременного движения можно записать следующим образом: υ ≠ const, a ≠ const. Как видите, из всех прямолинейных движений этот вид – самый сложный. Но, тем не менее, и для него существуют формулы, позволяющие просчитывать все характеристики движения. Их тоже две: уравнение скорости и уравнение ускорения.
Символ « Обратите внимание, что формулы (1.1) и (1.4) отличаются лишь наличием символа дифференцирования. И неудивительно, ведь они описывают разновидности прямолинейного движения. И формулы (1.4) и (1.5) являются общими формулами для всех трех случаев прямолинейного движения. Возникает вопрос: как можно вычислить, например, S, руководствуясь этими формулами? – Для этого нужно совершить действие, обратное дифференцированию. А таковым является интегрирование. Проделаем это:
Из уравнения (1.4) имеем dS=υdt.
Чтобы избавиться от дифференциала в левой части равенства, необходимо это равенство проинтегрировать:
В левой части интеграл накладывается на дифференциал, и , поскольку эти действия взаимно обратные, они друг друга компенсируют, и величина S освобождается от дифференциала:
Аналогичную процедуру проделываем с формулой (1.5):
Таким образом, получаем еще две формулы для расчета прямолинейного неравнопеременного движения:
Все, о чем говорилось в этой главе, можно свести к простой таблице:
Таблица 1.2
Поиск по сайту: |
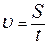 (1.1)
(1.1)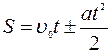 (1.2),
(1.2),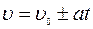 (1.3),
(1.3),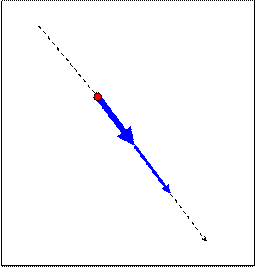 Рис. 1.1 Рис. 1.2
Рис. 1.1 Рис. 1.2 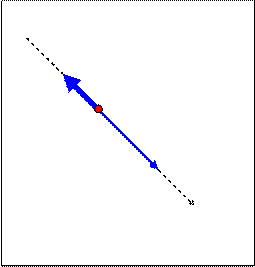
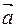
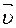

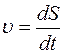 (1.4),
(1.4), 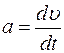 (1.5).
(1.5). » означает, что нужно выполнить действие дифференцирования по времени. Формально дифференцирование выполняется так же, как и взятие производной, только записывается в другой форме.
» означает, что нужно выполнить действие дифференцирования по времени. Формально дифференцирование выполняется так же, как и взятие производной, только записывается в другой форме. .
. .
.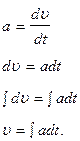
 (1.6)
(1.6) 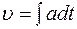 (1.7)
(1.7)