 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
КИНЕТИКА ГЕТЕРОГЕННЫХ РЕАКЦИЙ ⇐ ПредыдущаяСтр 2 из 2
Многие промышленные процессы основаны на реакциях, протекающих на границе раздела фаз. Такие процессы, как вы уже знаете, называются гетерогенными. Кинетика гетерогенных процессов характеризуется рядом особенностей, отличающих её от кинетики гомогенных процессов . Основное отличие - зависимость скорости гетерогенных от величинаыповерхности раздела фаз S. Скорость гетерогенных процессов обычно пропорциональна поверхности раздела; например, для реакции первого порядка A®B
Поверхность раздела фаз, а следовательно, и скорость процесса, могут быть увеличены дроблением твёрдых веществ или разбрызгиванием жидкости.
2. КИНЕТИКА СЛОЖНЫХ РЕАКЦИЙ( ОПУСКАЕМ ЗА НЕИМЕНИЕМ ВРЕМЕНИ)
ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА СКОРОСТЬ ХИМИЧЕСКИХ РЕАКЦИЙ
Уравнение Аррениуса Скорость реакции зависит не только от концентрации, но и от температуры. Как показывает опыт, скорость большинства реакций увеличивается при повышении температуры на 10° С в среднем в 2 Приближённой характеристикой зависимости скорости реакции от температуры является температурный коэффициент реакции γ: отношение константы скорости при температуре T + 10 к константе скорости при температуре T:
Считая γ приблизительно постоянным в интервале температур T2 – T1 , можно рассчитать kT2, зная величину kT1:
Это соотношение, называемое правилом Вант – Гоффа, может быть применимо лишь для приблизительных, ориентировочных расчётов. Однако для узкого интервала температур правило Вант – Гоффа часто бывает очень полезным. Расчёт показывает, что увеличение скорости реакции при повышении температуры не может быть объяснено лишь возрастанием числа столкновений. Это происходит потому, что не каждое столкновение частиц приводит к химической реакции. Лишь тогда, когда сталкивающиеся молекулы обладают определённой энергией, столкновение может быть эффективным и привести к химической реакции. Эти предположения были впервые высказаны С. Аррениусом. Согласно Аррениусу, к реакции приводит столкновение лишь тех молекул, энергия которых больше определённой величины Ea. Зависимость константы скорости реакции от температуры С. Аррениусом была представлена в виде
где k0 – предэкспоненциальный множитель, не зависящий от температуры; T – температура, К; R – газовая постоянная (R=8,14Дж·моль-1·град-1), Ea – энергия активации ( кДж/моль), равная разности между средней энергией молекул, способных к активным столкновениям, и средней энергией всех молекул. Как показывает опыт, величина энергии активации в достаточно широком интервале температур не зависит от температуры. Прологарифмируем уравнение (3.3):
или
Из (3.4, 3.5) следует метод экспериментального определения величины энергии активации: скорость реакции изучают при нескольких температурах, рассчитывают константы скорости для каждой температуры, строят график зависимости в координатах (ln k, 1/T). В этих координатах рассматриваемая зависимость линейная и тангенсом угла наклона равен – Ea/R (рис 3.1). Дифференцируя уравнение (3.4) по температуре, получим
Величина Ea/(RT2) > 0, поэтому логарифм константы скорости, а следовательно и сама константа и сама константа с температурой возрастают. Это, впрочем, видно и из (3.3). Из (3.6) видно также, что с возрастанием энергии активации (если мы, например, будем сравнивать несколько реакций с различными значениями Ea) значение
После интегрирования (3.6) от T1 до T2
или
(здесь 4,575 = 2,303 R, если R = 1,987 кал·моль-1·град-1). Из (3.8) можно определить величину энергии активации, если известны значения констант скорости при двух температурах T1 и T2. Заметим, что, поскольку экспериментальное определение константы скорости производится всегда с некоторой погрешностью, для более точного определения энергии активации обычно не ограничивается определением констант только при двух температурах.
Поиск по сайту: |
 .
.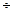 5 раза.
5 раза.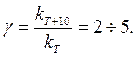 (3.1)
(3.1) . (3.2)
. (3.2) (3.3)
(3.3) (3.4)
(3.4) . (3.5)
. (3.5)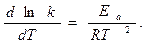 (3.6)
(3.6) будет также увеличиваться. Поэтому константа скорости реакции имеющей большую энергию активации. Будет возрастать с температурой быстрее.
будет также увеличиваться. Поэтому константа скорости реакции имеющей большую энергию активации. Будет возрастать с температурой быстрее.
 (3.7)
(3.7) (3.8)
(3.8)