 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Інтегрування частинами у визначеному інтегралі ⇐ ПредыдущаяСтр 2 из 2
Теорема 11. Якщо функції
Приклад.
Формули наближеного обчислення Визначений інтеграл від заданої неперервної функції далеко не завжди можна легко та точно обчислити. Однак, використовуючи геометричний зміст, можна побудувати ряд наближених формул, за допомогою яких інтеграл обчислюється з будь-якою точністю. Розглянемо такі формули. Нехай від заданої та неперервної на Поділимо Значення функції
Формули (7.15) та (7.16) називаються формулами лівого та правого прямокутників відповідно. Ця назва пов’язана з тим, що криволінійна трапеція наближено замінюється відповідною ступінчастою фігурою (рис. 7.8).
Рис. 7.8 ІІ. Формула трапецій. Більш точне значення визначеного інтеграла буде, якщо криву
Рис. 7.9 ІІІ. Формула Сімпсона. Поділимо
Рис. 7.10 замінюємо певною параболою. Таке наближення для обчислення визначеного інтеграла буде точнішим, ніж за попередніми формулами (рис. 7.10).
Обчислення площ плоских фігур Якою б не була криволінійна фігура, що обмежена неперервними кривими лініями, шляхом її розсікання лініями паралельними осям координат, обчислення площі фігури можна звести до обчислення площ розглянутих нижче фігур. І. Фігура обмежена лініями Якщо при виконанні всіх інших умов
ІІ. Фігура обмежена лініями
а якщо
ІІІ. Фігура обмежена лініями
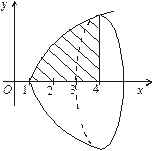
Рис. 7.14 Рис. 7.15 Приклад. Обчислити площу фігури, обмеженої лініями
Побудуємо фігуру, обмежену параболою
Точка Площа S фігури M1М8М2 за формулою (7.23) буде така:
Обчислення об’єму тіла Задача.Знаючи закон зміни площі поперечного перерізу тіла, знайти його об’єм. Розв’язання. Нехай функція Поділимо проміжок
Рис. 7.17 Тоді об’єм тіла наближено дорівнюватиме інтегральній сумі
якщо ця границя існує за (7.8). Задача.Знайти об’єм тіла Розглядаючи цю задачу, як частинний випадок попередньої задачі, встановлюємо, що площа поперечного перерізу
Зауваження.Аналогічно, об’єм тіла
Приклад. Обчислити об’єм тіла, утвореного обертанням навколо осі Ох фігури, обмеженої лініями l У прямокутній системі координат будуємо фігуру, обмежену даними лініями (рис. 7.19). За формулою (7.25) об’єм тіла буде таким: ЛІТЕРАТУРА 1. Бугров Я. С., Никольский С. М. Элементы линейной алгебры и аналитической геометрии. — М.: Наука, 1988. — 240 с. 2. Бугров Я. С., Никольский С. М. Дифференциальное и интегральное исчисление. — М.: Наука, 1988. — 432 с. 3. Бугров Я. С., Никольский С. М. Дифференциальные уравнения, интегралы, ряды, функции комплексного переменного. — М.: Наука, 1989. — 464 с. 4. Овчинников П. Ф., Яремчук Ф. П., Михайленко В. М. Высшая математика. — К.: Вища шк., 1987. — 552 с. 5. Пак В. В., Носенко Й. Л. Вища математика. — К.: Либідь, 1996. — 440 с. 6. Пискунов Н. С. Дифференциальное и интегральное исчисление. — Т. 1, 2. — М.: Наука, 1985. — 580 с., 602 с. 7. Збірник задач з вищої математики / За ред. Ф. С.Гудименка. — К.: КУ, 1967. — 352 с. 8. Клетеник Д. В. Сборник задач по аналитической геометрии. — М.: Наука, 1986. — 224 с. 9. Берман Г. Н. Сборник задач по курсу математического анализа. — М.: Наука, 1975. — 416 с. 10. Задачи и упражнения по математическому анализу (для вузов) / Под ред. Б. П. Демидовича. — М.: Наука, 1968. — 472 с. 11. Стрижак Т. Г., Коновалова Н. Р. Математический анализ. — К.: Либідь, 1995. — 240 с.
Поиск по сайту: |
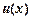 та
та  мають неперервні похідні для
мають неперервні похідні для 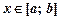 , то
, то (7.14)
(7.14)

 функції
функції 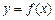 треба обчислити визначений інтеграл
треба обчислити визначений інтеграл 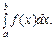
 .
.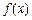 у точках
у точках  позначимо так:
позначимо так: 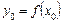 ,
, 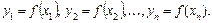 Побудуємо для функції
Побудуємо для функції  на проміжку
на проміжку 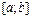 інтегральні суми, кожна з яких буде наближено подавати визначений інтеграл:
інтегральні суми, кожна з яких буде наближено подавати визначений інтеграл: (7.15)
(7.15)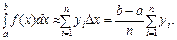 (7.16)
(7.16)
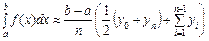 (7.17)
(7.17)
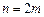 точками
точками 
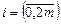 так, що а = х0, b = x2m. На кожному із цих проміжків криволінійну сторону трапеції, рівнянням якої є
так, що а = х0, b = x2m. На кожному із цих проміжків криволінійну сторону трапеції, рівнянням якої є 
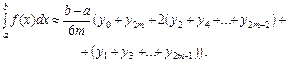 (7.18)
(7.18) Площа S такої криволінійної трапеції за геометричним змістом визначеного інтеграла така:
Площа S такої криволінійної трапеції за геометричним змістом визначеного інтеграла така:  .
. (рис. 7.12),
(рис. 7.12),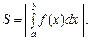 (7.20)
(7.20)
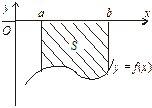

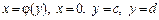 (рис. 7.13). Функція
(рис. 7.13). Функція 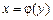 — неперервна та
— неперервна та 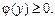 Площа S такої фігури буде
Площа S такої фігури буде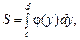 (7.21)
(7.21)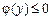 (рис. 7.14), то
(рис. 7.14), то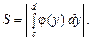 (7.22)
(7.22) ,
,  Функції
Функції 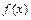 та
та 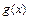 — неперервні та
— неперервні та 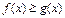 для
для  (рис. 7.15). Площа S такої фігури визначається як різниця площ фігур аА2В1b та аА2В1b
(рис. 7.15). Площа S такої фігури визначається як різниця площ фігур аА2В1b та аА2В1b (7.23)
(7.23)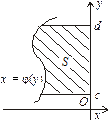

 та
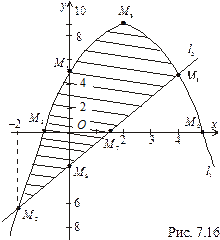
та 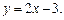
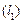 та прямою
та прямою 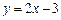
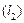 на координатній площині; при цьому знаходимо точки перетину заданих ліній між собою та з осями координат, а також координати вершини параболи (рис. 7.16).
на координатній площині; при цьому знаходимо точки перетину заданих ліній між собою та з осями координат, а також координати вершини параболи (рис. 7.16).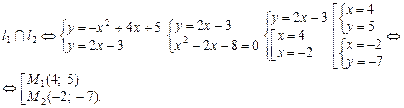
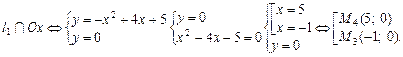

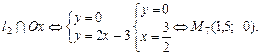

 — вершина параболи
— вершина параболи 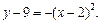
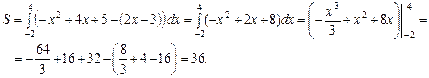
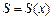 — площа поперечного перерізу тіла площиною, перпендикулярною до осі Ох у деякій точці
— площа поперечного перерізу тіла площиною, перпендикулярною до осі Ох у деякій точці 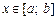 . Відрізок
. Відрізок 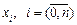 так, що
так, що 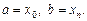 Через ці точки проведемо площини перпендикулярно до осі, у результаті чого тіло буде розбито на n частин. Кожну з цих частин наближено замінимо циліндром з висотою
Через ці точки проведемо площини перпендикулярно до осі, у результаті чого тіло буде розбито на n частин. Кожну з цих частин наближено замінимо циліндром з висотою 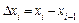 та площею основи
та площею основи  , де
, де 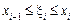 (рис. 7.17).
(рис. 7.17).
 а точне значення об’єму тіла подаватиметься границею
а точне значення об’єму тіла подаватиметься границею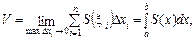 (7.24)
(7.24) утвореного обертанням навколо осі
утвореного обертанням навколо осі  фігури, обмеженої лініями
фігури, обмеженої лініями 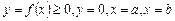 (рис. 7.18).
(рис. 7.18). в даному випадку є площа круга радіусом
в даному випадку є площа круга радіусом 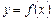 , тобто
, тобто  , а об’єм тіла обертання за формулою (7.24) буде таким:
, а об’єм тіла обертання за формулою (7.24) буде таким: (7.25)
(7.25)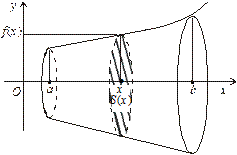
 утвореного обертанням навколо осі Оу фігури, обмеженої лініями х = 0,
утвореного обертанням навколо осі Оу фігури, обмеженої лініями х = 0,  ,
,  ,
, 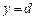 (див. рис. 7.13), матиме вигляд
(див. рис. 7.13), матиме вигляд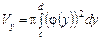 . (7.26)
. (7.26)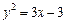 , х = 1, х = 4.
, х = 1, х = 4.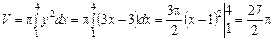 .
.