 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Б) Затухающие колебанияСтр 1 из 2Следующая ⇒
Свободные колебания в контуре
Чтобы возбудить свободные колебания в LC-контуре, сначала надо зарядить конденсатор: ключ в положении 1 соединяет его с источником напряжения. Затем переводим ключ в положение 2: пластины конденсатора замыкаются через катушку. Начинает течь ток, разряжающий конденсатор (рис. 1). Сначала ЭДС самоиндукции в катушке препятствует нарастанию тока, но когда конденсатор разрядился, ЭДС самоиндукции не позволяет току сразу исчезнуть, и он течет в прежнем направлении, перезаряжая конденсатор (рис. 2). Когда перезарядка завершена (рис. 3), ток обратного направления снова разряжает, а затем перезаряжает конденсатор. В итоге контур возвращается в начальное состояние (рис. 4). Колебания будут продолжаться сколь угодно долго, если потери энергии на активном сопротивлении катушки пренебрежимо малы. Такие колебания называют собственными. Если же потери энергии есть, колебания будут затухающими.
Получим уравнение свободных колебаний. Сумма напряжения UС на конденсаторе и
Выразим все входящие в это уравнение величины через заряд q конденсатора и его производные. Сила тока
Запишем это уравнение в виде (производные по времени обозначим точками):
где Уравнение (2) описывает свободные колебания в LC-контуре. С точно таким же уравнением мы встречались при описании механических колебаний. Сначала решим его для случая
А) Собственные колебанияописываются уравнением Его решение – гармонические колебания Сила тока в контуре меняется по закону При колебаниях происходят превращения энергии из электрической (запасенной, в основном, в электрическом поле конденсатора) в магнитную (запасенную, в основном, в магнитном поле катушки). Полная энергия
Дважды за период энергия целиком сосредоточена в электрической форме (
Б) Затухающие колебания. Решение уравнения (2) при
Частота
Демонстрации. 1. В колебательный контур низкой частоты включен гальванометр. После возбуждения колебаний в контуре стрелка гальванометра колеблется, быстро затухая. 2. Осциллограмма затухающих колебаний. Увеличивая С, уменьшаем частоту. Увеличивая R, увеличиваем затухание.
При
Для характеристики затухания, помимо коэффициента затухания · Время релаксации · Логарифмический декремент затухания равен логарифму отношения двух значений амплитуд, взятых через период колебаний: С логарифмическим декрементом связано число колебаний · Добротность контура, по определению, Можно выразить добротность через другие величины: При малом затухании (
Добротность можно связать с относительной потерей энергии за период. Энергия W, запасенная в контуре, убывает со временем как
Поиск по сайту: |


 на активном сопротивлении катушки равна действующей в контуре ЭДС самоиндукции:
на активном сопротивлении катушки равна действующей в контуре ЭДС самоиндукции: (1).
(1). ,
,  ,
,  . Подставляем в (1) и получаем:
. Подставляем в (1) и получаем: .
. , (2)
, (2)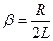 ,
,  .
. (тогда и
(тогда и  ).
).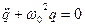 .
. с частотой
с частотой  , которая называется собственной частотой контура. Амплитуда
, которая называется собственной частотой контура. Амплитуда  и начальная фаза
и начальная фаза  определяются начальными условиями. Период собственных колебаний
определяются начальными условиями. Период собственных колебаний  (формула Томсона).
(формула Томсона). . Амплитуда силы тока
. Амплитуда силы тока  .
. .
. ) и дважды – в магнитной (
) и дважды – в магнитной (  ).
).



 - это затухающие колебания
- это затухающие колебания .
. затухающих колебаний немного меньше собственной частоты
затухающих колебаний немного меньше собственной частоты  :
: .
. Величины
Величины  и
и  Функцию
Функцию  называют амплитудой затухающих колебаний.
называют амплитудой затухающих колебаний. колебания не возникают. Критическое значение активного сопротивления, при котором исчезают колебания, находим из условия
колебания не возникают. Критическое значение активного сопротивления, при котором исчезают колебания, находим из условия  :
:  , или
, или  .
. , используют также следующие величины:
, используют также следующие величины: - это время, за которое амплитуда колебаний уменьшается в
- это время, за которое амплитуда колебаний уменьшается в  раз.
раз. .
. за время релаксации. В самом деле,
за время релаксации. В самом деле,  , а число колебаний за время
, а число колебаний за время  равно
равно  .
. .
. ,
,  .
. ) можно считать, что
) можно считать, что  ; тогда
; тогда .
.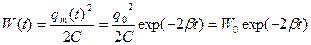 , поэтому потеря за период
, поэтому потеря за период  . Относительная потеря
. Относительная потеря  . Итак,
. Итак,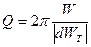 .
.