 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Распространение света внутри анизотропных средСтр 1 из 2Следующая ⇒
Оптической анизотропией называется зависимость оптических свойств среды от направления, которая объясняется тем, что в разных направлениях электрические и магнитные характеристики среды отличаются друг от друга. Будем считать среду немагнитной, поскольку к таким относится большинство оптических материалов, т.е. будем учитывать лишь диэлектрическую анизотропию, (исключение составляют лишь прозрачные ферриты). Электромагнитные свойства диэлектрических сред описываются лишь ε и μ – диэлектрической и магнитной проницаемостью и фигурируют в двух уравнениях Максвелла, называемых материальными. В случае изотропной среды они выглядят следующим образом
где Появление анизотропии означает, что в немагнитных средах
где
Уравнение (2) теперь можно переписать в компонентах
где для удобства заменена индексация Рассмотрим распространение плоских волн в таких средах. Из предыдущего известно, что для векторов
где Подставляя эти выражения в уравнения Максвелла и учитывая, что
из вторых
Исключая из уравнений (6а) и (6б )напряженность
Воспользовавшись (8) , выражением для
Если выбрать систему координат так, что направление распространения волны будет совпадать с осью
Решение получившейся системы относительно 1) решение будем нетривиальным ( 2) каждому собственному значение будет соответствовать собственный вектор, которые к тому же будут перпендикулярны, что следует из симметрии тензора Равенство нулю детерминанта сводится к квадратному уравнению относительно
Откуда следует, что в общем случае в анизотропной среде в заданном направлении могут распространяться две волны с разными скоростями
а направления поляризации этих волн взаимно перпендикулярны. Известно, что соответствующим выбором осей координат, тензор можно привести к диагональному виду
Уравнение (4) можно переписать как
Так как Из тензорной алгебры известно, что каждому тензору соответствует так называемый характеристический эллипсоид, выражение для которого будет выглядеть следующим образом
Это уравнение поверхности эллипсоида, который поворотом системы координат может быть приведен к каноническому виду (в выражении (15) тогда будут отсутствовать перекрестные члены, т.е. выражение в скобках будет равно нулю). В этой же новой системе координат тензор диэлектрической проницаемости примет т.н. диагональную форму - все недиагональные элементы тензора будут равны нулю:
Оси такой системы координат называются главными осями тензора - в данном случае главными осями тензора диэлектрической проницаемости. При таком выборе системы координат соотношение (15) записываются особенно просто и, что очень важно, можно определить три показателя преломления соотношениями (17)
и с помощью их образовать эллипсоид
который называется оптическая индикатриса. Очевидно, что главные оси так определенного эллипсоида совпадают с главными осями тензора диэлектрической проницаемости и называются главными осями оптической индикатрисы. Оптическая индикатриса и соответствующие им среды могут быть трех типов: 1. 2. 3. Распространение световой волны вдоль оси симметрии не отличается от распространения в изотропной среде. Такое особое направление называется главной осью среды, а среда (или кристалл) называется соответственно одноосной (случай 2) или двухосной (случай 3). Параметры световой волны, распространяющейся в такой среде, зависят от ее ориентации - направления распространения и направления поляризации относительно главных осей среды и могут быть определены с помощью оптической индикатрисы. Зная величины полуосей оптической индикатрисы, ее форму и ориентацию в среде, можно определить скорости, показатели преломления и плоскости колебаний (поляризации) для волн, распространяющихся в среде в любом направлении. На рис. 2 изображен вырезанный из одноосного, для простоты, кристалла образец, имеющий прямоугольную форму. Главная ось в нем занимает произвольное направления и в рассматриваемом случае совпадает с
где
Если построить центральное сечение эллипсоида оптической индикатрисы перпендикулярно Заметим, что если длины полуосей эллипса одинаковы, то при любом направлении распространения
Явление двойного лучепреломления, было экспериментально обнаружено при освещении кристалла
Поиск по сайту: |
 ,
,
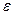 и
и 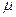 скаляры. Так как оптические материалы немагнитны, то
скаляры. Так как оптические материалы немагнитны, то 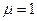 , а
, а 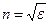 - показатель преломления. В этом случае
- показатель преломления. В этом случае 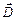 ||
||  и
и 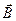 ||
||  .
. не параллельна
не параллельна  и
и 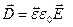 ,
,
 - так называемый тензор. Этот объект является оператором, ставящий в соответствие одному вектору другой и имеет вид матрицы
- так называемый тензор. Этот объект является оператором, ставящий в соответствие одному вектору другой и имеет вид матрицы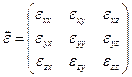 .
.
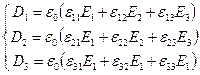 ,
,
 , и тогда тензор
, и тогда тензор  .Тензор
.Тензор  . Это очень важное свойство, оно используется в кристаллофизике.
. Это очень важное свойство, оно используется в кристаллофизике. - напряженностей электрического и магнитных полей и
- напряженностей электрического и магнитных полей и 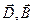 -соответствующих им индукций, выражения для плоских волн имеют вид
-соответствующих им индукций, выражения для плоских волн имеют вид (а);
(а);  (б);
(б);
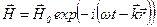 (в);
(в);  (г),
(г),
 - вектор текущих координат,
- вектор текущих координат,  - волновой вектор, v – фазовая скорость,
- волновой вектор, v – фазовая скорость, 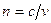 - показатель преломления, с – скорость света в вакууме.
- показатель преломления, с – скорость света в вакууме. , т.е.
, т.е.  , получим из первых двух уравнений
, получим из первых двух уравнений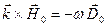 (а);
(а); 
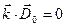 (а);
(а); 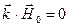 .
.
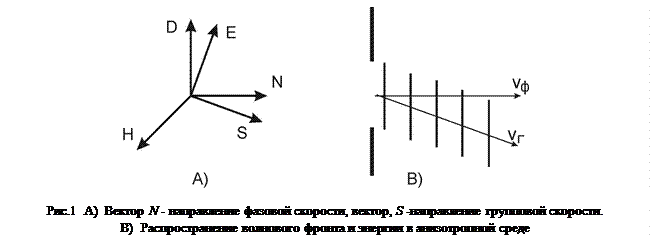
 Из уравнений (7) следует, что вектор направления распространения волновой поверхности
Из уравнений (7) следует, что вектор направления распространения волновой поверхности 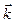 и, соответственно, вектор фазовой скорости
и, соответственно, вектор фазовой скорости 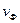 перпендикулярны векторам напряженности магнитного поля
перпендикулярны векторам напряженности магнитного поля  и вектору электрической индукции
и вектору электрической индукции 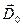 .Направление же распространения энергии определяется вектором Пойнтинга
.Направление же распространения энергии определяется вектором Пойнтинга 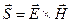 , которое совпадает с направлением групповой скорости
, которое совпадает с направлением групповой скорости  и перпендикулярно, соответственно, векторам
и перпендикулярно, соответственно, векторам  и
и 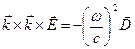 .
.
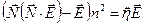 .
.
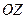 , т.е.
, т.е. 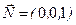 , то выражение (9) значительно упростится, и в координатах будет выглядеть следующим образом
, то выражение (9) значительно упростится, и в координатах будет выглядеть следующим образом .
.
 ) если детерминант этой системы не равен нулю – т.е.
) если детерминант этой системы не равен нулю – т.е. 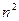 является собственным значением;
является собственным значением; (на этот счет имеются соответственные теоремы).
(на этот счет имеются соответственные теоремы).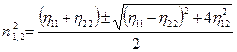 ,
,
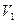 ,
, 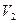 , соответствующим двум показателям преломления – решения уравнения (10)
, соответствующим двум показателям преломления – решения уравнения (10)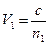 ;
; 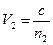 ,
,
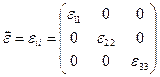 ,
,
 .
.
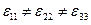 , то
, то 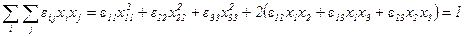 .
.
 .
.
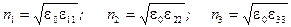
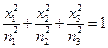 ,
,
 - Оптическая индикатриса - сфера, среда изотропная, любое направление является осью симметрии.
- Оптическая индикатриса - сфера, среда изотропная, любое направление является осью симметрии.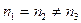 - Оптическая индикатриса - эллипсоид вращения, среда анизотропная, имеется лишь одна ось симметрии.
- Оптическая индикатриса - эллипсоид вращения, среда анизотропная, имеется лишь одна ось симметрии.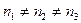 - Оптическая индикатриса - эллипс общего вида, среда анизотропная, из теории поверхностей второго порядка известно, что у такого эллипсоида имеется две оси симметрии, т.е. можно показать, что у такого эллипсоида два круговых сечения.
- Оптическая индикатриса - эллипс общего вида, среда анизотропная, из теории поверхностей второго порядка известно, что у такого эллипсоида имеется две оси симметрии, т.е. можно показать, что у такого эллипсоида два круговых сечения. . В соответствии с этим направлением поострена оптическая индикатриса - эллипс с полуосями
. В соответствии с этим направлением поострена оптическая индикатриса - эллипс с полуосями 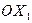 ,
, 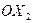 и
и 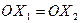 , т.е. уравнение эллипса в системе координат с осями
, т.е. уравнение эллипса в системе координат с осями  , называемой кристаллофизической системой координат.
, называемой кристаллофизической системой координат. ,
,
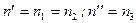 в соответствии с (9).
в соответствии с (9).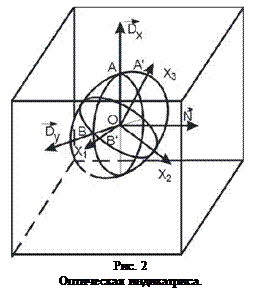 Направление световой волны совпадает с направлением
Направление световой волны совпадает с направлением 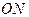 , т.е. с нормалью к волновому фронту. Следует отметить, что в анизотропных средах направление световой волны не совпадает с направлением распространения энергии и эти направления необходимо различать. В изотропных средах это различие отсутствует.
, т.е. с нормалью к волновому фронту. Следует отметить, что в анизотропных средах направление световой волны не совпадает с направлением распространения энергии и эти направления необходимо различать. В изотропных средах это различие отсутствует. и
и 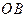 будут определять соответственно направления колебаний векторов колебаний
будут определять соответственно направления колебаний векторов колебаний 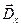 и
и 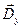 этих волн. Длины полуосей равны показателям преломления для волн, у которых колебания происходят в плоскостях, содержащих
этих волн. Длины полуосей равны показателям преломления для волн, у которых колебания происходят в плоскостях, содержащих  и
и 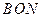 . Таким образом, как уже говорилось, плоская электромагнитная волна с произвольным направлением вектора
. Таким образом, как уже говорилось, плоская электромагнитная волна с произвольным направлением вектора  называется главной осью кристалла, и сечение перпендикулярное ей является окружностью, т.е. показатели преломлений для направлений
называется главной осью кристалла, и сечение перпендикулярное ей является окружностью, т.е. показатели преломлений для направлений  и перпендикулярным ему
и перпендикулярным ему 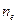 будет максимальной. Разность
будет максимальной. Разность 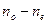 называется двойным лучепреломлением, а показатели преломлений
называется двойным лучепреломлением, а показатели преломлений  , среда изотропна и луч в ней будет только обыкновенным.
, среда изотропна и луч в ней будет только обыкновенным.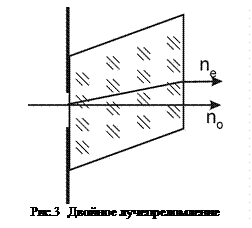 Анизотропия кристаллов обусловлена строением его решетки. Атомы и молекулы, из которых он построен, расположены в определенном порядке, но этот порядок неодинаков для всех направлений. Например, расстояние между атомами, строго одинаковые вдоль какой-то оси, могут быть другими вдоль других осей.
Анизотропия кристаллов обусловлена строением его решетки. Атомы и молекулы, из которых он построен, расположены в определенном порядке, но этот порядок неодинаков для всех направлений. Например, расстояние между атомами, строго одинаковые вдоль какой-то оси, могут быть другими вдоль других осей. (исландский шпат) при освещении его узким пучком света. Опыт показал, что в этом случае в нем возникли два луча – обыкновенный и необыкновенный. Для необыкновенного луча показатель преломления
(исландский шпат) при освещении его узким пучком света. Опыт показал, что в этом случае в нем возникли два луча – обыкновенный и необыкновенный. Для необыкновенного луча показатель преломления 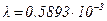 мм, то
мм, то 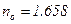 , а
, а 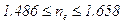 . Следовательно
. Следовательно  - такие кристаллы называются отрицательными, если
- такие кристаллы называются отрицательными, если 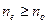 - то положительными.
- то положительными.