 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Гідродинаміка потоку в трубі ⇐ ПредыдущаяСтр 8 из 8
Рух крові по судинах з деяким наближенням можна розглядати як рух рідини з певними реологічними властивостями по трубі круглого перерізу. Обмежимося розглядом ламінарного стаціонарного потоку, хоча на деяких ділянках артеріальної системи течія не є ні стаціонарною, ні ламінарною, а пульсуючою. В капілярній системі кровообігу такий підхід взагалі є неприйнятний, оскільки розміри кров'яних клітин є співмірні з діаметром судин. Рушійна сила течії Fm у достатньо довгому циліндрі радіуса r дорівнює де DР - перепад тисків. У стаціонарному потоці ця сила компенсується силою тертя Fmp, яка пропорційна площі бокової поверхні циліндра S6 і градієнту швидкості v'
де
Тоді
У стаціонарному випадку Fm = Fmp. Якщо припустити, що біля поверхні стінок існує безмежно тонкий нерухомий шар рідини, тобто при r=R, v(R)=0і координата у змінюється усередину труби по радіусу, тобто r=R-y, dr=-dy (рис. 10.1), отримаємо
Після заміни змінних та інтегрування останнього співвідношення отримаємо розподіл швидкості рідини по перерізу труби
Отже, швидкість у трубі розподіляється за параболічним законом (рис. 10.1), причому на осі труби r=0вона набуває максимального значення vmax
або, підставляючи (10.2) в (10.1), отримуємо
Середня за площею поперечного перерізу швидкість vсрзнаходиться інтегруванням (10.3) в полярних координатах:
З урахуванням (10.3) маємо
Формула Хагана-Пуазейля зв'язує розхід рідини (об’ємну швидкість) з перепадом тиску. Отримати її можна як добуток середньої швидкості течії на площу перерізу
Об'ємна швидкість рідини При протіканні рідини через труби змінного перерізу існує взаємозв'язок між радіусом, швидкістю і тиском (рис. 10.2).
де А - площа перерізу труби. Крім цього, із закону збереження енергії витікає рівняння Бернуллі (при нехтуванні в'язкістю)
де р0 - гідростатичний тиск у точці при v = 0. Для кровоносних судин врахування внутрішнього тиску і його зміни має велике значення, оскільки він призводить до пружної або в'язкопружної деформації стінок e
Нехай на ділянці l під дією тиску рідини Р виникають пружні деформації e, тоді за законом Гука напруження s в стінці труби дорівнюють
де Е – модуль Юнга стінок труби. Напруження також можна визначити як відношення сили, яка розтягує трубу в радіальному напрямку, до площі поперечного перерізу стінки труби s=l·d, товщина якої дорівнює d
Пронормуємо силу за довжиною труби
тоді
Сила розтягання F1стінки труби спричиняється тиском Р і залежить від радіуса труби. Визначається вона з рівняння Лапласа
У стаціонарному режимі напруження, спричинені тиском рідини, компенсуються пружними напруженнями
де Ed – жорсткість стінки труби. Отже, радіальна деформація труби
– пропорційна до внутрішнього тиску і квадрата радіуса труби, але обернено пропорційна до жорсткості стінки труби. Відносна радіальна деформація, яка визначається напруженням, – пропорційна радіусу труби
З (10.6) випливає важливий для вивчення кровоносної системи висновок, що при одному і тому ж тискові судини більшого діаметра піддаються більшим деформуючим напруженням у порівнянні з дрібними судинами. Рух крові в судинах Гемодинаміка – галузь науки, яка вивчає фізичні особливості протікання крові в судинах. Суттєвий вклад у розвиток гемодинаміки зробив лікар і фізіолог Жан Луі Марі Пуазейль (1799-1869). Сучасна гемодинаміка у зв'язку із швидким розвитком медичної техніки розв'язує задачі, які виникають при конструюванні пристроїв екстракорпорального кровообігу (штучна нирка, апарат "серце-легені", протези судин та клапанів серця тощо). Гемодинамічні дослідження мають велике значення для діагностики і терапії серцево-судинних захворювань. Основні особливості течії в кровоносній системі: 1) протікання крові в артеріальній системі має пульсуючий характер; 2) судини розтягуються у повздовжньому і радіальному напрямах, вони є непрямолінійними і розгалуженими; 3) протікання крові в крупних судинах має турбулентний характер зі значними вхідними ефектами; 4) в капілярах кров не можна розглядати як однорідну рідину; 5) кров веде себе як псевдопластична тиксотропна рідина, на в'язкість якої також впливає ефект Фареуса-Ліндквіста. Ці обставини утруднюють гідродинамічні розрахунки протікання крові, тому експериментальні дослідження набирають особливої ваги (прозорі трубки, ультразвукова діагностика, лазерна доплерівська анемометрія тощо). Деякі експериментально отримані гідродинамічні характеристики системи кровообігу людини зведені в табл. 10.1. Відомі геометричні і гідродинамічні характеристики системи кровообігу дозволяють зіставляти їх, а також здійснювати моделювання процесів, які відбуваються у системі кровообігу, що сприяє глибшому розумінню функціонального призначення окремих елементів, відділів і системи в цілому. Таблиця 10.1. Деякі експериментально отримані гідродинамічні характеристики системи кровообігу людини
Кров'яний тиск
Максимальний тиск, який досягається у момент викиду крові із серця в аорту, називається систолічним.Після повного виштовхування крові з серця і закриття аортальних клапанів тиск падає до значення, яке відповідає діастолічномутиску. Різниця між систолічним і діастолічним тисками називається пульсовим тиском(рис. 10.4). Коливання кров'яного тиску зумовлені пульсуючим характером кровотоку і високою еластичністю та розтягувальною здатністю судин. У людини при віддаленні від аорти змінюється форма і амплітуда пульсової хвилі.
Поиск по сайту: |
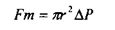
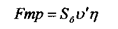
 , l- довжина труби,
, l- довжина труби,
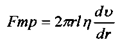

 (10.1)
(10.1)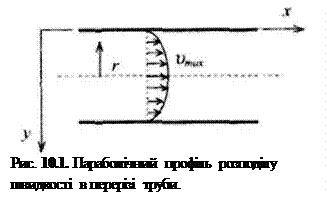
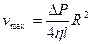 (10.2)
(10.2)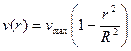 (10.3)
(10.3) . (10.2)
. (10.2) .
.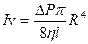 (10.4)
(10.4) в трубі вимірюється в м3/с і є пропорційна четвертому степеню радіуса труби. При збільшенні радіуса труби в 1,2 рази об'ємний розхід рідини збільшиться більш ніж вдвічі при незмінному перепаді тиску.
в трубі вимірюється в м3/с і є пропорційна четвертому степеню радіуса труби. При збільшенні радіуса труби в 1,2 рази об'ємний розхід рідини збільшиться більш ніж вдвічі при незмінному перепаді тиску. Причому для ньютонівських рідин виконується співвідношення
Причому для ньютонівських рідин виконується співвідношення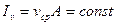 ,
,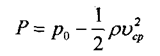
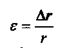
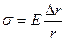

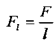
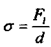
 (10.5)
(10.5)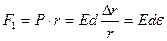
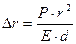 (10.6)
(10.6)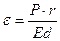 (10.6а)
(10.6а)
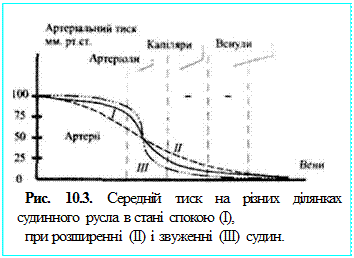 Рушійною силою, яка змушує кров переміщатись по судинах в напрямку аорта ® артерії ® капіляри ® венули ® крупні вени ® порожнисті вени є відповідний градієнт кров'яного тиску. Усереднені значення артеріального і венозного кров'яного тиску для різного ступеня розширеності судин показані на рис. 10.3.
Рушійною силою, яка змушує кров переміщатись по судинах в напрямку аорта ® артерії ® капіляри ® венули ® крупні вени ® порожнисті вени є відповідний градієнт кров'яного тиску. Усереднені значення артеріального і венозного кров'яного тиску для різного ступеня розширеності судин показані на рис. 10.3.