 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Правила дифференцирования. 1. Производная суммы двух функций равна сумме производных этих функций
1. Производная суммы двух функций равна сумме производных этих функций, то есть
Доказательство. Пусть
2. Производная произведения: Доказательство. Пусть
откуда следует
При получении этой формулы используются два свойства пределов: предел произведения равен произведению пределов, и предел функции
3. Производная частного двух функций:
Формула приводится без доказательства (с ним можно познакомиться в одном из рекомендованных учебников). 4. Производная сложной функции. Пусть
здесь Доказательство.
При доказательстве формулы использовался переход от вычисления предела при Следствие. Это свойство можно обобщить и на большее количество промежуточных аргументов функции. Рассмотрим, например, функцию
5. Производная обратной функции. Рассмотрим функцию
В доказательстве формулы использовался переход от вычисления предела при
Для дальнейшей работы с производными необходима таблица производных элементарных функций.
Таблица производных
1. Доказательство. Поскольку 2. Докажем это свойство для
Для других 3. Доказательство:
При вычислении второго из пределов сделана замена переменной 4. 5. Доказательство:
6. 7. Доказательство:
8. 9. Доказательство:
10. 11. Доказательство. Пусть
откуда следует
В ходе доказательства использовались следующие свойства логарифмов: а) также использовалась замена переменной
12. Формула является следствием предыдущей формулы.
13. Пусть
14. Для вычисления производных большинства функций достаточно знать таблицу производных элементарных функций и уметь применять правила дифференцирования. Иногда удобно готовить функцию к дифференцированию, приводя ее к наиболее удобному для вычисления производной виду.
Примеры вычисления производных 1.
При вычислении производной использовались правила производной от суммы и произведения, таблица производной. Второе слагаемое функции 2. 3. В вышеприведенных примерах дифференцируемые функции являлись либо комбинациями простых функций, либо приводились к таким комбинациям. При вычислении производных сложных функций существенно используется правило дифференцирования сложных функций с фактическим или мысленным введением одного и более промежуточных аргументов. 4.
5.
Из последних двух примеров следует, что при вычислении производных сложных функций вначале вводится необходимое количество промежуточных аргументов, после чего функции становятся простыми, это позволяет произвести дифференцирование, затем для получения ответа необходимо избавиться от этих промежуточных аргументов. Это обстоятельство приводит к идее о "мысленном" введении этих промежуточных аргументов, тогда нет необходимости избавляться от них в конце решения. В этом случае вводится следующее правило вычисления производных: производная функции представляет собой произведение производной по сложному аргументу на производную от этого сложного аргумента. При этом обычно действуют в направлении, противоположном вычислению функции. Рассмотрим вначале те же примеры. 4'. Функция
При этом мысленно вводится аргумент 5'.
Мысленное введение промежуточных аргументов в процессе дифференцирования делает функции, как бы, простыми, что позволяет использовать таблицу производных. 6.
7.
Примеры для самостоятельного решения
Вычислить 7.1
7.4.
7.7
В этой главе примеры для самостоятельной работы приводятся без ответов, ибо ответ в данном случае является решением задачи.
Поиск по сайту: |
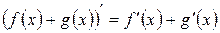 .
. , тогда
, тогда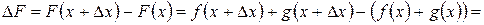


 .
. , тогда
, тогда
 ,
,
 .
. , не зависящей от
, не зависящей от  , равен самой функции.
, равен самой функции. .
. , где
, где  , тогда
, тогда ,
, есть искомая производная функции
есть искомая производная функции  по переменной
по переменной  , а
, а  производная этой же функции по промежуточному аргументу
производная этой же функции по промежуточному аргументу 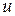 .
. .
. к пределу при
к пределу при  . Этот переход законен, если
. Этот переход законен, если  непрерывная функция, что следует из третьего определения непрерывности функции.
непрерывная функция, что следует из третьего определения непрерывности функции. , где
, где  . Очевидно, промежуточных аргументов здесь два
. Очевидно, промежуточных аргументов здесь два 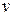 , тогда
, тогда  и так далее.
и так далее. и обратную ей
и обратную ей  . Установим связь между производными этих функций.
. Установим связь между производными этих функций. .
. , если
, если  постоянная.
постоянная. . Очевидно,
. Очевидно,  .
. для любых
для любых  .
. . Пусть
. Пусть  , тогда
, тогда ,
, .
. .
. ,
,

 .
.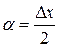 , затем использован первый замечательный предел.
, затем использован первый замечательный предел. (доказывается аналогично).
(доказывается аналогично). .
.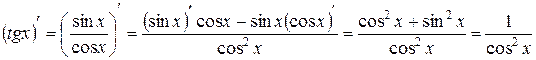 .
. . Доказательство аналогично.
. Доказательство аналогично. .
.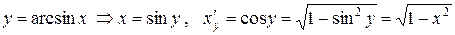 , откуда имеем
, откуда имеем .
. . Доказывается аналогично.
. Доказывается аналогично. .
.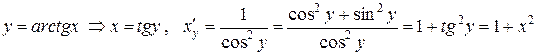 ,
, .
.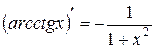 .
.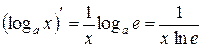 .
. , тогда
, тогда
 ,
,
 .
. , б)
, б)  , в)
, в)  ,
, , после чего – второй замечательный предел. Постоянная
, после чего – второй замечательный предел. Постоянная  и натуральный логарифм
и натуральный логарифм  были введены при рассмотрении второго и третьего замечательных пределов. Поскольку логарифм – функция непрерывная, перестановка местами логарифма и предела следует из первого определения непрерывности функции:
были введены при рассмотрении второго и третьего замечательных пределов. Поскольку логарифм – функция непрерывная, перестановка местами логарифма и предела следует из первого определения непрерывности функции:  .
. .
. .
. тогда
тогда  , следовательно,
, следовательно, .
. . Формула является следствием предыдущей.
. Формула является следствием предыдущей. ,
, .
.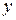 преобразовано к более удобному для дифференцирования виду.
преобразовано к более удобному для дифференцирования виду. .
. .
.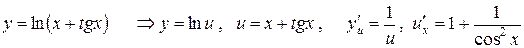 ,
,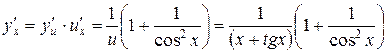 .
. ,
, ,
, .
. вычисляется следующим образом. Вначале вычисляется выражение
вычисляется следующим образом. Вначале вычисляется выражение 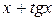 , затем логарифм этого выражения. Дифференцируем в противоположном направлении. Производная от логарифма умножается на производную от выражения под знаком логарифма.
, затем логарифм этого выражения. Дифференцируем в противоположном направлении. Производная от логарифма умножается на производную от выражения под знаком логарифма. .
. . Следует отметить, что результат в последнем случае получается гораздо быстрее, чем в первом.
. Следует отметить, что результат в последнем случае получается гораздо быстрее, чем в первом.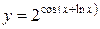 . При вычислении функции определяем вначале выражение
. При вычислении функции определяем вначале выражение  , затем косинус этого выражения, после чего получаем значение показательной функции. Вычисляем производную в обратном порядке: вначале производная от показательной функции, умножаем ее на производную от косинуса, и, наконец, на производную от суммы функций. Тогда
, затем косинус этого выражения, после чего получаем значение показательной функции. Вычисляем производную в обратном порядке: вначале производная от показательной функции, умножаем ее на производную от косинуса, и, наконец, на производную от суммы функций. Тогда .
. ,
, ,
, .
.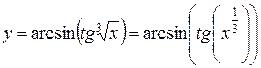 ,
, .
.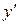
 , 7.2
, 7.2 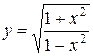 , 7.3
, 7.3  ,
, , 7.5
, 7.5  , 7.6
, 7.6  ,
, , 7.8
, 7.8  , 7.9
, 7.9  .
.