 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Процесс ортогонализации Шмидта ⇐ ПредыдущаяСтр 2 из 2
Теорема 6.4. В любом конечномерном евклидовом пространстве существует ортонормированный базис. ►Выберем в
и на его основе построим систему векторов:
При любом Подберем коэффициенты
откуда следует, что
После конечного числа шагов получаем ортогональную систему ненулевых векторов Процесс доказательства теоремы 6.4 и называется процессом ортогонализации Шмидта. Пример. В пространстве многочленов степени не выше двух, в котором скалярное произведение задается формулой
построим ортонормированный базис, исходя из базиса
▼Поступаем точно так же, как и при доказательстве теоремы. Положим
Таким образом, получили ортогональный базис
Теперь эти векторы остается пронормировать.
Итак, ортонормированный базис:
§ 6. Выражение скалярного произведения через координаты перемножаемых векторов Определение.Матрицей Грама системы векторов
евклидова пространства Нетрудно показать, что в случае действительного пространства матрица Г симметричная и все ее главные миноры положительны. Если же пространство комплексное, то
Определение. Комплексная квадратная матрица Г, удовлетворяющая условию (6.10) называется эрмитовой. Таким образом, матрица Грама любой системы векторов комплексного евклидова пространства является эрмитовой. Кроме того, можно также показать, что все ее главные миноры положительны. В частности, матрицу Грама можно определить и для произвольного базиса. Очевидно, для ортонормированности базиса необходимо и достаточно, чтобы его матрица Грама была единичной. Выберем в
и обозначим
координатная форма записи скалярного произведения в комплексном евклидовом пространстве;
координатная форма записи скалярного произведения в действительном пространстве. Так как
матричная форма записи скалярного произведения в комплексном пространстве;
в действительном пространстве. В ортонормированном базисе скалярное произведение вычисляется так:
координатная форма записи скалярного произведения в комплексном евклидовом пространстве;
в действительном пространстве;
матричная форма записи скалярного произведения в комплексном пространстве;
в действительном пространстве.
Поиск по сайту: |
 какой-либо базис
какой-либо базис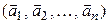 (6.7)
(6.7)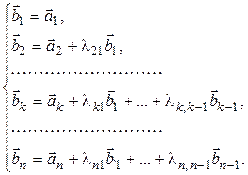 (6.8)
(6.8) и при любом наборе
и при любом наборе  вектор
вектор  , так как он представляет собой линейную комбинацию линейно независимых векторов
, так как он представляет собой линейную комбинацию линейно независимых векторов  , причем коэффициент при
, причем коэффициент при  отличен от нуля (равен 1).
отличен от нуля (равен 1). был ортогонален всем предыдущим. Для этого
был ортогонален всем предыдущим. Для этого 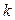 -е равенство из (6.8) умножим скалярно справа на
-е равенство из (6.8) умножим скалярно справа на  . Например, при
. Например, при  ,
, . При остальных умножениях уже учтем, что
. При остальных умножениях уже учтем, что  при
при  .
.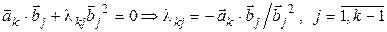 .
. 
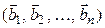 , которая по теореме 6.3 линейно независима, а значит, в
, которая по теореме 6.3 линейно независима, а значит, в  -мерном евклидовом пространстве является базисом. Для того чтобы получить ортонормированный базис, векторы
-мерном евклидовом пространстве является базисом. Для того чтобы получить ортонормированный базис, векторы  осталось только пронормировать, т. е. каждый разделить на его длину.◄
осталось только пронормировать, т. е. каждый разделить на его длину.◄ ,
, .
. и подберем числа
и подберем числа 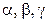 так, чтобы функции
так, чтобы функции  были ортогональными.
были ортогональными.

 .
. .
. .
. .▲
.▲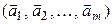 (6.9)
(6.9) , где
, где  .
.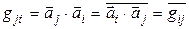 , т. е.
, т. е. . (6.10)
. (6.10) (6.11)
(6.11) пространства
пространства  –
– –
– , то
, то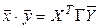 –
– –
– –
– –
–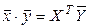 – (6.12)
– (6.12)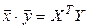 –
–