 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Псевдоевклидово пространствоСтр 1 из 2Следующая ⇒
ГЛАВА 6. ЕВКЛИДОВЫ ПРОСТРАНСТВА Действительные евклидовы пространства
Определение. Говорят, что на действительном линейном пространстве 1*. 2*. 3*. 4*. Простейшие следствия из аксиом
1º. ► 2º. ► 3º. ► Итак, скалярное произведение на действительном линейном пространстве – это функция двух векторных аргументов. На основании второй и третьей аксиом она линейна по первому аргументу, а на основании следствий из аксиом – линейна и по второму, т. е. это билинейная форма. Из первой аксиомы вытекает, что эта билинейная форма симметрична, а из четвертой – что она еще и положительно определена. Таким образом, скалярное произведение на действительном линейном пространстве – это положительно определенная симметричная билинейная форма. Определение. Действительным евклидовым (или просто евклидовым) пространством называется действительное линейное пространство, в котором задана операция скалярного произведения. Примеры действительных евклидовых пространств
1. Пространство 2. Пространство
(см.§ 5гл.3). 3. Пространство
Очевидно, трем первым аксиомам скалярного произведения оно удовлетворяет. Проверка четвертой аксиомы – несложное упражнение из математического анализа. Евклидово пространство будем обозначать буквой
Псевдоевклидово пространство
Иногда в определении скалярного произведения на действительном линейном пространстве отказываются от положительной определённости билинейной формы, заменяя её невырожденностью, т. е. называют скалярным произведением симметричную невырожденную билинейную форму. Действительное линейное пространство с введенным таким образом скалярным произведением называется псевдоевклидовым.
Поиск по сайту: |
 задана операция скалярного произведения, если задан закон, по которому каждой паре элементов
задана операция скалярного произведения, если задан закон, по которому каждой паре элементов  ставится в соответствие действительное число, которое называется их скалярным произведением, обозначается
ставится в соответствие действительное число, которое называется их скалярным произведением, обозначается 
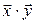 и удовлетворяет следующим аксиомам:
и удовлетворяет следующим аксиомам: .
. .
.
 причем
причем  .
.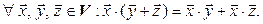
 [1*] =
[1*] =  [2*] =
[2*] =  = [1*] =
= [1*] =  ◄
◄
 = [1*] =
= [1*] =  = [3*] =
= [3*] =  = [1*] =
= [1*] =  ◄
◄
 ◄
◄ свободных векторов с введенным в нем обычным скалярным произведением
свободных векторов с введенным в нем обычным скалярным произведением  . Очевидно, всем аксиомам скалярного произведения оно удовлетворяет (эти аксиомы просто «списаны» со свойств обычного скалярного произведения).
. Очевидно, всем аксиомам скалярного произведения оно удовлетворяет (эти аксиомы просто «списаны» со свойств обычного скалярного произведения). , в котором скалярное произведение задается равенством
, в котором скалярное произведение задается равенством
 непрерывных на отрезке
непрерывных на отрезке  функций, в котором скалярное произведение задается так:
функций, в котором скалярное произведение задается так: .
. . Если соответствующее ему линейное пространство n-мерно, то и евклидово называется n-мерным и обозначается
. Если соответствующее ему линейное пространство n-мерно, то и евклидово называется n-мерным и обозначается  .
.