 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Дифференциальные формы функции ⇐ ПредыдущаяСтр 5 из 5
Любую функцию f от n переменных можно рассматривать как функцию f: Rп®R, ставящую в соответствие произвольной точке X=(x1, x2, …, xn) из Rп некоторое число. Поэтому любую функцию f от n переменных можно рассматривать как функцию f(X) на некотором множестве MÍRп, и все понятия, связанные с понятием функции многих переменных, переносятся на функции на Rп (в частности, такие понятия, как непрерывность, дифференцируемость и другие). Тем не менее, мы напомним некоторые понятия и факты, а также введём некоторые другие. Поверхностью уровня функции f(X) называется множество точек, в которых функция принимает постоянное значение: f(X)=const. Если n=2, поверхность уровня носит название линии уровня. Градиентом Ñf(X0) непрерывно дифференцируемой функции f(X) в точке X0ÎRп называется вектор-столбец, элементами которого являются частные производные первого порядка, вычисленные в данной точке: Ñf(X0)= Градиент функции направлен по нормали к поверхности уровня, то есть перпендикулярно к касательной плоскости, проведённой в точке X0, в сторону наибольшего возрастания функции. Так как градиент функции является вектором, то для градиентов нескольких функций можно рассматривать их линейную зависимость. Матрицей ГессеH(X) в точке X дважды непрерывно дифференцируемой функции f(X) называется матрица частных производных второго порядка, вычисленных в данной точке: H(X)= = где hij= Первым дифференциалом функцииf(X) (по переменным x1, x2, …, xn) называется функция df(X)= Вторым дифференциалом функцииf(X) (по переменным x1, x2, …, xn) называется функция d2f(X)= Введём обозначение: DX=(Dx1, Dx2, …, Dxn). Тогда DX×H(X)×DXТ=(Dx1, Dx2, …, Dxn) является квадратичной формой от переменных Dx1, Dx2, …, Dxn. С помощью критериев 2.2 и 2.3 можно исследовать знакоопределённость матрицы Гессе. Экстремумы функции Точка X0 называется точкой локального минимума (максимума) функции f(X), если существует e-окрестность Oe(X0) точки X0, такая, что при всех XÎOe(X0) выполняется неравенство f(X0)£f(X) (f(X0)³f(X)). Точки локального минимума и максимума называются точками экстремума этой функции. Если в этом определении убрать условие, связанное с e-окрестностью, то получим определение глобального минимума (максимума) функции. Из определения вытекает, что точки экстремума функции всегда являются внутренними точками области определения функции. Ясно, что еслиX0 является точкой максимума функции f(X), то она является точкой минимума для функции -f(X). Поэтому в дальнейшем можно рассматривать, например, точки минимума. Точка X0 называется стационарной точкой функции f(X), если в этой точке градиент функции f(X) является нулевым вектором, то есть Выпуклость Пусть функция y=f(X) определена на выпуклом множестве MÍRп. Она называется выпуклой (вогнутой) на M, если для любых точек A=(a1, a2, …, an), B=(b1, b2, …, bn), принадлежащих M, и для любого действительного числа 0£a£1 выполняется неравенство f(C)£af(A)+(1-a)f(B), (f(C)³af(A)+(1-a)f(B)) где C=(aa1+(1-a)b1, aa2+(1-a)b2, …, aan+(1-a)bn). Переходя в определении выпуклой (вогнутой) функции к строгим неравенствами, мы получаем определения соответственно строго выпуклой (строго вогнутой) функции. В случае, когда y=f(x) - функция одной переменной, геометрический смысл выпуклости функции заключается в том, что на множестве MÍR график функции располагается не выше (любой) секущей, проведённой через произвольные две точки (a, f(a)) и (b, f(b)) графика функции, где [a, b]ÍM, а геометрический смысл вогнутости функции заключается в том, что на множестве MÍR график функции располагается не ниже (любой) секущей, проведённой через произвольные две точки (a, f(a)) и (b, f(b)) графика функции, где [a, b]ÍM (рис. ). Таким образом, выпуклость функции соответствует выпуклости функции вниз, а вогнутость - выпуклости вверх. Аналогично, когда z=f(x, y) - функция двух переменных, то геометрический смысл выпуклости функции заключается в том, что на множестве MÍR2 график функции (некоторая поверхность) располагается не выше (любой) секущей, проведённой через произвольные две точки (a1, a2, f(a1, a2)) и (b1, b2, f(b1, b2)) графика функции, где {A=(a1, a2), B=(b1, b2)}ÍM, а геометрический смысл вогнутости функции заключается в том, что на множестве MÍR график функции располагается не ниже (любой) секущей, проведённой через произвольные две точки (a1, a2, f(a1, a2)) и (b1, b2, f(b1, b2)) графика функции. Ясно, что если функция f(X) является (строго) выпуклой (вогнутой), то функция -f(X) является (строго) вогнутой (выпуклой). Поэтому в дальнейшем можно из этих классов функций рассматривать, например, выпуклые функции. Выпуклые функции обладают следующими свойствами: 1о. Если f(X) - выпуклая функция на выпуклом множестве M, то всякая точка локального минимума является точкой её глобального минимума на M. 2о. Если выпуклая функция достигает своего минимума в двух различных точках, то она достигает минимума во всех точках отрезка, соединяющего эти две точки. 3о. Если f(X) - строго выпуклая функция на выпуклом множестве M, то она может достигать своего глобального минимума на M не более чем в одной точке. Выпуклость функции можно определить по матрице Гессе: если H(X)³0 для любого XÎRп, то функция выпуклая; если H(X)>0 для любого XÎRп, то функция строго выпуклая. 3.3.1.Пусть значения переменных линейной функции f(x1, x2, …, xn)= a1x1+a2x2+…+anxn меняются пропорционально (a1, a2, …, an) с коэффициентом пропорциональности a. Тогда при a>1 значения функции f(x1, x2, …, xn) возрастают, а при a<1 убывают. Упражнения. 3.4.1.Для функции f(x1, x2, x3): 1) Найти градиент в точке X0=( 2) Построить матрицу Гессе в точке X0. 3) Найти первый и второй дифференциалы в точке X0. 4) Найти стационарные точки. 5) Исследовать на выпуклость. а) f(x1, x2, x3)=-2 б) f(x1, x2, x3)=5 в) f(x1, x2, x3)= -2 г) f(x1, x2, x3)= -3 Решение. а.1) Найдём частные производные первого порядка:
Поэтому градиент Ñf(X0)= а.2) Для построения матрицы Гессе необходимо найти частные производные второго порядка:
Таким образом, матрица Гессе H(X)= - постоянная. Поэтому H(X0)= а.3) Первый дифференциал: df(X)= =(-4x1+4x2)dx1+(4x1-10x2+4x3)dx2+(4x3-4x2)dx3. То есть df(X0)= df(X0)=-8dx1+18dx2-8dx3. Второй дифференциал: d2f(X)= = Поэтому d2f(X0)=-4 а.4) Стационарными точками являются решения системы
которая в нашем случае имеет вид
Так как определитель системы D= Не равен нулю, то система имеет единственное решение (0, 0, 0), то есть (0, 0, 0) - стационарная точка функции. а.5) Для исследования выпуклости исследуем на знакоопределённость матрицу Гессе функции. Имеем угловые миноры: D1=-4<0, D2=24>0, D3=-32<0 - - знакочередующиеся, начиная с отрицательного. Следовательно, H(X) - отрицательно определённая, то есть функция - вогнутая. Ответ: 1) Ñf(X0)=(-8, 18, -8)Т - градиент в X0=(1, -1, 1); 2) H(X0)= 3) df(X0)=-8dx1+18dx2-8dx3 - первый дифференциал в X0=(1, -1, 1); 4) d2f(X0)=-4 5) функция выгнутая. 3.4.2.Доказать утверждение3.3.1.
Поиск по сайту: |

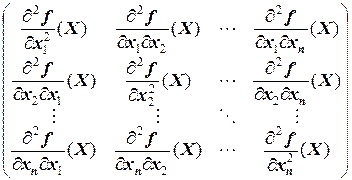 =
= ,
, , i, j=1, 2, …, n.
, i, j=1, 2, …, n.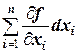 .
.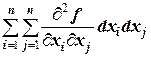
 =
= 
 =0 для всех i=1, 2, …, n.
=0 для всех i=1, 2, …, n.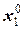 ,
, 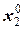 ,
,  ).
). -5
-5  -2
-2  +4х1х2+4х2х3, X0=(1, -1, 1);
+4х1х2+4х2х3, X0=(1, -1, 1); =-4x1+4x2,
=-4x1+4x2, 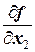 =-10x2+4x1+4x3,
=-10x2+4x1+4x3,  =-4x3+4x2;
=-4x3+4x2; .
. =-4,
=-4,  =-10,
=-10,  =-4,
=-4,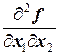 =
= 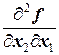 =4,
=4,  =
=  =0,
=0,  =
=  =-4.
=-4. -
-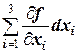 =
=  =
= +
+ 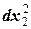 +
+ 
 +2
+2  dx1dx2+2
dx1dx2+2  dx1dx3+2
dx1dx3+2  dx2dx3
dx2dx3

 =-32
=-32 - матрица Гессе в X0=(1, -1, 1).
- матрица Гессе в X0=(1, -1, 1).