 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Системы линейных неравенств
Линейными называются неравенства вида a1x1+a2x2+…+anxn≥b (1.3) и a1x1+a2x2+…+anxn£b (1.4) Ясно, что из неравенства вида (1.3) к неравенству вида (1.4), и обратно, можно прийти умножением неравенства на -1. Поэтому под неравенством в общем виде будем иметь в виду, как правило, неравенство вида (1.3). Кроме того, очевидно, вместо нестрого знака ≥ или ≤ может стоять строгий > или <. Такие неравенства мы рассматривать не будем. Так что мы в дальнейшем будем иметь дело в основном с неравенствами вида (1.3). Практически все понятия, связанные с линейными уравнениями и их неравенствами дословно переносятся на линейные неравенства и их системы. В частности, упорядоченный набор (a1, a2, …an) называется решением системы (1.3), если неравенство a1a1+a2a2+…+anan≥b - верное, если рассматривается множество общих решений неравенств a11x1+a12x2+…+a1nxn≥b1, a21x1+a22x2+…+a2nxn≥b2, ………………………….. am1x1+am2x2+…+amnxn≥bm, то говорят, что они образуют систему:
Аналогично дословно переносятся понятия совместная и несовместная системы, определённая и неопределённая системы (хотя эти два понятия по определённым соображениям, которые мы опускаем, практически не применяются), равносильные системы, основная и расширенная матрица системы, столбец неизвестных и столбецсвободных членов. Что касается понятия элементарные преобразования системы линейных неравенств, то их мы практически применять не будем (при дословном переносе этих понятий, вообще говоря, при элементарных преобразованиях системы может получиться система, не равносильная данной). Ясно, что наряду с системами линейных уравнений и неравенств можно рассматривать смешанные системы, состоящие одновременно из уравнений и неравенств:
В нашем курсе нас будет интересовать в первую очередь системы с условиями неотрицательности неизвестных:
и т.д. Наконец, под линейными системами будем понимать, вообще говоря, смешанные системы, состоящие из линейных уравнений и (или) неравенств. В частности, они могут состоять только из уравнений или только неравенств. 1.2.1. Линейное неравенство вида (1.3) равносильно системе
а неравенство вида (1.4) равносильно системе
Отсюда получаем, что 1.2.2. Система вида (1.5) равносильна системе
Другими словами, система (1.5) приводится к системе (1.6) добавлением к левой части дополнительных неизвестных xn+1, xn+2, …, xn+m со знаком «-», а система
приводится к системе
добавлением к левой части дополнительных неизвестных со знаком «-». Очевидно, аналогично обстоит дело с любой смешанной системой, а также с системой, в которой имеются неравенства со знаком «≥» или «≤». Только в этих случаях в уравнения дополнительные неизвестные не добавляются, а в неравенства они добавляются с соответствующими знаками («+» или «-»). Например,
В любом случае, если исходная система состояла из m уравнений и неравенств с n неизвестными, то она приводится к системе уравнений с m+k неизвестными, из которых k неизвестных являются дополнительными, k≤m. В заключение раздела отметим, что при n=2 множество решений системы линейных неравенство образует обычный многоугольник (не исключено, что бесконечный), а при n=3 - обычный многогранник (не исключено, что он так же бесконечный). 1.3. Угловые и главные миноры. Миноры D1=a11, D2= 1.4. Собственные значения и собственные векторы. Пусть A=(aij)n´n - некоторая квадратная матрица. Собственным значением матрицыA, соответствующим ненулевому вектору X, называется число l такое, что AXT=lXT. При этом (ненулевой) вектор X называется собственным вектором матрицы А. 1.4.1. Число l0 является собственным значением матрицы A тогда и только тогда, когда оно является корнем многочлена j(l)=det(A-lE). Многочлен det(A-lE) называется характеристическим многочленом матрицы А. Уравнение det(A-lE)=0 - характеристическое уравнение матрицы А. Таким образом, для того, чтобы найти собственные значения матрицы А, достаточно решить его характеристическое уравнение
Множество всех корней характеристического уравнения матрицы совпадает с множеством всех её собственных значений. Заметим, что все собственные значения симметрической матрицы являются действительными. 1.4.2. Для нахождения собственного вектора X=(x1, x2, …, xn) матрицы A, соответствующего собственному значению l, достаточно решить систему
Множество ненулевых решений этой системы образует множество собственных векторов матрицы A.
Поиск по сайту: |
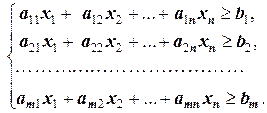 (1.5)
(1.5)
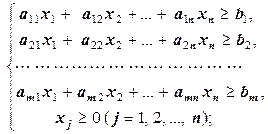


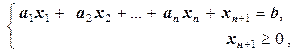 .
.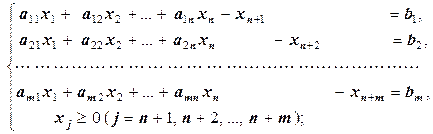 (1.6)
(1.6)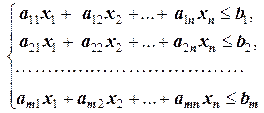

 Û
Û 
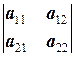 , …, Dn=
, …, Dn= 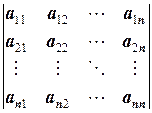 квадратной матрицы A=(aij)n´n называются угловыми минорами. Определители m-го порядка (m£n), получающиеся из определителя матрицы вычёркиванием каких-либо n-m строк и n-m столбцов с одинаковыми номерами, называются главными минорами.
квадратной матрицы A=(aij)n´n называются угловыми минорами. Определители m-го порядка (m£n), получающиеся из определителя матрицы вычёркиванием каких-либо n-m строк и n-m столбцов с одинаковыми номерами, называются главными минорами. =0. (1.7)
=0. (1.7) (1.8)
(1.8)