 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Указания к выполнению заданий и контрольных работСтр 1 из 7Следующая ⇒
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СБОРНИК ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
По разделам: «Физические основы механики», «Молекулярная физика и термодинамика»
Уфа 2004
Министерство образования Российской Федерации УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СБОРНИК ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ По разделам: «Физические основы механики», «Молекулярная физика и термодинамика» Уфа 2004 Министерство образования Российской Федерации УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра общей физики
СБОРНИК ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
по разделам: «Физические основы механики», «Молекулярная физика и термодинамика»
Уфа 2004 Составители: С.А. Шатохин, Е.В. Трофимова, Г.П. Михайлов
УДК [531+539.19](07)
ББК [22.2+22.36](Я7)
Сборник индивидуальных заданий по разделам курса общей физики «Физические основы механики», «Молекулярная физика и термодинамика». / Уфимск. гос. авиац. техн. ун-т; Сост.: С.А. Шатохин, Е.В. Трофимова, Г.П. Михайлов. – Уфа, 2004. - 61 с.
Приведены задачи по физическим основам механики, физике колебаний и волн, молекулярной физике и термодинамике и дан список индивидуальных заданий. Сборник предназначен для самостоятельной работы студентов дневного отделения и контрольных работ студентов заочного отделения, изучающих I раздел курса общей физики.
Табл.8. Библиогр.: 3 назв.
Рецензенты: А.С. Краузе Э.З. Якупов
© Уфимский государственный авиационный
технический университет, 2004 Содержание Введение......................................................................................................... 4 Указания к выполнению заданий и контрольных работ........................ 5 1. Кинематика................................................................................................ 6 2. Динамика материальной точки............................................................ 11 3. Динамика вращательного движения.................................................. 21 4. Элементы специальной теории относительности............................ 26 5. Механические колебания и волны...................................................... 29 6. Молекулярно-кинетическая теория идеальных газов.................... 41 7. Основы термодинамики........................................................................ 45 8. Реальные газы, жидкости и твердые тела.......................................... 52 Литература................................................................................................... 56 Индивидуальные задания.......................................................................... 57 Приложение................................................................................................. 60
Введение В сборнике подобраны задачи по разделам: «Физические основы механики», «Молекулярная физика и термодинамика» курса общей физики, предназначенные для самостоятельной работы студентов – выполнения домашних заданий и контрольных работ. Содержание задач направлено на формирование у студентов знаний физических явлений, законов, формул, единиц измерения физических величин, умения применять законы для решения качественных и расчетных задач, графически представить физические явления и законы, анализировать их. Решение задач формирует навыки самостоятельного мышления. Самостоятельная работа студентов поможет им при подготовке к экзамену, и будет способствовать более глубокому изучению данного раздела курса общей физики. Указания к выполнению заданий и контрольных работ. Номера вариантов и темы заданий определяет преподаватель. К выполнению индивидуальных занятий (или контрольных работ для заочников) рекомендуется приступать после изучения материала, соответствующего данному разделу программы, внимательного ознакомления с примерами решения задач, приведенных в методических указаниях по данному разделу (см. «Механика». Методические указания к практическим занятиям по курсу общей физики: УГАТУ, Сост. Е.В. Трофимова, Уфа, 2003). Задания и контрольные работы выполняются в обычной школьной тетради, на обложке которой приводятся сведения: - для очного отделения – Фамилия И.О. студента, группа, индивидуальные задания по физике по I части; - для заочного отделения – студент … факультета заочного отделения УГАТУ, группа, Фамилия И.О., адрес, контрольная работа № 1. Для замечаний преподавателя в тетради оставляются поля. Каждая следующая задача должна начинаться с новой страницы. Условия задач переписываются полностью, без сокращений. В решении необходимо указать основные законы и формулы, на которых базируется решение задачи, дать словесную формулировку этих законов, разъяснить смысл символов, употребляемых в записи формул. Если при решении задачи применяется формула, справедливая для частного случая, не выражающая какой-либо физический закон или не являющаяся определением физической величины, то ее следует вывести. Во всех случаях, когда это возможно, должен быть представлен чертеж, поясняющий задачу. Решение задачи должно сопровождаться краткими, но исчерпывающими пояснениями. Результат должен быть получен в общем виде, сделана проверка, дает ли рабочая формула правильную размерность искомой величины, подставлены числовые данные и получен окончательный числовой результат. Все величины, входящие в условие задачи, выразить в единицах одной системы (преимущественно СИ) и для наглядности выписать столбиком.
Кинематика Скорость и ускорение прямолинейного движения в общем случае определяются формулами
В случае прямолинейного равномерного движения
В случае прямолинейного равнопеременного движения
В этих уравнениях ускорение a положительно при равноускоренном движении и отрицательно при равнозамедленном. При криволинейном движении полное ускорение
Здесь aτ – тангенциальное (касательное) ускорение и an – нормальное (центростремительное) ускорение, причем
где υ – скорость движения и R – радиус кривизны траектории в данной точке. При вращательном движении в общем случае угловая скорость и угловое ускорение находятся по формулам
В случае равномерного вращательного движения угловая скорость
где Т – период вращения, n – частота вращения, т.е. число оборотов в единицу времени. Угловая скорость ω связана с линейной скоростью υ соотношением υ= ωR. Тангенциальное и нормальное ускорения при вращательном движении могут быть выражены в виде aτ=εR, an=ω2R.
1. 1. Капля дождя при скорости ветра υ = 11 м/с падает под углом α = 30° к вертикали. Определить, при какой скорости ветра υ2 капля будет падать под углом β = 45°. Ответ: 19 м/с. 1. 2. Два автомобиля, выехав одновременно из одного пункта, движутся прямолинейно в одном направлении. Зависимость пройденного ими пути задается уравнениями s1 = At + Bt2 и s2 = Ct + Dt2 + Ft3. Определить относительную скорость u автомобилей. Ответ: u = А– С+ 2(B–D)t–3Ft2. 1. 3. Велосипедист проехал первую половину времени своего движения со скоростью υ1 = 16 км/ч, вторую половину времени — со скоростью υ2 = 12 км/ч. Определить среднюю скорость движения велосипедиста. Ответ: 14 км/ч. 1. 4. Велосипедист проехал первую половину пути со скоростью υ1 = 16 км/ч, вторую половину пути — со скоростью υ2 = 12 км/ч. Определить среднюю скорость движения велосипедиста. Ответ: 13,7 км/ч. 1. 5. Студент проехал половину пути на велосипеде со скоростью υ1=16 км/ч. Далее половину оставшегося времени он ехал со скоростью υ2 = 12 км/ч, а затем до конца пути шел пешком со скоростью υ3 = 5 км/ч. Определить среднюю скорость движения студента на всем пути. Ответ: <υ> = 11,1 км/ч. 1. 6. В течение времени τ скорость тела задается уравнением вида υ = А + Bt + Сt2 (0≤ t ≤τ). Определить среднюю скорость за промежуток времени τ. Ответ: 1. 7. При падении камня в колодец его удар о поверхность воды доносится через t=5 с. Принимая скорость звука υ = 330 м/с, определить глубину колодца. Ответ: 109 м. 1. 8. Тело падает с высоты h=1 км с нулевой начальной скоростью. Пренебрегая сопротивлением воздуха, определить, какой путь пройдет тело: 1) за первую секунду своего падения; 2) за последнюю секунду своего падения. Ответ: 1) 4,9м; 2) 132 м. 1. 9. Тело падает с высоты h=1 км с нулевой начальной скоростью. Пренебрегая сопротивлением воздуха, определить, какое время понадобится телу для прохождения: 1) первых 10 м своего пути; 2) последних 10 м своего пути. Ответ: 1) 1,43 с; 2) 0,1 с. 1. 10.Тело брошено под углом к горизонту. Оказалось, что максимальная высота подъема h= 1. 11.Тело брошено со скоростью υo= 15 м/с под углом α=30° к горизонту. Пренебрегая сопротивлением воздуха, определить: 1) высоту h подъема тела; 2) дальность полета (по горизонтали) s тела; 3) время его движения. Ответ: 1) 2,87 м; 2) 19,9 м; 3) 1,53 с. 1. 12.Тело брошено со скоростью υo = 20 м/с под углом α=30° к горизонту. Пренебрегая сопротивлением воздуха, определить для момента времени t=1,5 с после начала движения: 1) нормальное ускорение; 2) тангенциальное ускорение. Ответ: 1) 9,47 м/с2; 2) 2,58 м/с2. 1. 13.С башни высотой h=40 м брошено тело со скоростью υo =20 м/с под углом α=45° к горизонту. Пренебрегая сопротивлением воздуха, определить: 1) время t движения тела; 2) на каком расстоянии s от основания башни тело упадет на Землю; 3) скорость υ падения тела на Землю; 4) угол φ, который составит траектория тела с горизонтом в точке его падения. Ответ: 1) 4,64 с; 2) 65,7 м; 3) 34,4 м/с; 4) 65,7°. 1. 14.Тело брошено горизонтально со скоростью υo = 15 м/с. Пренебрегая сопротивлением воздуха, определить радиус кривизны траектории тела через t= 2 с после начала движения. Ответ: 102 м. 1. 15.С башни высотой h = 30 м в горизонтальном направлении брошено тело с начальной скоростью υo = 10 м/с. Определить: 1) уравнение траектории тела у(х); 2) скорость υ тела в момент падения на Землю; 3) угол φ, который образует эта скорость с горизонтом в точке его падения. Ответ: 1) у = 1. 16.Зависимость пройденного телом пути от времени задается уравнением s = A–Bt + Ct2 + Dt3 (A = 6 м, В=3 м/с, С=2 м/с2, D=l м/с3). Определить для тела в интервале времени от t1 = 1 с до t2=4 с: 1) среднюю скорость; 2) среднее ускорение. Ответ: 1) 28 м/с; 2) 19 м/с2. 1. 17.Зависимость пройденного телом пути от времени задается уравнением s = А + Bt + Ct2 + Dt3 (С = 0,1 м/с2, D = 0,03 м/с3). Определить: 1) через сколько времени после начала движения ускорение а тела будет равно 2 м/с2; 2) среднее ускорение <а> тела за этот промежуток времени. Ответ: 1) 10 с; 2) 1,1 м/с2. 1. 18.Тело движется равноускоренно с начальной скоростью υo. Определить ускорение тела, если за время t = 2 c оно прошло путь s = 16 м и его скорость υ = 3 υo. Ответ: 4 м/с2. 1. 19.Материальная точка движется вдоль прямой так, что ее ускорение линейно растет, и за первые 10 c достигает значения 5 м/с3. Определить в конце десятой секунды: 1) скорость точки; 2) пройденный точкой путь. Ответ: 1) 25 м/с; 2) 83,3 м. 1. 20.Кинематические уравнения движения двух материальных точек имеют вид x1 = A1t + B1t2 + C1t3 и x2 = A2t + В2t2 + С2t3, где В1 = 4 м/с2, C1 = –3 м/с3, В2 = –2 м/с2, С2 = 1 м/с3. Определить момент времени, для которого ускорения этих точек будут равны. Ответ: 0,5 с. 1. 21.Кинематические уравнения движения двух материальных точек имеют вид x1 = A1+B1t+C1t2 и x2 = A2+В2 t + С2 t 2, где С1 = –2 м/с2, С2 = 1 м/с2. Определить: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения а1 и а2 для этого момента. Ответ: 1) 0; 2) а1 = –4 м/с2, а2=2 м/с2. 1. 22.Нормальное ускорение точки, движущейся по окружности радиусом r = 4 м, задается уравнением аn = А + Bt + Ct2 (А=1 м/с2, В = 6 м/с3, С = 9 м/с4). Определить: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время t1 = 5 с после начала движения; 3) полное ускорение для момента времени t2 = 1 с. Ответ: 1) 6 м/с2; 2) 85 м; 3) 6,32 м/с2. 1. 23.Зависимость пройденного телом пути s от времени t выражается уравнением s = At – Bt2 + Ct3 (A = 2 м/с, В=3 м/с2, С=4 м/с3). Записать выражения для скорости и ускорения. Определить для момента времени t = 2 с после начала движения: 1) пройденный путь; 2) скорость; 3) ускорение. Ответ: 1) 24 м; 2) 38 м/с; 3) 42 м/с2. 1. 24.Зависимость пройденного телом пути по окружности радиусом r = 3 м задается уравнением s = At2 + Bt (A = 0,4 м/с2, В = 0,1 м/с). Определить для момента времени t = 1 с после начала движения ускорения: 1) нормальное; 2) тангенциальное; 3) полное. Ответ: 1) 0,27 м/с2; 2) 0,8 м/с2; 3) 0,84 м/с2. 1. 25.Радиус-вектор материальной точки изменяется со временем по закону r = t3i + 3t2j, где i, j — орты осей х и у. Определить для момента времени t = 1 с: 1) модуль скорости; 2) модуль ускорения. Ответ: 1) 6,7 м/с; 2) 8,48 м/с2. 1. 26.Радиус-вектор материальной точки изменяется со временем по закону r=4t2i+3tj+2k. Определить: 1) скорость υ; 2) ускорение а; 3) модуль скорости в момент времени t = 2 с. Ответ: 3) 16,3 м/с. 1. 27.Материальная точка начинает двигаться по окружности радиусом r = 12,5 см с постоянным тангенциальным ускорением аτ = 0,5 см/с2. Определить: 1) момент времени, при котором вектор ускорения a образует с вектором скорости υ угол α = 45°; 2) путь, пройденный за это время движущейся точкой. Ответ: 1) 5 с; 2) 6,25 см. 1. 28.Линейная скорость υ1 точки, находящейся на ободе вращающегося диска, в три раза больше, чем линейная скорость υ2 точки, находящейся на 6 см ближе к его оси. Определить радиус диска. Ответ: 9 см. 1. 29.Колесо вращается с постоянным угловым ускорением ε = 3 рад/с2. Определить радиус колеса, если через t = 1 с после начала движения полное ускорение колеса а = 7,5 м/с2. Ответ: 79 см. 1. 30. Найти линейную скорость υ вращения точек земной поверхности на широте Санкт-Петербурга (φ = 60о). Ответ: 231 м/с. 1. 31.Якорь электродвигателя, имеющий частоту вращения n=50 с-1, после выключения тока, сделав N = 628 оборотов, остановился. Определить угловое ускорение ε якоря. Ответ: 12,5 рад/с2. 1. 32.Колесо автомашины вращается равнозамедленно. За время t = 2 мин оно изменило частоту вращения от 240 до 60 мин-1. Определить: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время. Ответ: 1) 0,157 рад/с2; 2) 300. 1. 33.Точка движется по окружности радиусом R = 15 см с постоянным тангенциальным ускорением аτ. К концу четвертого оборота после начала движения линейная скорость точки υ= 15 см/с. Определить нормальное ускорение аn точки через t = 16 с после начала движения. Ответ: 1,5 см/с2. 1. 34.Диск радиусом R = 10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = A+Вt+Ct2+Dt3 (В = 1 рад/с, С = 1 рад/с2, D = 1 рад/с3). Определить для точек на ободе диска к концу второй секунды после начала движения: 1) тангенциальное ускорение aτ; 2) нормальное ускорение аn; 3) полное ускорение а. Ответ: 1) 1,4м/с2; 2) 28,9 м/с2; 3) 28,9 м/с2. 1. 35.Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = At2 (A = 0,1 рад/с2). Определить полное ускорение а точки на ободе диска к концу второй секунды после начала движения, если линейная скорость этой точки в этот момент υ = 0,4 м/с. Ответ: 0,26 м/с2. 1. 36.Диск радиусом R = 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением υ = At + Bt2 (A = 0,3 м/с2, B = 0,1 м/с3). Определить момент времени, для которого вектор полного ускорения a образует с радиусом колеса угол φ = 4°. Ответ: 2 с. 1. 37.Во сколько раз нормальное ускорение аn точки, лежащей на ободе вращающегося колеса, больше ее тангенциального ускорения аτ для того момента, когда вектор полного ускорения точки составляет угол α = 30о с вектором ее линейной скорости? Ответ: аn/аτ = 0,58.
Поиск по сайту: |

 .
.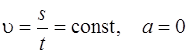 .
. .
. .
. ,
,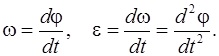

 .
. (s — дальность полета). Пренебрегая сопротивлением воздуха, определить угол броска к горизонту. Ответ: 45°.
(s — дальность полета). Пренебрегая сопротивлением воздуха, определить угол броска к горизонту. Ответ: 45°.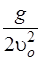 х2; 2) 26,2 м/с; 3) 67,8°.
х2; 2) 26,2 м/с; 3) 67,8°.