 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Сложение однонаправленных колебаний одинаковой частоты
Задача сложения нескольких колебаний может возникнуть, например, в оптике, где световые колебания (колебания вектора напряженности электрического поля) в некоторой точке определяются как результат наложения многих колебаний, приходящих в данную точку от различных участков волнового фронта. Под сложением колебаний понимают нахождение результирующих колебаний системы в тех случаях, когда эта система одновременно участвует в нескольких колебательных процессах. Различают два предельных случая: · сложение колебаний одинакового направления; · сложение взаимно перпендикулярных колебаний. Рассмотрим первый случай – сложение двух гармонических колебаний одинакового направления и частоты. Для сложения колебаний удобно применять метод векторных диаграмм. Суть этого метода в том, что гармоническое колебание представляется при помощи вектора, длина которого равна амплитуде колебания, а направление вектора образует с осью OX угол, равный фазе колебания. Амплитуда и начальная фаза результирующего колебания определяются при помощи векторного сложения. Допустим, что требуется сложить два гармонических колебания: Рис. 6.4.1. Сложение комплексных векторов на диаграмме
Этот вектор в плоскости диаграммы вращается с той же частотой Выделим три характерных случая. · Если разность начальных фаз · Если разность фаз · Если частоты складываемых колебаний не одинаковы, то результирующий вектор пульсирует по величине и вращается с непостоянной скоростью. В этом случае результирующее колебание не будет гармоническим и описывается другими более сложными зависимостями. 3.2 Сложное колебание и его гармонический спектр. Сложение колебаний приводит к более сложным формам колебаний. Для практических целей бывает необходимой противоположная операция: разложение сложного колебания на простые, обычно гармонические, колебания. Фурье показал, что периодическая функция любой сложности может быть представлена в виде суммы гармонических функций, частоты которых кратны частоте сложной периодической функции. Такое разложение периодической функции на гармонические и, следовательно, разложение различных периодичных процессов (механические, электрические, и т.п.) на гармонические колебания называется гармоническим анализом. Существуют математические выражения, которые позволяют найти составляющие гармонические функции. Автоматически гармонический анализ колебаний, в том числе и для целей медицины, осуществляется специальными приборами – анализаторами. Совокупность гармонических колебаний, на которое разложено сложное колебание, называется гармоническим спектром сложного колебания. Гармонический анализ позволяет достаточно детально описать и проанализировать любой сложный колебательный процесс, он находит применение в акустике, радиотехнике, электронике, и других областях науки и техники. 3.3 Сложение взаимно перпендикулярных колебаний Рассмотрим сложение взаимно перпендикулярных колебаний на примере механических колебаний. Допустим, что материальная точка может совершать колебания как вдоль оси Оx, так и вдоль перпендикулярной к ней оси Оy. Если возбудить оба колебания, материальная точка будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит от разности фаз обоих колебаний. Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна 0. Тогда уравнения колебаний запишутся следующим образом: поэтому Представим далее косинус во втором уравнении (6.5.1) по формуле для косинуса суммы, подставляя при этом вместо
1. Разность фаз равна нулю. В этом случае уравнение (6.5.4) примет вид: Рис. 6.5.1. Вид траектории для разности фаз, равной нулю
Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой Рис. 6.5.2. Вид траектории для разности фаз, равной π
Рис. 6.5.3. Вид траектории для разности фаз, равной ±π/2
3. При разности фаз равной ±p/2 уравнение (6.5.4) переходит в следующее т.е. в уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний A и B (см. рис 6.5.3). В этом случае говорят об эллиптически поляризованных колебаниях. При равенстве амплитуд (A=B) эллипс превращается в окружность. Колебания, описываемые уравнением (6.5.9) при (A=B) называются поляризованными по кругу или циркулярно поляризованными. Случаи разности фаз +p/2 и -p/2 отличаются направлением движения по эллипсу или по окружности. В первом случае тело движется по часовой стрелке, во втором – против часовой стрелки. Если теперь представить, что вместо колебаний материальной точки речь идет о колебаниях вектора напряженности электрического (или магнитного поля), то все изложенное в разделе 6.5 соответствует сложению двух колебаний поля, линейно поляризованных во взаимно перпендикулярных плоскостях. Результат такого сложения, наблюдаемый на экране осциллографа, имеет вид эллипса. Этот эллипс является одной из фигур Лиссажу. Более сложные фигуры Лиссажу (восьмерка, седло и т.д.) соответствуют сложению взаимно перпендикулярных колебаний кратных частот.
Поиск по сайту: |
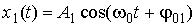 и
и  . (6.4.1)
. (6.4.1)
 Сложим соответствующие им векторы
Сложим соответствующие им векторы 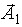 и
и 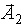 для момента времени t. Проекция результирующего вектора
для момента времени t. Проекция результирующего вектора 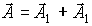 на ось Оx равна сумме проекций складываемых векторов
на ось Оx равна сумме проекций складываемых векторов 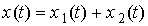 . Вектор
. Вектор 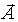 представляет собой векторное изображение результирующего колебания (см. рис.6.4.1).
представляет собой векторное изображение результирующего колебания (см. рис.6.4.1).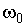 , с которой колеблются складываемые осциллирующие функции x1(t) и x2(t). Результирующая амплитуда
, с которой колеблются складываемые осциллирующие функции x1(t) и x2(t). Результирующая амплитуда  и начальная фаза
и начальная фаза 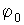 находятся геометрическим построением для момента времени t=0:
находятся геометрическим построением для момента времени t=0: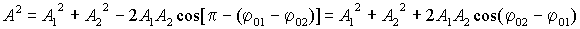 (6.4.2)
(6.4.2)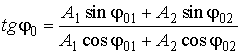 . (6.4.3)
. (6.4.3)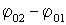 обоих колебаний равна 0 или 2pn, где n=1,2,…. то колебания находятся в фазе и амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний,
обоих колебаний равна 0 или 2pn, где n=1,2,…. то колебания находятся в фазе и амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний, 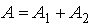 .
. , т.е. оба колебания находятся в противофазе, то
, т.е. оба колебания находятся в противофазе, то  (при
(при 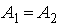 наблюдается полное гашение колебаний).
наблюдается полное гашение колебаний). и
и 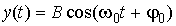 , (6.5.1)
, (6.5.1) – разность начальных фаз обоих колебаний. Выражения (6.5.1) представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (6.5.1) время. Из первого уравнения (6.5.1) следует, что
– разность начальных фаз обоих колебаний. Выражения (6.5.1) представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (6.5.1) время. Из первого уравнения (6.5.1) следует, что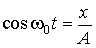 , (6.5.2)
, (6.5.2)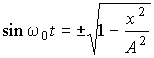 . (6.5.3)
. (6.5.3)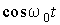 и
и 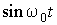 их значения из соотношений (6.5.2) и (6.5.3). В результате получим
их значения из соотношений (6.5.2) и (6.5.3). В результате получим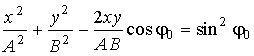 . (6.5.4)
. (6.5.4)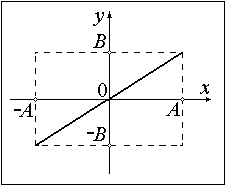 Уравнение (6.5.4) это уравнение эллипса, оси которого повернуты относительно координатных осей Ox и Oy. Ориентация эллипса и величина его полуосей зависят довольно сложным образом от амплитуд A и B и разности фаз
Уравнение (6.5.4) это уравнение эллипса, оси которого повернуты относительно координатных осей Ox и Oy. Ориентация эллипса и величина его полуосей зависят довольно сложным образом от амплитуд A и B и разности фаз 
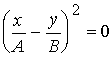 , (6.5.5)
, (6.5.5)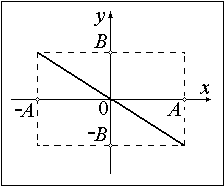 откуда получается уравнение прямой(см. рис. 6.5.1):
откуда получается уравнение прямой(см. рис. 6.5.1):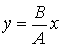 . (6.5.6)
. (6.5.6)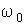 и амплитудой равной
и амплитудой равной 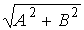 .
. 2. Разность фаз равна
2. Разность фаз равна  . В этом случае уравнение (6.5.4) примет вид:
. В этом случае уравнение (6.5.4) примет вид: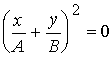 . (6.5.7)
. (6.5.7) Откуда получается, что результирующее движение представляет собой гармоническое колебание вдоль прямой (см. рис. 6.5.2):
Откуда получается, что результирующее движение представляет собой гармоническое колебание вдоль прямой (см. рис. 6.5.2):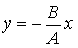 . (6.5.8)
. (6.5.8) Движения, описываемые формулами (6.5.6) и (6.5.8) называют линейно поляризованными колебаниями.
Движения, описываемые формулами (6.5.6) и (6.5.8) называют линейно поляризованными колебаниями. , (6.5.9)
, (6.5.9)