 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Параллельное соединение индуктивно связанных элементов цепи
Предположим, что две индуктивно связанные катушки соединены параллельно. Их параметры соответственно равны: активные сопротивления r1 и r2, индуктивности L1 и L2 и взаимной индуктивностью М. Возможны два вида их соединения – согласное и встречное.
4.3.1. Согласное включение
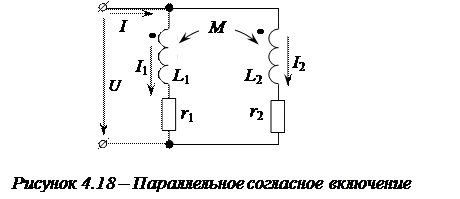
Одноименные зажимы подключены к одному узлу (рис. 4.18). При положительных направлениях токов и напряжений, указанных на рисунке 4.18, на основании законов Кирхгофа имеем:
При положительных направлениях токов и напряжений, указанных на рисунке 4.18, на основании законов Кирхгофа имеем:
где Решив эти уравнения, получаем
откуда следует, что входное сопротивление цепи При согласном включении и равных полных сопротивлениях
откуда следует, что входное сопротивление цепи Таким образом, при согласном включении и равенстве полных сопротивлений, ток будет меньше, чем при отсутствии индуктивной связи.
При Векторная диаграмма при согласном включении, приведена на рисунке 4.19.
Пример 4.9.Цепь состоит из двух одинаковых индуктивно связанных катушек, соединенных параллельно (рис. 4.18), с параметрами r1 = r2 = r = 40 Ом, x1 = x2 = x = 60 Ом, xM = 50 Ом, u = 100 В. Требуется рассчитать токи и напряжения на каждой катушке, ток в неразветвленном участке цепи, построить векторную диаграмму. Решение. 1. Определяем сопротивление взаимной индукции:
2. Определяем сопротивление каждой индуктивно связанной катушки:
3. Определяем входное сопротивление цепи:
4. Ток в цепи
5. Токи в параллельных ветвях
6. Определяем комплексы напряжений на каждом элементе цепи:
Рисунок 4.20 – Векторная диаграмма при согласном включении двух одинаковых катушек
Пример 4.10.Цепь состоит из двух индуктивно связанных катушек, соединенных параллельно (рис. 4.18), с параметрами r1 = 30 Ом, x1 = 60 Ом, r2 = 100 Ом, x2 = 40 Ом, xM = 20 Ом, u = 100 В. Требуется рассчитать ток и напряжения на каждой катушке, построить векторную диаграмму. Решение. 1. Определяем сопротивление взаимной индукции:
2. Определяем сопротивление каждой индуктивно связанной катушки:
3. Определяем входное сопротивление цепи:
4. Ток в цепи
5. Токи в параллельных ветвях
6. Определяем комплексы напряжений на каждом элементе цепи:
Рисунок 4.21 – Векторная диаграмма при согласном включении двух катушек
4.3.2. Встречное включение
Рассмотрим пример встречного включения. Одноименные зажимы присоединены к разным узлам, т.е. L1 и L2 присоединены к узлу разноименными зажимами (рис. 4.22). тогда положительные направления напряжений взаимной индукции и токов, ориентированы относительно одноименных зажимов неодинаково.
При положительных направлениях токов и напряжений, указанных на рисунке 4.22, на основании законов Кирхгофа имеем:
Решив эти уравнения, получаем
откуда следует, что входное сопротивление цепи
При встречном включении и равных полных сопротивлениях
откуда следует, что входное сопротивление цепи Таким образом, при согласном включении и равенстве полных сопротивлений, ток будет больше, чем при отсутствии индуктивной связи. Векторная диаграмма при согласном включении, приведена на рисунке 4.23.
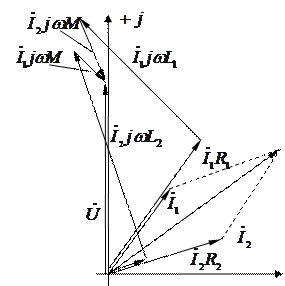
Рисунок 4.23 – Векторная диаграмма при встречном включении
Пример 4.11.Цепь состоит из двух одинаковых индуктивно связанных катушек, соединенных параллельно (рис. 4.22), с параметрами r1 = r2 = r = 40 Ом, x1 = x2 = x = 60 Ом, xM = 50 Ом, u = 100 В. Требуется рассчитать токи и напряжения на каждой катушке, ток в неразветвленном участке цепи, построить векторную диаграмму. Решение. 1. Определяем сопротивление взаимной индукции:
2. Определяем сопротивление каждой индуктивно связанной катушки:
3. Определяем входное сопротивление цепи:
4. Ток в цепи
5. Токи в параллельных ветвях
6. Определяем комплексы напряжений на каждом элементе цепи:
Рисунок 4.24 – Векторная диаграмма при согласном включении двух одинаковых катушек
Пример 4.12.Цепь состоит из двух индуктивно связанных катушек, соединенных параллельно (рис. 4.18), с параметрами r1 = 30 Ом, x1 = 60 Ом, r2 = 100 Ом, x2 = 40 Ом, xM = 20 Ом, u = 100 В. Требуется рассчитать ток и напряжения на каждой катушке, построить векторную диаграмму. Решение. 1. Определяем сопротивление взаимной индукции:
2. Определяем сопротивление каждой индуктивно связанной катушки:
3. Определяем входное сопротивление цепи:
4. Ток в цепи
5. Токи в параллельных ветвях
6. Определяем комплексы напряжений на каждом элементе цепи:
Рисунок 4.25 – Векторная диаграмма при согласном включении двух катушек
4.3.3. Мощность при параллельном соединении индуктивно связанных катушек
Комплексная мощность на зажимах цепи в общем случае равна
Баланс активной мощности имеет вид
а реактивной – Необходимо отметить, что коэффициент мощности при согласном включении уменьшается, т.к. реактивная мощность При встречном включении коэффициент мощности увеличивается, т.к. реактивная мощность уменьшается на величину Однако суммарная мощность имеет индуктивный характер, т.к.
Рассмотрим комплексные мощности, потребляемые каждой параллельной ветвью:
Баланс активной мощности в этом случае имеет вид
Здесь Необходимо отметить, что абсолютные величины передаваемой электромагнитным путем мощности, равны Комплексная мощность, передаваемая электромагнитным путем от первой катушки ко второй
Проанализируем полученный результат. Если индуктивно связанные катушки одинаковые, то Если При встречном включении Если
Пример 4.13.Составим баланс активных и реактивных мощностей для электрической цепи, представленной на рисунке 4.18 и рассмотренной в примере 4.9. Из примера 4.9, следует, что комплекс напряжения на источнике пита-ния
1. Определяем активную и реактивную мощности, генерируемые источником питания.
Таким образом, суммарная активная 2. Определяем активную мощность, потребляемую потребителями
Имеет место баланс активных мощностей. 3. Определим реактивную мощность, потребляемую потребителями
Имеет место баланс реактивных мощностей.
Пример 4.14.Составим баланс активных и реактивных мощностей для электрической цепи, представленной на рисунке 4.18 и рассмотренной в примере 4.10. Из примера 4.10, следует, что комплекс напряжения на источнике пита-ния 1. Определяем активную и реактивную мощности, генерируемые источником питания.
Таким образом, суммарная активная 2. Комплексные мощности, потребляемые каждой параллельной ветвью:
Таким образом, суммарная активная мощность ветвей 3. Определяем активную мощность, потребляемую потребителями
На резистивных элементах
Суммарная активная мощность
4. Комплексная мощность, передаваемая электромагнитным путем от первой катушки ко второй
Значит, активная мощность передается от второй катушки к первой. 5. Баланс активных мощностей:
6. Определяем реактивную мощность, потребляемую потребителями
На индуктивных элементах
Суммарная реактивная мощность
7. Баланс реактивных мощностей:
Пример 4.15.Составим баланс активных и реактивных мощностей для электрической цепи, представленной на рисунке 4.22 и рассмотренной в примере 4.11.
Из примера 4.11, следует, что комплекс напряжения на источнике пита-ния 4. Определяем активную и реактивную мощности, генерируемые источником питания.
Таким образом, суммарная активная 5. Определяем активную мощность, потребляемую потребителями
Имеет место баланс активных мощностей. 6. Определим реактивную мощность, потребляемую потребителями
Имеет место баланс реактивных мощностей. Пример 4.16.Составим баланс активных и реактивных мощностей для электрической цепи, представленной на рисунке 4.22 и рассмотренной в примере 4.12. Из примера 4.12, следует, что комплекс напряжения на источнике пита-ния 1. Определяем активную и реактивную мощности, генерируемые источником питания.
Таким образом, суммарная активная 2. Комплексные мощности, потребляемые каждой параллельной ветвью:
Таким образом, суммарная активная мощность ветвей 3. Определяем активную мощность, потребляемую потребителями
На резистивных элементах
Суммарная активная мощность
4. Комплексная мощность, передаваемая электромагнитным путем от первой катушки ко второй
Таким образом, активная мощность передается от первой катушки ко второй. 5. Баланс активных мощностей:
6. Определяем реактивную мощность, потребляемую потребителями
На индуктивных элементах
Суммарная реактивная мощность
8. Баланс реактивных мощностей:
Поиск по сайту: |
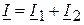
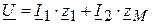
 ,
,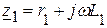 ,
, 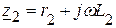 ,
, 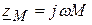 .
.

 ,
,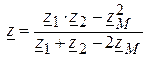 .
. :
: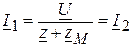 ,
,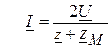 ,
, .
.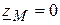 , т.е. при отсутствии индуктивной связи между ветвями, входное комплексное сопротивление имеет вид
, т.е. при отсутствии индуктивной связи между ветвями, входное комплексное сопротивление имеет вид 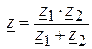 .
.
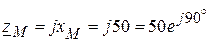 Ом.
Ом.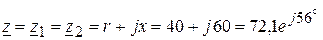 Ом.
Ом.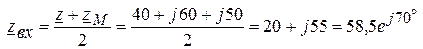 Ом.
Ом.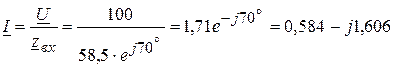 A.
A.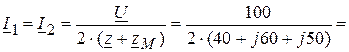
 А.
А.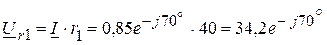 В,
В,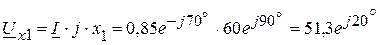 В,
В,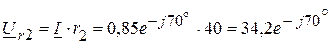 В,
В,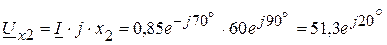 В,
В,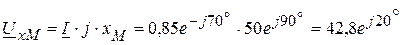 В.
В.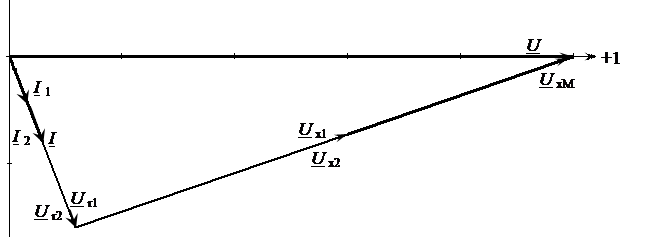
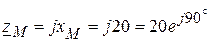 Ом.
Ом.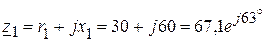 Ом,
Ом,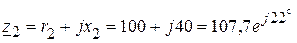 Ом.
Ом.
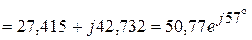 Ом.
Ом.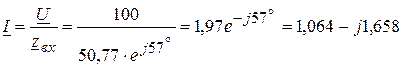 A.
A.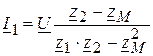

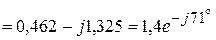 А,
А,
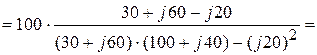
 А.
А.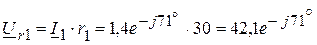 В,
В,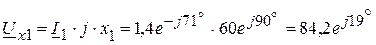 В,
В,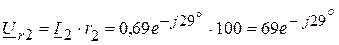 В,
В,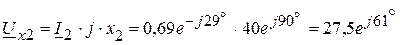 В,
В,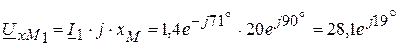 В.
В.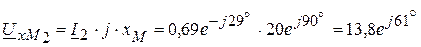 В
В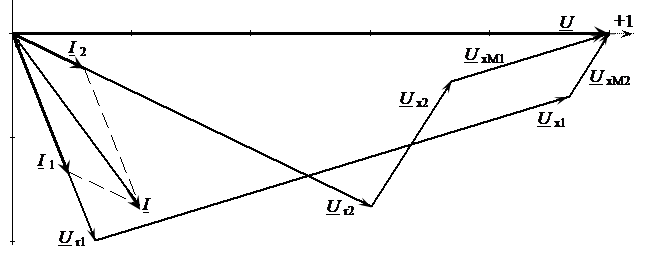


 .
.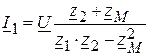
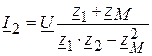
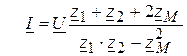 ,
, .
.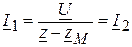 ,
,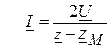 ,
,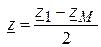 .
.
 Ом.
Ом. A.
A.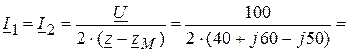
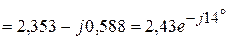 А.
А. В,
В,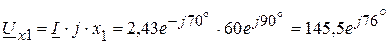 В,
В,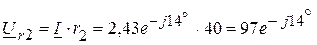 В,
В,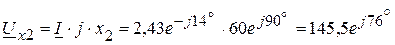 В,
В,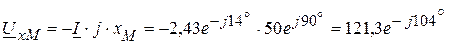 В.
В.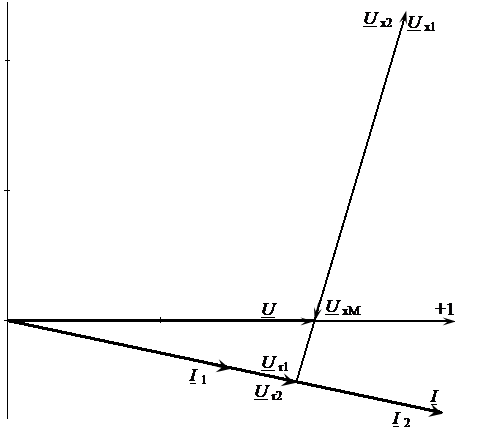

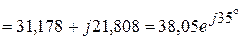 Ом.
Ом.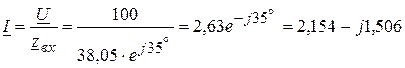 A.
A.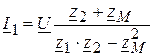
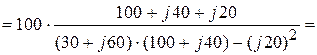
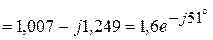 А,
А,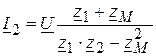
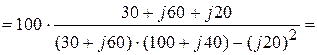
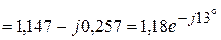 А.
А.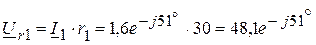 В,
В,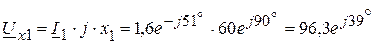 В,
В,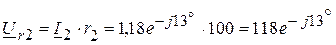 В,
В,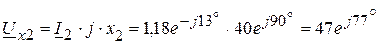 В,
В,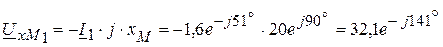 В.
В. В
В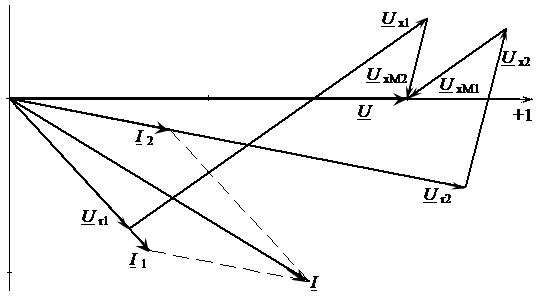
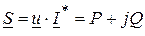 .
.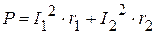 ,
,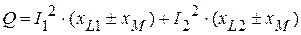 .
.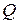 больше на величину магнитного поля взаимной индукции
больше на величину магнитного поля взаимной индукции  .
.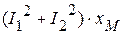 .
.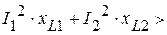
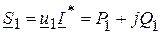 ,
,  .
. ,
,  .
.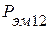 – активная мощность, передаваемая электромагнитным путем. Знак «+» означает, что мощность
– активная мощность, передаваемая электромагнитным путем. Знак «+» означает, что мощность 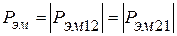 .
.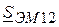
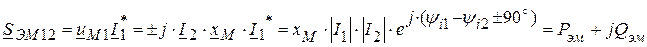
 и
и 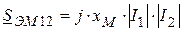 . Следовательно,
. Следовательно, 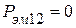 и активная мощность не передается электромагнитным путем.
и активная мощность не передается электромагнитным путем.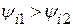 , то при согласном включении
, то при согласном включении  . Следовательно,
. Следовательно, 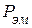 отрицательно, и электромагнитная мощность передается от второй катушки к первой.
отрицательно, и электромагнитная мощность передается от второй катушки к первой.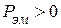 и активная мощность передается от первой катушки ко второй.
и активная мощность передается от первой катушки ко второй.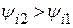 , то при согласном включении
, то при согласном включении 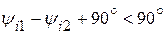 и активная электромагнитная мощность передается от второй катушки к первой.
и активная электромагнитная мощность передается от второй катушки к первой.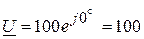 В, а комплексы токов
В, а комплексы токов 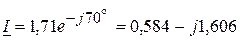 A,
A,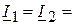
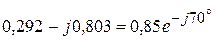 А.
А.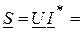
 ВА.
ВА.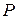 и суммарная реактивная
и суммарная реактивная 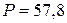 Вт,
Вт,  ВАр.
ВАр.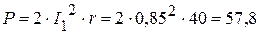 Вт,
Вт, ВАр.
ВАр.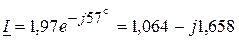 A,
A, 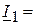
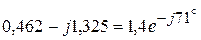 А,
А, 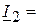
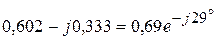 А.
А. ВА.
ВА.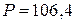 Вт,
Вт, 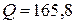 ВАр.
ВАр.
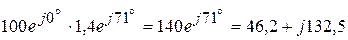 ВА,
ВА,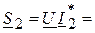
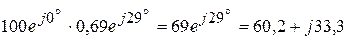 ВА.
ВА. Вт, а суммарная реактивная
Вт, а суммарная реактивная  ВАр.
ВАр.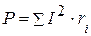 .
. Вт,
Вт, Вт.
Вт.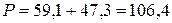 Вт.
Вт.
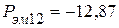 Вт,
Вт, 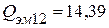 ВАр.
ВАр.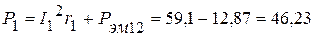 Вт,
Вт,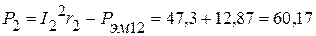 Вт.
Вт. .
.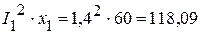 ВАр,
ВАр, ВАр.
ВАр.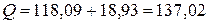 ВАр.
ВАр.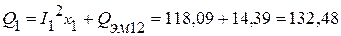 ВАр,
ВАр, ВАр.
ВАр. А,
А, 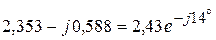 А.
А.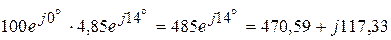 ВА.
ВА.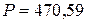 Вт,
Вт,  ВАр.
ВАр. Вт,
Вт,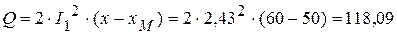 ВАр.
ВАр.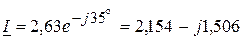 A,
A,  А,
А,  А.
А.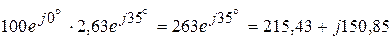 ВА.
ВА.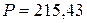 Вт,
Вт, 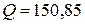 ВАр.
ВАр.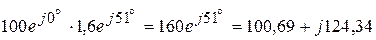 ВА,
ВА, ВА.
ВА.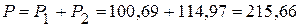 Вт, а суммарная реактивная
Вт, а суммарная реактивная 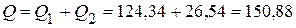 ВАр.
ВАр.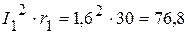 Вт,
Вт,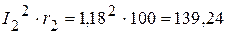 Вт.
Вт. Вт.
Вт.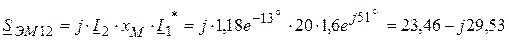
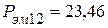 Вт,
Вт, 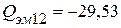 ВАр.
ВАр. Вт,
Вт,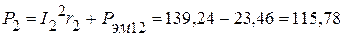 Вт.
Вт.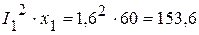 ВАр,
ВАр,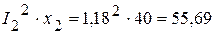 ВАр.
ВАр.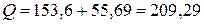 ВАр.
ВАр. ВАр,
ВАр,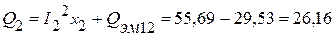 ВАр.
ВАр.