 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
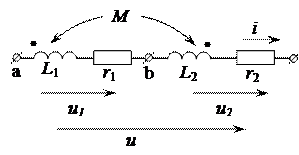
Последовательное соединение индуктивно связанных элементов цепи
Предположим, что две индуктивно связанные катушки соединены последовательно. Их параметры соответственно равны: активные сопротивления r1 и r2, индуктивности L1 и L2 и взаимной индуктивностью М. Возможны два вида их соединения – согласное и встречное.
4.2.1. Согласное включение
Рассмотрим согласное включение индуктивно связанных катушек (рис. 4.8).
Напряжения на зажимах цепи, согласно второго закона Кирхгофа, равно
где В результате
Из полученного выражения следует, что полное сопротивление при согласном включении больше, чем при отсутствии индуктивной связи за счет увеличения реактивного сопротивления на величину Векторная диаграмма при согласном включении, приведена на рисунке 4.9.
Пример 4.1.Цепь состоит из двух одинаковых индуктивно связанных катушек, соединенных последовательно (рис. 4.8), с параметрами r1 = r2 = r = 40 Ом, x1 = x2 = x = 60 Ом, xM = 50 Ом, u = 100 В. Требуется рассчитать ток и напряжения на каждой катушке, построить векторную диаграмму. Решение. 1. Определяем сопротивление взаимной индукции:
2. Определяем сопротивление каждой индуктивно связанной катушки:
3. Определяем входное сопротивление цепи:
4. Ток в цепи
5. Определяем комплексы напряжений на каждом элементе цепи:
6. Определяем комплексы напряжений на участках цепи:
Рисунок 4.10 – Векторная диаграмма при согласном включении двух одинаковых катушек Пример 4.2.Цепь состоит из двух индуктивно связанных катушек, соединенных последовательно (рис. 4.8), с параметрами r1 = 30 Ом, x1 = 60 Ом, r2 = 100 Ом, x2 = 40 Ом, xM = 20 Ом, u = 100 В. Требуется рассчитать ток и напряжения на каждой катушке, построить векторную диаграмму. Решение. 1. Определяем сопротивление взаимной индукции:
2. Определяем сопротивление каждой индуктивно связанной катушки:
3. Определяем входное сопротивление цепи:
4. Ток в цепи
5. Определяем комплексы напряжений на каждом элементе цепи:
6. Определяем комплексы напряжений на участках цепи:
Рисунок 4.13 – Векторная диаграмма при согласном включении двух катушек
4.2.2. Встречное включение
Напряжения на зажимах цепи, согласно второго закона Кирхгофа, равно
где В результате
где Из полученного выражения следует, что полное сопротивление при встречном включении уменьшается на величину Векторная диаграмма при встречном включении, приведена на рисунке 4.15.
Пример 4.3. Цепь состоит из двух одинаковых индуктивно связанных катушек, соединенных последовательно (рис. 4.14), с параметрами r1 = r2 = r = 40 Ом, x1 = x2 = x = 60 Ом, xM = 50 Ом, u = 100 В. Требуется рассчитать ток и напряжения на каждой катушке, построить векторную диаграмму. Решение. 1. Определяем сопротивление взаимной индукции:
2. Определяем сопротивление каждой индуктивно связанной катушки:
3. Определяем входное сопротивление цепи:
4. Ток в цепи
5. Определяем комплексы напряжений на каждом элементе цепи:
6. Определяем комплексы напряжений на участках цепи:
Рисунок 4.16 – Векторная диаграмма при встречном включении двух одинаковых катушек
Пример 4.4. Цепь состоит из двух индуктивно связанных катушек, соединенных последовательно (рис. 4.14), с параметрами r1 = 30 Ом, x1 = 60 Ом, r2 = 100 Ом, x2 = 40 Ом, xM = 20 Ом, u = 100 В. Требуется рассчитать ток и напряжения на каждой катушке, построить векторную диаграмму. Решение. 7. Определяем сопротивление взаимной индукции:
8. Определяем сопротивление каждой индуктивно связанной катушки:
9. Определяем входное сопротивление цепи:
10. Ток в цепи
11. Определяем комплексы напряжений на каждом элементе цепи:
12. Определяем комплексы напряжений на участках цепи:
Рисунок 4.17 – Векторная диаграмма при согласном включении двух катушек
4.2.3. Мощность при последовательном соединении индуктивно связанных катушек
При наличии индуктивных связей имеет место изменение энергетических соотношений за счет наличия магнитного потока, обеспечивающего индуктивную связь. Комплексная мощность при последовательном соединении в общем случае равна
Активная мощность Реактивная мощность При согласном включении результирующее поле возрастает за счет магнитного поля взаимной индукции
Баланс мощности в этом случае будет иметь вид:
где
Пример 4.5.Составим баланс активных и реактивных мощностей для электрической цепи, представленной на рисунке 4.8 и рассмотренной в примере 4.1. Из примера 4.1, следует, что комплекс напряжения на источнике пита-ния 1. Определяем активную и реактивную мощности, генерируемые источником питания.
Таким образом, суммарная активная 2. Определяем активную мощность, потребляемую потребителями
Имеет место баланс активных мощностей. 3. Определим реактивную мощность, потребляемую потребителями
Имеет место баланс реактивных мощностей.
Пример 4.6.Составим баланс активных и реактивных мощностей для электрической цепи, представленной на рисунке 4.8 и рассмотренной в примере 4.2. Из примера 4.2, следует, что комплекс напряжения на источнике пита-ния 1. Определяем активную и реактивную мощности, генерируемые источником питания.
Таким образом, суммарная активная 2. Определяем активную мощность, потребляемую потребителями
На резистивных элементах
Суммарная активная мощность
Имеет место баланс активных мощностей. 3. Определим реактивную мощность, потребляемую потребителями На индуктивных элементах
Суммарная реактивная мощность
Имеет место баланс реактивных мощностей.
При встречном включении поток взаимной индукции оказывает размагничивающее действие на основной поток. Величина реактивной мощности, потребляемая из сети, в этом случае равна
Реактивная мощность будет идти на создание магнитного поля, т.к.
Баланс мощности в этом случае имеет вид
Из вышеуказанного следует, что коэффициент мощности Рассмотрим энергетические соотношения между отдельно взятыми индуктивно связанными катушками. Комплексная мощность, потребляемая катушками, будет равна:
комплексная мощность первой катушки
а второй катушки – Необходимо отметить, что
Пример 4.7.Составим баланс активных и реактивных мощностей для электрической цепи, представленной на рисунке 4.14 и рассмотренной в примере 4.3. Из примера 4.3, следует, что комплекс напряжения на источнике пита-ния
1. Определяем активную и реактивную мощности, генерируемые источником питания.
Таким образом, суммарная активная 4. Определяем активную мощность, потребляемую потребителями
Имеет место баланс активных мощностей. 5. Определим реактивную мощность, потребляемую потребителями
Имеет место баланс реактивных мощностей.
Пример 4.8.Составим баланс активных и реактивных мощностей для электрической цепи, представленной на рисунке 4.14 и рассмотренной в примере 4.4. Из примера 4.4, следует, что комплекс напряжения на источнике пита-ния
1. Определяем активную и реактивную мощности, генерируемые источником питания.
Таким образом, суммарная активная 2. Определяем активную мощность, потребляемую потребителями
На резистивных элементах
Суммарная активная мощность
Имеет место баланс активных мощностей. 3. Определим реактивную мощность, потребляемую потребителями На индуктивных элементах
Суммарная реактивная мощность
Имеет место баланс реактивных мощностей.
Поиск по сайту: |

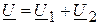 ,
, ,
, 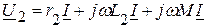 .
.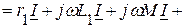

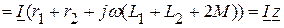 .
.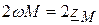 . Это означает, что при наличии индуктивной связи и согласном включении, при одном и том же напряжении
. Это означает, что при наличии индуктивной связи и согласном включении, при одном и том же напряжении 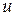 , ток
, ток 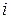 в цепи уменьшается.
в цепи уменьшается.
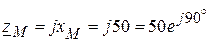 Ом.
Ом.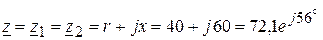 Ом.
Ом.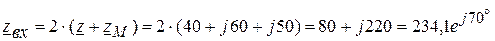 Ом.
Ом.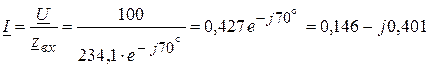 A
A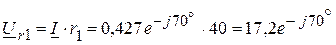 В,
В,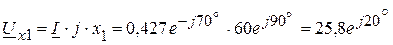 В,
В,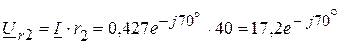 В,
В,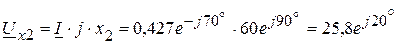 В,
В, В.
В.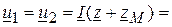
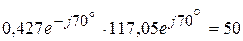 В.
В.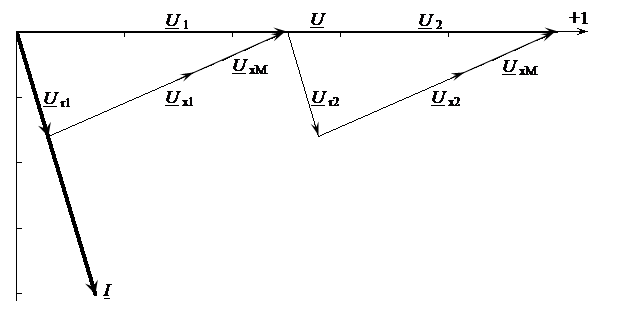
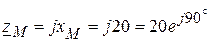 Ом.
Ом.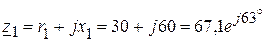 Ом,
Ом,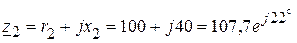 Ом.
Ом.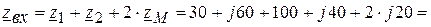
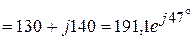 Ом.
Ом.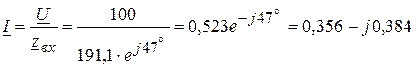 A
A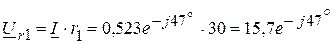 В,
В,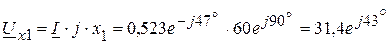 В,
В,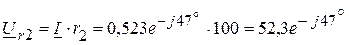 В,
В, В,
В, В.
В.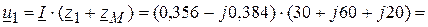
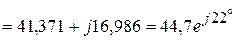 В,
В,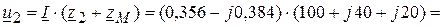
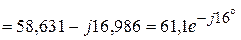 В.
В.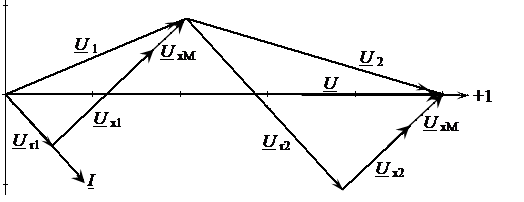
 Рассмотрим встречное включение индуктивно связанных катушек (рис. 4.14).
Рассмотрим встречное включение индуктивно связанных катушек (рис. 4.14). ,
,  .
.
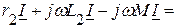
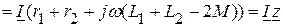 ,
, .
.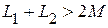 . Это означает, что при наличии индуктивной связи и встречном включении, что при одном и том же напряжении
. Это означает, что при наличии индуктивной связи и встречном включении, что при одном и том же напряжении 
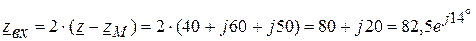 Ом.
Ом.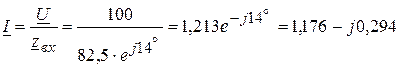 A.
A.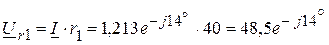 В,
В,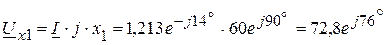 В,
В,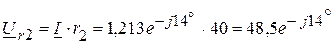 В,
В, В,
В,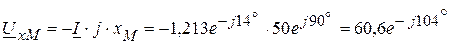 В.
В.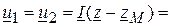
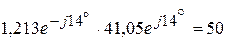 В.
В.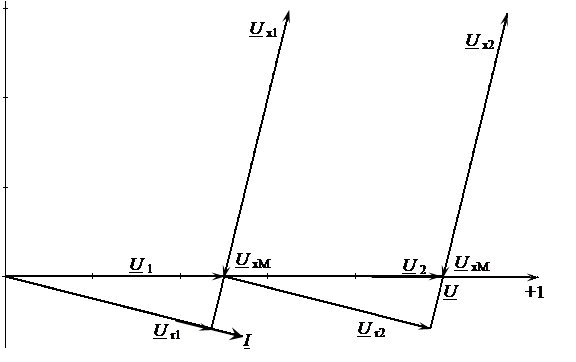

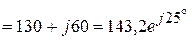 Ом.
Ом.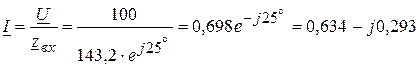 A
A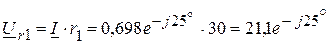 В,
В,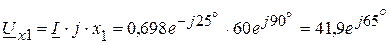 В,
В,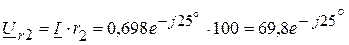 В,
В,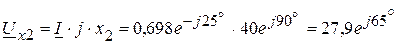 В,
В,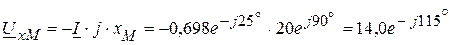 В.
В.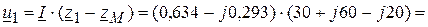
 В,
В,
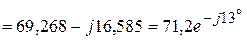 В.
В.
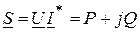 .
.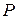 в общем случае
в общем случае 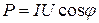 и в соответствии с балансом мощности равна
и в соответствии с балансом мощности равна 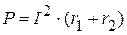 .
.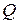 , потребляемая из сети, идет на создание результирующего магнитного поля. При отсутствии индуктивных связей она идет на создание магнитного поля первой и второй катушек и соответственно равна
, потребляемая из сети, идет на создание результирующего магнитного поля. При отсутствии индуктивных связей она идет на создание магнитного поля первой и второй катушек и соответственно равна 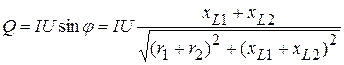 и баланс мощности соответственно равен
и баланс мощности соответственно равен 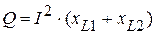 .
. , поэтому из сети будет потребляться большая реактивная мощность
, поэтому из сети будет потребляться большая реактивная мощность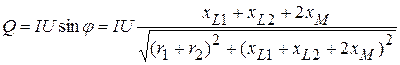 .
.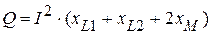 ,
,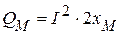 - реактивная мощность, идущая на создание потока взаимной индукции.
- реактивная мощность, идущая на создание потока взаимной индукции.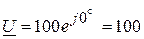 В, а комплекс тока в ветви
В, а комплекс тока в ветви  A.
A.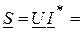
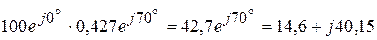 ВА.
ВА.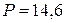 Вт,
Вт, 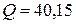 ВАр.
ВАр.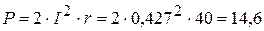 Вт,
Вт,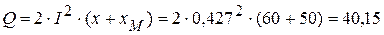 ВАр.
ВАр.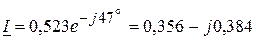 A.
A. ВА.
ВА. Вт,
Вт, 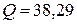 ВАр.
ВАр.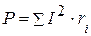 .
. Вт,
Вт,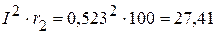 Вт.
Вт.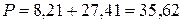 Вт.
Вт. ВАр,
ВАр, ВАр,
ВАр,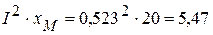 ВАр.
ВАр.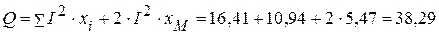 ВАр.
ВАр.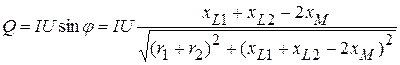 .
.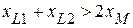 .
. .
.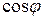 , при согласном включении уменьшается по сравнению с
, при согласном включении уменьшается по сравнению с 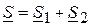 , где
, где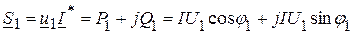 ВА,
ВА,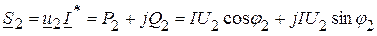 ВА.
ВА.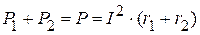 .
.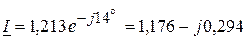 A.
A.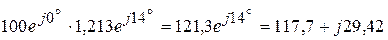 ВА.
ВА.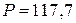 Вт,
Вт, 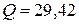 ВАр.
ВАр.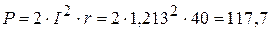 Вт,
Вт,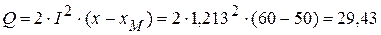 ВАр.
ВАр.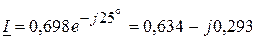 A.
A.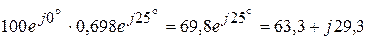 ВА.
ВА.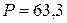 Вт,
Вт, 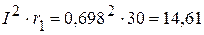 Вт,
Вт,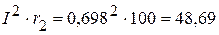 Вт.
Вт.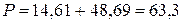 Вт.
Вт.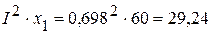 ВАр,
ВАр, ВАр,
ВАр, ВАр.
ВАр. ВАр.
ВАр.