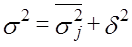|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ПОКАЗАТЕЛИ ВАРИАЦИИ ПРИЗНАКА
Средняя величина дает обобщающую характеристику всей совокупности изучаемого явления. Однако две совокупности, имеющие одинаковую среднюю арифметическую величину, могут значительно отличаться друг от друга по степени колеблемости (вариации) величины изучаемого признака. Если индивидуальные значения признака ряда мало отличаются друг от друга, то средняя арифметическая будет достаточно показательной характеристикой данной совокупности. Если же совокупность характеризуется значительным рассеиванием индивидуальных значений признака, то средняя арифметическая будет ненадежной характеристикой этой совокупности и ее практическое применение будет ограничено. Для познания сущности изучаемой совокупности необходимо исследование индивидуальных различий в значениях какого-либо признака у единиц данной совокупности в один и тот же период или момент времени, т.е. вариации признака. Измерение вариации, выяснение ее причины, выявление влияния отдельных факторов дает важную информацию для принятия научно-обоснованных управленческих решений. Основным инструментом анализа вариации является построение рядов распределения. Ряды распределения представляют собой простейшую группировку, в которой каждая выделенная группа характеризуется одним показателем. Статистическим рядом распределения называется упорядоченное распределение единиц совокупности на группы по определенному изменяющемуся признаку. Под атрибутивным рядом понимается ряд распределения по атрибутивному (качественному) признаку, не имеющему количественной меры. Под вариационным рядом понимается ряд распределения по количественному признаку. Вариационные ряды могут быть дискретными и интервальными. Дискретный ряд распределения - это ряд, в котором варианты выражены целым числом. Интервальный ряд распределения - это ряд, в котором значения признака заданы в виде интервала. В составе вариационного ряда выделяют следующие элементы, варианты, частоты, частости. Варианты – это значения варьирующего признака. Частоты – число единиц совокупности, обладающих данными значениями варьирующего признака. Частости – удельные веса (доли) отдельных групп в общей численности совокупности. Анализ рядов распределения наглядно можно проводить на основе их графического изображения. Для этой цели строят полигон, гистограмму, огиву и кумуляту распределения. Полигон используется при изображении дискретных вариационных рядов. Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака Гистограмма применяется для изображения интервального вариационного ряда. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенным на соответствующих интервалах. Высота столбиков должна быть пропорциональна частотам. В результате мы получим график, на котором ряд распределения изображен в виде смежных друг с другом столбиков. Гистограмма может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединить прямыми. При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах. Это необходимо сделать для устранения влияния величины интервала на распределение частот и получения возможности сравнивать частоты. Плотность распределения - это частота, рассчитанная на единицу ширины интервала, то есть, сколько единиц в каждой группе приходится на единицу величины интервала. Для графического изображения вариационных рядов может использоваться кумулятивная кривая. При помощи кумуляты (кривой сумм) изображается ряд накопленных частот. Накопленные частоты определяются путем последовательного суммирования частот по группам. Накопленные частоты показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение. При построении кумуляты интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломаную линию, то есть кумуляту. Если при графическом изображении вариационного ряда в виде кумуляты оси поменять местами, то получимогиву. Для измерения вариации признака применяются различные абсолютные и относительные показатели. К абсолютным показателям вариации относятся размах колебаний, среднее линейное отклонение, дисперсия, среднее квадратическое (стандартное) отклонение. Размах колебаний, илиразмах вариации, представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности:
Размах вариации зависит от величины только крайних значений признака, поэтому область его применения ограничена достаточно однородными совокупностями. Он применяется в предупредительном контроле качества продукции. Точнее характеризует вариацию признака показатели, основанные на учете колеблемости всех значений признака. Средняя арифметическая является обобщающей характеристикой свойств совокупности. Поэтому большинство показателей вариации основано на рассмотрении отклонений значений признака отдельных единиц совокупности от этой величины. К таким показателям относятся среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю, поэтому для расчета среднего линейного отклонения суммируются абсолютные значения индивидуальных отклонений значений признака. Среднее линейное отклонение для несгруппированных данных для сгруппированных данных Дисперсия для несгруппированных данных для сгруппированных данных Формулы для расчета дисперсии можно привести к виду:
т.е. дисперсия равна разности средней из квадратов значений признака и квадрата средней арифметической.
Дисперсия обладает рядом свойств, некоторые из них позволяют упростить ее вычисления: 1) дисперсия постоянной величины равна нулю; 2) если все варианты значений признака уменьшить на одно и то же число 3) если все варианты значений признака уменьшить в одно и то же число раз ( 4) Дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной:
Среднее квадратическое отклонениепредставляет собой корень квадратный из дисперсии: для несгруппированных данных для вариационного ряда Размах вариации, среднее линейное и среднее квадратическое отклонения являются величинами именованными. Они имеют те же единицы измерения, что и индивидуальные значения признака. Среднее линейное и среднее квадратическое отклонения показывают на сколько в среднем колеблется величина признака у единиц исследуемой совокупности. При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической пользуются относительными показателями вариации. Наиболее часто применяется коэффициент вариации, который измеряет колеблемость в относительном выражении, относительно среднего уровня:
Его используют не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному). Если статистическая совокупность разбита на группы по какому-либо признаку, то для оценки влияния различных факторов, определяющих колеблемость индивидуальных значений результативного признака, можно воспользоваться разложением дисперсии на составляющие: на межгрупповую и внутригрупповую дисперсии. Общая дисперсия Пусть изучаемая совокупность разбита на группы по интересующему нас факторному признаку. Необходимо изучить раздельно вариацию признака внутри однородных в отношении данного фактора групп и изменения в величине признака от группы к группе. Выполнение такой группировки позволяет разложить общую дисперсию признака на две дисперсии, одна из которых будет характеризовать часть вариации, обусловленную влиянием фактора, положенного в основу группировки, а вторая - вариацию, происходящую под влиянием прочих факторов (кроме фактора, положенного в основу группировки). Индивидуальные значения результативного признака обозначим через
Вариацию, обусловленную влиянием фактора, положенного в основу группировки, характеризуетмежгрупповая дисперсия
где Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группевнутригрупповая дисперсия,
где По совокупности в целом вариация значений признака под влиянием прочих факторов характеризуется средней из внутригрупповых дисперсий:
Между общей дисперсией
Пример 5.
Поиск по сайту: |
 , а по оси ординат наносится шкала для выражения величины частот
, а по оси ординат наносится шкала для выражения величины частот  . Частота
. Частота 
 вычисляется по следующим формулам:
вычисляется по следующим формулам:
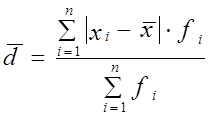
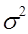 - средняя из квадратов отклонений вариантов значений признака от их средней величины. Дисперсия рассчитывается по следующим формулам:
- средняя из квадратов отклонений вариантов значений признака от их средней величины. Дисперсия рассчитывается по следующим формулам:



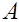 , то дисперсия не изменится;
, то дисперсия не изменится; раз), то дисперсия уменьшится в
раз), то дисперсия уменьшится в 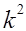 раз;
раз;
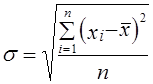


 (дисперсия признака по всей изучаемой совокупности) характеризует вариацию признака как результат влияния всех факторов, определяющих индивидуальные различия единиц совокупности.
(дисперсия признака по всей изучаемой совокупности) характеризует вариацию признака как результат влияния всех факторов, определяющих индивидуальные различия единиц совокупности. . Общая дисперсия результативного признака может быть рассчитана, например, по формуле:
. Общая дисперсия результативного признака может быть рассчитана, например, по формуле:
 , которая является мерой колеблемости групповых средних
, которая является мерой колеблемости групповых средних  , вокруг общей средней
, вокруг общей средней 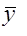 и исчисляется по формуле:
и исчисляется по формуле: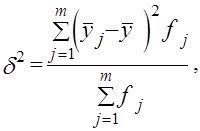
 - число групп;
- число групп; 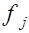 - число единиц в
- число единиц в  группе;
группе;  - частная средняя по
- частная средняя по 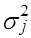 .
.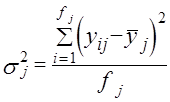
 те элементы из общей совокупности, которые в результате группировки оказались в
те элементы из общей совокупности, которые в результате группировки оказались в 
 и межгрупповой
и межгрупповой