 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Тема 3. СРЕДНИЕ ВЕЛИЧИНЫ и показатели вариацииСтр 1 из 3Следующая ⇒
Средняя величина - обобщающая характеристика изучаемого признака в исследуемой совокупности. Она отражает его типичный уровень в расчете на единицу совокупности в конкретных условиях места и времени, игнорируя различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются и выявляются наиболее типичный уровень признака. Все явления статистической совокупности однокачественны – обладают единой материальной сущностью. В результате явления имеют определенную тенденцию к сходству, которая при расчете средних доводится до логического конца, до отыскания такого уровня признака, который имел бы место при полной тождественности единиц совокупности. Вычисление средней не является простой счетной операцией. Для научно обоснованного использования средних необходимо соблюдать следующие условия: 1. Средние величины должны рассчитываться только по качественно однородным совокупностям. Только при выполнении этого условия средняя как обобщающая характеристика отражает общее, типичное, закономерное, присущее всем единицам исследуемой совокупности. Средние, полученные для неоднородных совокупностей будут описательными, будут искажать характер изучаемого явления. В таких случаях метод средних используется в сочетании с методом группировок, позволяющим выделить однородные группы, по которым и исчисляются типические групповые средние. 2. Средняя должна исчисляться по совокупности, состоящей из достаточно большого числа единиц. Только в этом случае обеспечивается взаимопогашение случайных индивидуальных особенностей, что способствует проявлению основного, существенного, типичного, присущего всей массе единиц. 3. Каждая средняя характеризует изучаемую совокупность лишь по какому-либо одному признаку. Для того, чтобы дать всестороннюю характеристику совокупности, чтобы понять сущность средней, необходимо использовать систему взаимосвязанных средних величин. 4. Средняя должна вычисляться исходя: а) из социально-экономического смысла признака, подлежащего осреднению; с тем, что по существу представляет собой данный признак, соотношениям и каких величин он определяется (логическая форма средней); б) из характера исходных статистических данных, по которым определяется средняя. Формула средней выводится для каждого конкретного случая и форма средней не может быть произвольной. В зависимости от характера исходных данных может быть несколько различных случаев решения, но в любом случае сохранится одна и та же логическая форма этой средней величины. В каждом конкретном случае для реализации логической формы средней требуется одна из форм средней величины: 1) средняя арифметическая; 2) средняя гармоническая; 3) средняя геометрическая; 4) средняя квадратическая. Итак, при выборе вида средней величины обычно исходят из логической сущности осредняемого признака и его взаимосвязи с итоговым показателем. Общий вид степенной средней имеет вид:
Если отдельные значения признака встречаются несколько раз, тогда частота повторения индивидуальных значений признака (вес) присутствует в расчетных формулах степенных средних. В этом случае общий вид степенной средней имеет вид:
Запишем формулы различных видов степенных средних, придавая k значения: -1,0,1,2,. При k = -1 получим среднюю гармоническую величину:
При k = 0 получим среднюю геометрическую величину:
(При этом степень корня совпадает с суммарной степенью отдельных значений признака). При k=1 получим среднюю арифметическую:
При k=2 получим среднюю квадратическую величину:
Степенные средние разных видов, исчисленные по одной и той же совокупности, имеют различные количественные значения. Чем больше показатель степени k, тем больше величина соответствующей средней. Рассмотрим применение различных видов средних величин на примере.
Пример 1. Используя данные, определить средние по каждому признаку. Формулы записать, используя буквенные обозначения признаков. Указать, какие виды средних величин применялись.
При выборе вида средней исходим из экономического смысла показателей. Найдем среднее значение планового задания по выпуску продукции на одну фабрику. Для этого необходимо суммарный объем планового задания всех фабрик разделить на число фабрик
(средняя арифметическая простая). Найдем среднее значение процента выполнения плана на одну фабрику. Для этого необходимо суммарный фактический объем выпуска продукции трех фабрик разделить суммарный объем выпуска трех фабрик по плану и результат умножить на 100%. Фактический объем выпуска каждой фабрики равен произведению планового объема и процента выполнения плана (выраженного в коэффициентах), то есть
или 101,81 % (средняя арифметическая взвешенная)
Определим средний процент (с) стандартной продукции. Для этого необходимо фактически выпущенную стандартную продукцию трех фабрик разделить на фактически выпущенную продукцию трех фабрик и результат умножить на 100%. В результате получим:
(средняя арифметическая взвешенная) Определим средний процент (d) продукции первого сорта. Для этого необходимо фактически выпущенную продукцию первого сорта трех фабрик разделить на фактически выпущенную продукцию трех фабрик и результат умножить на 100%. (Здесь считаем, что дан процент продукции первого сорта из количества выпущенной продукции.) В результате получим:
или 67,85% (средняя арифметическая взвешенная) Определим средние по трем фабрикам затраты (e) на один рубль произведенной продукции. Для этого общие затраты трех фабрик на производство всей продукции разделить всю фактически выпущенную продукцию трех фабрик. В результате получим:
Пример 2 Имеются следующие данные о стоимости и использовании фондов на предприятиях отрасли за 2 смежных квартала:
Определить средний уровень фондоотдачи в 1 и отдельно 2 кварталах. Формулу записать, используя буквенные обозначения. Указать вид средней величины. Решение: 1 квартал. а) логическая формула средней. В соответствии с экономическим содержанием:
б) по условию задачи в 1 квартале у нас известна фондоотдача и объем основных производственных фондов, отсюда определим объем произведенной продукции, т.е. соотношение будет иметь вид:
г) обобщим данные по совокупности заводов и запишем формулу используя буквенные обозначения:
О – осредняемый признак; Ф – признак вес. Средняя арифметическая взвешенная. 2 квартал. Логическая формула средней фондоотдачи та же самая, т.е.
Однако во 2 квартале нам известна фондоотдача и объем произведенной продукции, отсюда определим стоимости основных производственных фондов и соотношение будет иметь вид
Среднюю фондоотдачу необходимо рассчитывать в этом случае по следующему алгоритму:
Вывод: Логическая формула средней одного и того же показателя (соотношением каких величин определяется этот показатель) всегда одна и та же. Однако, в зависимости от исходных данных применяются различные формы средних величин. Свойства средней арифметической. Отдельные значения признака будем называть вариантами. 1. Средняя арифметическая постоянной равна самой постоянной. 2. Если уменьшить (увеличить) все варианты на какое-либо произвольное постоянное число А, то новая средняя уменьшится на то же число.
3. Если уменьшить (увеличить) все варианты в одинаковое число раз k, то средняя уменьшится (увеличится) во столько же раз.
4. Если уменьшить или увеличить веса (частоты)
Частостями
Тогда формула средней арифметической примет вид
Расчет средней арифметической взвешенной по сгруппированным данным В этом случае за значения признака принимаются середины интервалов. Пример 3. Имеются следующие данные о распределении заводов цементной промышленности по величине производственной мощности:
Часто первый и последний интервал являются открытыми. При расчете средней величины считают, что величина таких интервалов равна величине соседних с ними интервалов.
Поиск по сайту: |



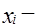 варианты значений признака, индивидуальные значения осредняемого признака;
варианты значений признака, индивидуальные значения осредняемого признака; частота повторения данного варианта, признак вес.
частота повторения данного варианта, признак вес. (средняя гармоническая простая)
(средняя гармоническая простая) (средняя гармоническая взвешенная)
(средняя гармоническая взвешенная) (средняя геометрическая простая)
(средняя геометрическая простая) (средняя геометрическая взвешенная)
(средняя геометрическая взвешенная) (средняя арифметическая простая)
(средняя арифметическая простая)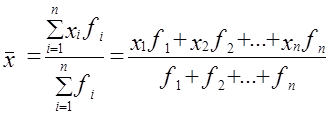 (средняя арифметическая взвешенная)
(средняя арифметическая взвешенная)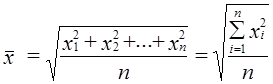 (средняя квадратическая простая)
(средняя квадратическая простая) (средняя квадратическая взвешенная).
(средняя квадратическая взвешенная).
 . Тогда среднее значение процента выполнения плана равно
. Тогда среднее значение процента выполнения плана равно
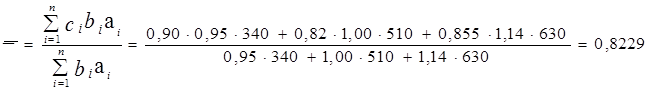 или 82,29%
или 82,29%

 Объем ОПФ
Объем ОПФ

 - средняя гармоническая взвешенная.
- средняя гармоническая взвешенная.


 всех вариантов в какое-либо постоянное число раз, то средняя арифметическая не изменится.
всех вариантов в какое-либо постоянное число раз, то средняя арифметическая не изменится.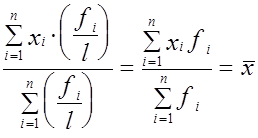
 (относительными частотами) называются отношения частот к общему числу наблюдений, то есть к сумме всех частот:
(относительными частотами) называются отношения частот к общему числу наблюдений, то есть к сумме всех частот:

