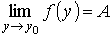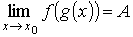|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Односторонний предел по Коши ⇐ ПредыдущаяСтр 2 из 2
Свойства.
Теоремы. Пусть числовые функции f (x) и g (x) определены на некотором интервале, быть может, кроме точки х0 этого интервала, и имеют конечные пределы в этой точке
Тогда
Предел алгебраической суммы конечного числа функций, имеющих в данной точке конечный предел, равен алгебраической сумме пределов этих функций в этой же точке:
Предел произведения конечного числа функций равен произведению пределов этих функций, при условии, что последние существуют.
Предел отношения двух функций равен отношению пределов этих функций, при условии, что последние существуют и предел знаменателя не равен нулю.
Предел отношения двух функций, имеющих предел в данной точке, равен отношению пределов этих функций в той же точке, если предел знаменателя отличен от нуля:
то
Предел промежуточной функции. Если в некоторой окрестности точки х0 выполняется неравенство g (x) < f (x) < p (x) и
то
Предел суперпозиции двух функций. ( Пусть функции g: (a, b) → (c, d) и f : (c, d) \ { y0} → Z и имеют пределы
Тогда
Предельный переход в неравенстве.
тогда справедливо неравенство А ≤ B.
Поиск по сайту: |
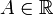 называется правосторонним пределом (правым пределом, пределом справа) функции
называется правосторонним пределом (правым пределом, пределом справа) функции 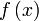 в точке
в точке 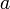 , если для всякого положительного числа
, если для всякого положительного числа  отыщется отвечающее ему положительное число
отыщется отвечающее ему положительное число 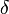 такое, что для всех точек
такое, что для всех точек 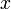 из интервала
из интервала 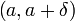 справедливо неравенство
справедливо неравенство  .
. 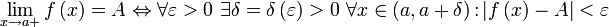
 справедливо неравенство
справедливо неравенство 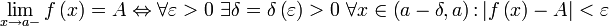
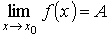 и
и 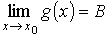
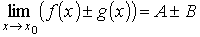
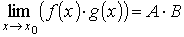
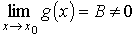 ,
,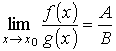
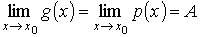
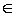 (а, b) радиуса δ в выколотую окрестность точки y0
(а, b) радиуса δ в выколотую окрестность точки y0 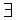 Δ > 0 ) (
Δ > 0 ) (  0 < | x - x0 | < Δ ) : | g ( x ) – y0 | > 0.
0 < | x - x0 | < Δ ) : | g ( x ) – y0 | > 0.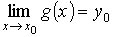 и
и