 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Расчёт балки из обычного железобетона ⇐ ПредыдущаяСтр 3 из 3
Расчёт на прочность по изгибающему моменту. Расчёту подлежат балочные пролётные строения железнодорожных мостов из обычного железобетона ( типовой проект серии 3.501-108). Действительную форму поперечного сечения приводим к расчётной форме (рис. 5).
Рис. 5. Расчётная схема поперечного сечения главной балки.
Вычисляем приведённую (среднюю) толщину плиты при фактической ширине плиты bf=2,09 м:
hf’= Максимальная ширина плиты сжатой зоны тавровых и коробчатых сечений, учитываемая в расчёте, ограничена длиной свесов плиты, которая не должна быть больше 6hf=1,56 м ; расчётная ширина плиты bf’ таврового сечения не должна превышать значения bf’ Действительная форма плиты переменной толщины и вутов заменяется в расчётном сечении прямоугольной формой с толщиной hf’ и шириной bf’. Центр тяжести арматуры ориентировочно назначается на расстоянии as=0,16 м от нижней грани пояса балки. Расчёт на прочность по изгибающему моменту производим, начиная с наиболее нагруженного сечения. Определим в первом приближении высоту сжатой зоны бетона x1 при действии расчётного момента М2=11318,71 кН/м: x1=h0- Получаем x1=0,3241 м >hf’=0,26 м , то из этого следует, что в сжатую зону, кроме плиты входит часть ребра главной балки, и сечение рассчитывается как тавровое. Расчетный изгибающий момент М2 можно представить как сумму двух моментов: М2`- воспринимаемый свесами плиты, М2`` - воспринимаемый сжатой зоной ребра.
М2= М2`+ М2``
Предельный момент, воспринимаемый свесами плит
М2`=
По оставшейся части момента
М2``= М2- М2`=11318,71-7112,55=4206,16 кН
Находим высоту сжатой зоны в ребре:
x1=h0-
Плечо пары внутренних сил таврового сечения z=
Определяем необходимая площадь рабочей арматуры
Армирование будем производить пучками арматурой класса А-III диаметром d=40мм. Площадь поперечного сечения одного стержня равна 8,04 см2. Определяем необходимое количество стержней: nст Принимаем количество стержней nст=27.
После уточнения площади As c учётом принятого количества стержней арматуры находим значение x2: x2= Окончательное значение z вычисляем по формуле:
z=
Условие прочности сечения по изгибающему моменту записывается в виде Мпр=RsAsz³М2 Мпр=330000*339,39*10-4*1,0333=11573,05 кН³ М2=11318,71 кН. Проверка выполняется, расчёт сечения на прочность по изгибающему моменту закончен.
Расчёт на трещиностойкость по касательным напряжениям. Расчёт по касательным напряжениям выполняем в предположении упругой работы конструкции, но без учёта бетона растянутой зоны. В расчёте ограничивается величина касательных напряжений, действующих по нейтральной оси сечения. Касательные напряжения могут быть определены по формуле:
где b - толщина ребра балки; z - плечо пары внутренних сил из расчёта на прочность по изгибающему моменту. При переменной толщине ребра балки из условия
Максимальная поперечная сила, воспринимаемая при меньшей толщине ребра b2:
Расстояние от места изменения толщины до середины пролёта будет равно
Рис. 6. Схема к расчёту на трещиностойкость по касательным напряжениям. Расчёт на прочность по поперечной силе.
Поперечная сила в наклонном сечении воспринимается отогнутой арматурой, хомутами и бетоном сжатой зоны. Места отгибов стержней рабочей арматуры согласуем с эпюрой действующих в балке изгибающих моментов. Предельный момент, воспринимаемый сечением с одним стержнем рабочей арматуры равен
Рис.7. Схема к расчёту главной балки.
Угол наклона стержней к оси балки α=45˚. Не менее 1/3 стержней рабочей арматуры доводим без отгибов до опоры ( см. рис.7). Проверка прочности наклонного сечения (рис.8.) на действие поперечной силы производится из условия:
где Q - максимальное значение поперечной силы от внешних нагрузок; Rsw=0,8Rs - расчётное сопротивление арматуры отогнутых стержней и хомутов; Asi и Asw - площади поперечного сечения соответственно одного отогнутого стержня и всех ветвей хомута, пересекающего наклонное сечение;
с - длина горизонтальной проекции сечения.
Проверка наклонного сечения у опоры. На приопорных участках длиной 2h0 наклонное сечение составляет с продольной осью балки угол 45˚, длина его горизонтальной проекции равна с=h0-x=1,24-0,11=1,13 м. Располагая схемой размещения отогнутых стержней ( рис.8), определяем количество стержней, пересекающих наклонное сечение и их суммарную площадь Площадь всех ветвей одного хомута определяется из выражения:
где dsw - диаметр хомутов; n - число ветвей одного хомута.
Шаг хомутов на концевых участках принимаем asw=10см, в середине пролёта - asw=15см.
Рис. 8. Схема к расчёту наклонного сечения у опоры.
Производим проверку:
Проверка наклонного сечения в середине пролёта. В середине пролёта прочность наклонного сечения обеспечивается постановкой хомутов с шагом 15 см. Длина проекции наклонного сечения равна 2h0=2,48 м. Количество хомутов, пересекающих наклонное сечение, равно 16. Проводим проверку наклонного сечения:
Список использованной литературы:
Поиск по сайту: |


 =
=  =0,26 м.
=0,26 м. b+12hf’=3,62 м, а длина свесов плиты между соседними балками не должна быть больше 0,5(B-b)=0,5(1,80-0,50)=0,65 м, где B=1,80 м- расстояние между осями главных балок.
b+12hf’=3,62 м, а длина свесов плиты между соседними балками не должна быть больше 0,5(B-b)=0,5(1,80-0,50)=0,65 м, где B=1,80 м- расстояние между осями главных балок. =1,24-
=1,24-  =0,3241 м.
=0,3241 м. и соответствующей частью рабочей арматуры, равен:
и соответствующей частью рабочей арматуры, равен:
 =15,5*1000*(2,09-0,5)*0,26*(1,24-0,5*0,26)=7112,55 кН
=15,5*1000*(2,09-0,5)*0,26*(1,24-0,5*0,26)=7112,55 кН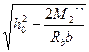 =1,24-
=1,24-  =0,5676 м.
=0,5676 м. =
=  =1,047 м.
=1,047 м. .
. =
=  =26,06 шт.
=26,06 шт. =
=  =0,6184 м.
=0,6184 м.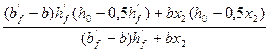 =
=  =1,0333 м.
=1,0333 м.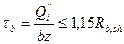 ;
;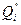 - поперечная сила в рассматриваемом сечении;
- поперечная сила в рассматриваемом сечении; определяем толщины b1 и b2 в опорном сечении и в середине пролёта:
определяем толщины b1 и b2 в опорном сечении и в середине пролёта: .
. =0,5693 м=56,93см; принимаем b1=57 см;
=0,5693 м=56,93см; принимаем b1=57 см; =0,4014 м=40,14 см; принимаем b2=41 см.
=0,4014 м=40,14 см; принимаем b2=41 см. =1465,80 кН.
=1465,80 кН.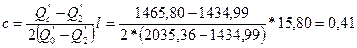 м.
м.
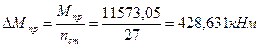 .
.
 ;
; - поперечное усилие, передаваемое на бетон сжатой зоны сечения;
- поперечное усилие, передаваемое на бетон сжатой зоны сечения; .
. =2,26 см2;
=2,26 см2;
 ;
; , проверка выполняется, прочность приопорного участка обеспечена!
, проверка выполняется, прочность приопорного участка обеспечена! , проверка выполняется, прочность сечения в середине пролёта обеспечена!
, проверка выполняется, прочность сечения в середине пролёта обеспечена!