 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Елементи математичної статистики ⇐ ПредыдущаяСтр 2 из 2
Статистичним розподілом вибірки називають перелік варіант варіаційного ряду
Для досліджень вибірку, яка містить більше 10 варіант, розбивають на інтервали. Кількість інтервалів підраховують за формулою:
Довжина інтервалів дорівнює:
Значення на інтервалі приймають як середнє значення інтервалу. Емпіричною функцією розподілу називають функцію
Точковою називають статистичну оцінку, що визначається одним числом. Незміщеною називають точкову оцінку, математичне очікування якої дорівнює оцінюваному параметру при будь-якому обсязі вибірки. Зміщеною називають точкову оцінку, математичне очікування якої не дорівнює оцінюваному параметру. Вибірковою середньою
Вибірковою дисперсією називається середнє арифметичне квадратів відхилень значень від вибіркової середньої:
де
Виправлене середнє квадратичне відхилення розраховується за формулою:
Інтервальною називають оцінку, що визначається двома числами - кінцями інтервалу, що покриває оцінюваний параметр. Довірчим називають інтервал, що із заданою надійністю Інтервальнаоцінкаматематичного сподівання розраховується за формулою::
де
2. Приклади розв′зання типових задач Приклад 1 У конверті знаходяться 20 пронумерованих карток. Навмання дістають дві з них. Знайти ймовірність того, що їх номери 11 і 3. Розв′язання: Уведемо позначення: подія
Приклад 2 Зроблено залп із двох гармат. Імовірність влучення в мішень із першої гармаи дорівнює б) ціль не уражена. Розв′язання: а) Уведемо позначення: подія
б) Уведемо позначення: подія
Приклад 3 Два мисливці одночасно стріляють по меті. Імовірність влучення в мету Ι-м мисливцем Розв′язання: Уведемо позначення: подія
За формулами (1.1.6, 1.1.7) розраховуємо
Приклад 4 Прилад складається з 5-ти вузлів. Ймовірність вийти з ладу для будь якого вузла однакова Розв′язання: Уведемо позначення: подія
Приклад 5 Знайти найімовірнішу кількість ясних днів у вересні, якщо за даними багаторічних спостережень відомо, що у вересні в середньому буває 11 непогожих днів. Розв′язання: Задача вирішується за формулою ( ), де кількість днів у вересні
Приклад 6 Було посаджено 400 дерев. Знайти ймовірність того, що число дерев, що прижилися, більше 350. якщо ймовірність . що окреме дерево приживеться 0,8. Розв′язання: За умовами задачі маємо
Поиск по сайту: |
 (спостережні значення
(спостережні значення  (сума всіх частот дорівнює об’єму вибірки
(сума всіх частот дорівнює об’єму вибірки  ).
).


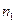






 (1.3.1)
(1.3.1) (1.3.2)
(1.3.2) , визначаючу для кожного значення
, визначаючу для кожного значення 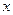 відносну частоту події
відносну частоту події  :
: (1.3.3)
(1.3.3)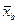 називається середнє арифметичне значень ознаки вибіркової сукупності
називається середнє арифметичне значень ознаки вибіркової сукупності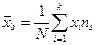 (1.3.4)
(1.3.4) (1.3.5)
(1.3.5) - середнє арифметичне квадратів значень вибірки.
- середнє арифметичне квадратів значень вибірки.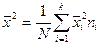 (1.3.6)
(1.3.6) (1.3.7)
(1.3.7) покриває оцінюваний параметр.
покриває оцінюваний параметр. ; (1.3.8)
; (1.3.8)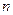 - обсяг вибірки;
- обсяг вибірки; - точність оцінки;
- точність оцінки; - значення аргументу функції Лапласа, для якого
- значення аргументу функції Лапласа, для якого  .
. - поява карток з номерами 11 и 3 одночасно. Шукана ймовірність
- поява карток з номерами 11 и 3 одночасно. Шукана ймовірність  визначаеться за формулою (1.1.1).
визначаеться за формулою (1.1.1).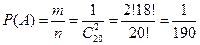 ;
; - число елементарних подій, які сприяють події
- число елементарних подій, які сприяють події 
 , кількість способів, якими можна з 20 елементів витягти по 2 елемента.
, кількість способів, якими можна з 20 елементів витягти по 2 елемента. , із другої -
, із другої -  . Знайти ймовірності наступних подій: а) ціль уражена тільки однією гарматою;
. Знайти ймовірності наступних подій: а) ціль уражена тільки однією гарматою; або другою, тоді перша не влучила - подія
або другою, тоді перша не влучила - подія  . Використовуючи формули (1.1.2, 1.1.5) маємо:
. Використовуючи формули (1.1.2, 1.1.5) маємо: ,
, 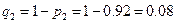 ;
; .
.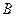 - ціль не уражена, тобто і перша і друга гармати не влучили вціль. Використовуючи формулу (1.1.5) розраховуємо:
- ціль не уражена, тобто і перша і друга гармати не влучили вціль. Використовуючи формулу (1.1.5) розраховуємо: .
. , ΙΙ -м -
, ΙΙ -м -  . У результаті в мету влучає тільки один мисливець. Знайти ймовірність того, що промахнувся Ι-й мисливець.
. У результаті в мету влучає тільки один мисливець. Знайти ймовірність того, що промахнувся Ι-й мисливець. - Ι-й мисливець промахнувся;
- Ι-й мисливець промахнувся; - Ι-й мисливець влучів у ціль.
- Ι-й мисливець влучів у ціль. :
: ;
;  ;
; ;
;  ;
;

 . Знайти ймовірність безвідмовної роботи приладу, якщо для цього потрібно, щоб працювало не менше 4-х вузлів.
. Знайти ймовірність безвідмовної роботи приладу, якщо для цього потрібно, щоб працювало не менше 4-х вузлів. ;
; 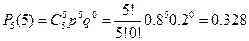
 .
. , ймовірність появи ясного дня
, ймовірність появи ясного дня  , ймовірність появи хмарного дня
, ймовірність появи хмарного дня  .
. ;
; ;
;  .
. ,
,  ,
,  ,
,  ,
, 