 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Армирование напрягаемой арматурой
Для предварительного натяжения монолитных пролетных строений канатах - 60 - 110 мм, при 19 канатах - 96- 110 мм. Расположение пучков напрягаемой арматуры по длине пролета зависит от способа производства работ. Ниже на рис.3.12 и 3.13 приведены схему расположения арматуры при бетонировании на перемещаемых подмостях и при навесном бетонировании.
Рис. 3.12. Схема продольного армирования напрягаемой арматурой при бетонировании на перемещаемых подмостях
Рис.3.13. Схема продольного армирования напрягаемой арматурой при навесном бетонировании
№11 Соединение и анкеровка пучков. Напрягаемые элементы допускается стыковать специальными узлами, называемые куплерами. Отечественное стыковочное устройство УАСО-19 для стыкования пучков из 19 канатов выполнено в виде единой круглой опорной плиты (рис.3.14), в средней части которой имеются конусные отверстия под трехдольные клинья для закрепления первого из пучков, а по стыкуемых внешнему контуру выточены продольные прорези, в которые, после натяжения первого пучка, устанавливают канаты второго пучка с обжимными анкерами на концах. На весь узел надевается защитный металлический кожух, к которому присоединяется каналообразователь
Рис.3.14. Конструкция отечественного куплера УАСО-19 для стыкования пучков из 19 канатов. Концевые анкера имеют аналогичную структуру. Кроме того, в качестве концевых анкеров применяются устройства типа фонарика, схема которого приведена на рис.3.15.
Рис.3.15. Конструкция концевого анкера типа «фонарик». Этот тип анкера изготавливают путем предварительного раскручивания и осаживания конца каната на длине -200 мм. При осаживании проволоки в пластической стадии расходятся на диаметр 100 мм. При такой анкеровке зона передачи усилия на бетон равна 840 мм.
№12 1) Опорные части стаканного типа(рис.4.1) Опорная часть состоит из стальных круглых в плане опорной плиты 1 и обоймы 2, в которой находится слой резины 3.
Рис.4.1.Элементы опорной части стаканного вида
Поперечные деформации резины полностью исключаются, что позволяет поднять её сопротивление до 1000 кгс/см2. Резиновая прокладка, заключенная в стальную обойму, ведет себя при больших давлениях как вязкая жидкость и допускает поворот в любом направлении как сферический шарнир. Стаканные опорные части обеспечивают только угловые деформации, поэтому могут быть использованы в качестве неподвижных опорных частей. Применяются в неразрезных пролетных строениях во всем возможном диапазоне пролетов, так как несущая их способность легко изменяется за счет изменения диаметра стальной обоймы. 2) Комбинированные опорные части(рис.4.2) Включают в себя стаканную опорную часть для обеспечения угловых перемещений и элемент скольжения для обеспечения линейных перемещений.
РИС.4.2.Элементы Комбинированной опорной части: 1-пролетное строение;2-стальная крышка; 3- резиновая уплотняющая прокладка; 4 - опора; 5 -полированный лист из нержавеющей стали; 6- стальная обойма; 7- резиновая прокладка: 8- стальная опорная плита: 9-фторопласт.
Состоит из нескольких элементов: стальной крышки, резиновой уплотняющей прокладки, полированного листа из нержавеющей стали, стаканной опорной части и фторопласта в кольцевых выточках стальной обоймы. Для обеспечения угловых перемещений может включать стальной балансир. Отечественные предприятия освоили производство нижеприведенных опорных частей для неразрезных пролетных строений (рис.4.3 и 4.4)
Рис.4.3. Линейно подвижная стаканная опорная часть СОЧ- ЛП 1. - стакан; 2-скользящая плита; 3 -фторопластовый диск; 4 - крышка; 5- резиновый вкладыш; 6 -уплотнительные кольца; 7 - ушки для транспортировки; 8 - транспортные болты; 9- футляр; 10 -прокладная плита; 11 - пластмассовые болты; 15 - пара трения: фторопласт- полированная сталь
Рис.4.4. Конструкция шаровой сферической линейно- подвижной опорной части (ШСОЧ —ЛП):1- нижний балансир;2 - верхний балансир( шаровой сегмент); 3-скользящая плита; 4 - фторопластовый диск; 5 - ушки для транспортировки; 6 - транспортный болт; 9 - футляр; 10 — указатель перемещений; 11 -пара трения; 12 -направляющая; 14-прокладная плита; 15 - слезник; 16 -болты крепления нижнего балансира к плите.
Опорные части располагаются обычно на подферменнике, представляющем собой выступ на опоре в виде параллелепипеда, монолитно связанного с опорой и армированного сетками ненапрягаемой арматуры. Сетки усиливают прочность бетона при местном воздействии не него больших опорных реакций. Подферменники имеют ровную поверхность для размещения опорной части, передают опорную реакцию на опору. В плане их размеры должны превышать размеры опорной части в любом направлении не менее чем на 15 см, выступающие части должны иметь уклоны.
№13 Конструкция закрытого деформационного шва (рис.5.1).
Рис. 5.1. Элементы закрытого деформационного шва: 1-покрытие; 2- армирующая сетка; 3- защитный слой; 4- гидроизоляция; 5-отделяющая прокладка; 6-перекрытие зазора; 7- компенсатор; 8 -анкерный стержень; 9- мастика; 10 - пористый заполнитель.
Шов создается в следующем порядке: 1 .В выравнивающий слой бетона в зоне шва укладывается компенсатор 7 из оцинкованной стали с анкерным стержнем 8 из круглой стали. 2.По всей верхней поверхности компенсатора укладывается гидроизоляция 4. 3.Полость в изогнутой части компенсатора заполняется упругим пористым заполнителем. 4.Над гидроизоляцией укладывается защитный слой 3 бетона. Над пористым заполнителем - мастика 9. 5.Осуществляется перекрытие 6 зазора над швом и укладка отделяющей прокладки 5 на длине 70- 80 см.Она обеспечивает распределение полного перемежения на этой длине без трещинообразования в асфальтобетоне. 6.Устраивается двухслойное асфальтобетонное покрытие 1, армированное над швом арматурной сеткой 2 Максимальная амплитуда допускаемых перемещений в швах закрытого типа в случае применения неармированного асфальтобетона составляет 10 мм, в случае армированного 15 мм .
Конструкция заполненных деформационных швов(рис. 5.2 и 5.3).
К швам заполненного типа относят конструкции с заполнением мастикой (рис. 5.2) или с резиновыми вкладышами-компенсаторами (рис. 5.3). В заполненных деформационных швах покрытие устраивают с зазором, который впоследствии заполняют упругим материалом (см. рис. 5.2). Его деформации обеспечивают перемещения торцов пролетных строений.
Рис.5.2.Деформационные швы с заполнением мастикой: а- при асфальтобетонном покрытии; б- при цементобетонном покрытии с устройством бетонного прилива; в — варианты усиления кромки шва стальным окаймлением
Надежность работы этих швов зависит от материала заполнения и прочности кромок. При увеличении зазора создаются условия для разрушения кромок цементобетонных покрытий. В связи с этим кромки усиливают (рис. 5.2, в) стальными окаймлениями с надежной их анкеровкой. Перемещения, допускаемые на швы с заполнением мастиками, составляют при асфальтобетонном покрытии 12 мм, при цементобетонном—18 мм, при цементобетонном с окаймлением— 22 мм. Деформационные швы с резиновыми компенсаторами (рис. 5.3, а) применяют при перемещениях до 30 мм в мостах и путепроводах I—V категорий и в городах. На дорогах I категории и в городах допускается устройство модульных швов с двумя рядами компенсаторов, обеспечивающих перемещения до 100 мм (рис. 5.3, б).
Рис. 5.3.Конструкции деформационных швов с резиновыми компенсаторами: а-с одним компенсатором К-8; б- с двумя компенсаторами К-8.
Деформационные швы с резиновыми компенсаторами применяют в районах с минимальной среднесуточной температурой воздуха выше температуры хрупкости резины (+5°С).
№14 В перекрытых швах горизонтальные перемещения торцов пролетных
Рис. 5.4. Деформационные швы перекрытого типа: а—с плоским скользящим листом; б — со скошенным скользящим листом; в — со скошенным «плавающим» скользящим листом; 1—скользящий лист; 2—резиновая прокладка;3 — пружина; 4 — окаймление кромки; 5 — ребро жесткости окаймления; 6 — водоотводный лоток
Деформационный шов с плоским скользящим листом (см. рис. 5.4, а) состоит из окаймления 4 с ребрами жесткости 5 и хомутами, омоноличенного в незабетонированных участках плиты проезжей части, скользящего листа 1, опирающегося на резиновые прокладки 2 и прижатого пружиной 3, и водоотводного лотка б. Скользящий лист на подвижном конце имеет скос для выдавливания грязи из зазора. Пружины размещены в обойме, заполненной техническим вазелином. Деформационные швы со скошенным скользящим листом (рис. 5.4, б) и с плавающим листом (рис. 5.4, в) обеспечивают более плавный въезд автомобилей на шов и перемещения до 300 мм. Еще более плавный проезд по швам обеспечивают швы с гребенчатыми плитами (см. рис. 5.5), но предельное перемещение, обеспечиваемое ими, составляет 250 мм.
Рис. 5.5. Деформационные швы с гребенчатыми плитами: а- консольного типа; б-скользящего типа.
При перемещениях более 300 мм применяют более сложные конструкции швов откатного типа.
№15 назначение и конструкция сопряжения моста с насыпью Деформационные швы являются дорогостоящими и сложными элементами мостового полотна. В связи с этим наметилась тенденция к сокращению их числа путем применения неразрезных и температурно-неразрезных пролетных строений, обеспечивающих лучшую плавность движения транспортных средств. В неразрезных мостах существует минимальное количество деформационных швов. Их устанавливают только между торцами пролетных строений и шкафными стенками устоев. Эти швы обеспечивают плавность въезда и съезда на мост и способствуют сопряжению моста с насыпью подходов. 4. Сопряжение моста с насыпью Одним из наиболее важных требований к сопряжению моста с насыпью является обеспечение плавности перехода от насыпи к мосту. Этому способствует устройство одинакового покрытия на мосту и подходах. Кроме того, необходимо обеспечить плавность перехода от различных упругих деформаций насыпи и пролетного строения как по величине деформаций, так и по скорости их протекания. Это достигается путем создания в местах сопряжения моста с насыпью специальных переходных участков в виде переходных плит, отмосток и подушек из щебенчатых и песчано-гравийных материалов (рис. 5.6).
Рис. 5.6. Сопряжение моста с подходами с помощью переходной плиты
Переходные плиты одним концом опираются на выступ шкафной стенки, а другим — на железобетонный лежень. Плиты укладывают с уклоном 1 : 10 в сторону насыпи и закрепляют штырями. Под плитой устраивают подушку из дренирующего материала.
№16 А) массивные Б) на оболочках и буровых столбах В) свайные опоры Факторы: Грунты, ледоход, условия в которых производится строительство
№18 Область применения и конструкция промежуточных опор на оболочках и буровых столбах. Защита их от ледохода.
При нормальных грунтовых условиях и наличии у строителей соответствующих механизмов опоры мостов выполняют без фундаментов в виде нескольких столбов, объединенных поверху железобетонными ригелями. Для неразрезных пролетных строений с пролетами 42 и более метров применяются промежуточные опоры на оболочках или буровых столбах. На рис. 6.5. приведена конструкция промежуточной опоры при пролетах 63- 84 м на реках с сильным ледоходом.
Рис.6.5.Конструкция промежуточной опоры моста с приподнятым над меженью ростверком: 1- отметка после первого размыва; 2- граница подводного бетона; 3- грунтовая пробка; 4-монолитный бетона; 5- металлические накладки. Основание этой опоры выполнено из восьми свай - оболочек диаметром 160 см, погруженных в грунт на глубину 18. 4 м от отметки возможного местного размыва. Нижняя часть оболочки на высоте 3 м заполнена грунтом 3. а верхняя часть заполнена бетоном 2 и на длине 1,4 м входит в ростверк. Ростверк опоры представляет собой приподнятую над уровнем межени монолитную железобетонную плиту, облицованную специальными плитами и блоками защиты от ледохода из бетона класса прочности В4 и марку по морозостойкости F 400. Блоки защиты установлены в верхней части ростверка и имеют скосы по всему периметру. Плиты и блоки защиты ростверка объединены в единую конструкцию специальными металлическими закладными деталями на сварке и при объединении с оболочками монолитным бетоном класса В 22,5 выполняли функцию опалубки. Тело опоры выполнено из двух металлических стоек диаметром 1.42 м, заполненных арматурой и бетоном и объединенных монолитным железобетонным ригелем. При пролетах 21-42 м и высоте опор до 8 м применяются безростверковые опоры на железобетонных оболочках или буронабивных столбах (рис.6.6).
Рис.6.6 .Конструкция безростверковой опоры на оболочках или буровых столбах: 1- блок ригеля; 2- блок верхней части столба опоры; 3- блок фундаментной части опоры.
Количество оболочек в опоре зависит от величины пролета и габарита моста. Диаметр оболочек обычно 60, 120 и 160 см. Опоры такого типа составляются из блоков ригеля, блоков верхней части столбов и фундаментной их части. Фундаментная часть столбов в обычном грунте может быть выполнена из вибропогружаемой сваи-оболочки диаметром 120 см. длиной 14, 16, 18, 20, 22 и 24 м. В нижней части оболочки над грунтовым ядром устраивается бетонная пробка из литого бетона методом подводного бетонирования, над ней оболочка заполняется песком до переменного уровня воды, заполнение полости оболочки в зоне переменного горизонта воды осуществляется бетоном. При скальных грунтах фундаментная часть столбов из оболочек погружается до скального грунта вибропогружателем, а в дальнейшем заделывается в грунт в соответствии с рис.6.7.
Рис.6.7. Узел заделки фундаментной части оболочки в скальный грунт
На рис.6.8. приведена конструкция узла объединения блоков верхней и фундаментной части столбов- оболочек.
Рис.6.8. Конструкция узла объединения блоков верхней и фундаментной Части столбов- оболочек: 1-верхняя часть столба; 2- бетон омоноличивания; 3- бетон усиления фундаментной части в узле объединения ; 4- оболочка фундаментной части столба.
№19 Область применения и конструкция монолитных и сборно-монолитных промежуточных опор. Защита их от ледохода.
Монолитные опоры мостов применяют при реализации нестандартных решений. Им можно придавать любые архитектурные формы в соответствии с ландшафтом местности или архитектурой окружающих строений. Их применяют также в районах, удаленных от заводов сборного железобетона. На рис.6.1. приведены различные конструкции монолитных промежуточных опор. На реках с сильным ледоходом опоры возводят с ледорезами (рис.6.1,а), ледорезы значительно увеличивают объем тела опор и фундаментов и значительно удорожают строительство. Во многих случаях возможна замена объемных ледорезов верховыми ребрами с водорезами (рис.6.1,б).
Рис.6.1. Промежуточные монолитные опоры мостов: а- с ледорезом; б- с водорезом; в- массивная с раздельными столбами выше уровня высоких вод; г-массивная с раздельными столбами, тонкой перемычкой между ними и ригелем.
Размеры этих опор чаще всего назначают по конструктивным и архитектурным соображениям, прочность бетона в них полностью не используется. С целью экономии материала тело опоры выполняют меньших размеров с двухконсольными железобетонными оголовками (рис.6.1,б) , устанавливают столбы выше уровня высоких вод (рис.6.1,в) или столбы с тонкими перемычками между ними и ригелем(рис.6.1,г). Столбчатые опоры без ригелей (рис.6.1,в) целесообразно применять для многопролетных мостов с двумя главными балками. Такие опоры позволяют свободно перемещать вдоль моста специальные смотровые тележки, что облегчает осмотр и ремонт элементов пролетных строений. На рис. 6.2. в качестве примера приведена конструкция монолитной опоры с железобетонным двухконсольным ригелем.
Рис. 6.2. Конструкция монолитной опоры с железобетонным двухконсольным ригелем
Стремление удешевить возведение массивных опор за счет сокращения или полного отказа от опалубки привело к разработке сборно-монолитных конструкций опор, у которых контур выполнен из сборных элементов, а внутренний объем заполнен монолитным бетоном или бутобетоном. На рис. 6.3. приведена конструкция сборно-монолитной опоры с контурными блоками. До уровня высоких вод тело опоры выполнено из контурных блоков, заполненных бутобетоном. На массивную часть опоры уложена сборная плита толщиной 50 см из двух монтажных элементов. На плиту установлены столбы из оболочек, на верху которых выполнены монолитные железобетонные прямоугольные капители. Ригель из двух монтажных элементов таврового сечения опирается на капители через резиновые опорные части, что обеспечивает четкость статической работы ригеля как свободно лежащей балки. Блоки ригеля омоноличены по продольному шву, армированному петлями из стержней арматуры, выпущенных из полок блоков. С целью обеспечения возможности монтажа сборно-монолитных опор кранами грузоподъемностью 7- 10 т контурные блоки могут быть малых размеров с массой 5-7 т. На рис. 6.4 приведена сборно-монолитная опора с контурными блоками сложной конфигурации. Перевязка швов достигается за счет применения блоков разной ширины. Арматурные выпуски из блоков позволяют надежно анкеровать их в монолитной кладке.
Рис. 6.3. Сборно-монолитная опора с контурными блоками
Рис.6.4.Сборно-монолитная опора с контурными блоками небольшой массы и сложной конфигурации.
№20 Пролетные строения (рис.1) со сплошным (или с небольшими пустотами) поперечным сечением, отношение ширины которого к высоте не превышает 7 - 8, а размеры поперечного сечения значительно меньше длины пролета. С расчетной точки зрения такие пролетные строения можно рассматривать как массивные упругие брусья. Под воздействием внешних нагрузок они изгибаются и закручиваются без изменения контура поперечного сечения. Для этой группы пролетных строений возможна расчетная модель в виде системы массивных упругих брусьев (рис.16), когда несколько таких брусьев жестко объединяются между собой.
Рис.1.Пролетные строения, работающие как массивные упругие брусья. Расчет этих пролетных строений и их систем производится обычно на основе классической теории стержневых систем:
на изгиб в одной плоскости с использованием дифференциального уравнения(1),
(1)
где W- упругий прогиб в плоскости изменения кривизны; М-изгибающий момент, ЕI-жесткость бруса при изгибе;
а кручение с использованием уравнением (2).
где θ- угол закручивания, Т- крутящий момент, GIt— жесткость бруса при кручении.
Уравнения (1) и (2) позволяют определить внутренние силовые факторы от изгиба и кручения, по которым находятся соответствующие напряжения. Конструкцию сложной разветвленной эстакады можно представить в виде системы упругих криволинейных брусьев, моделирующей пролетное строение.
№21 Пролетные строения (рис.2) со сплошным (или с небольшими пустотами) поперечным сечением, отношение ширины которого к высоте больше 7-8, а размеры ширины сечения значительно меньше длины пролета. Под воздействием внешних нагрузок такие пролетные строения изгибаются и закручиваются с искривлением контура поперечного сечения. Для этой группы пролетных строений возможна расчетная модель в виде упругих плит.
Рис.2. Пролетное строение в виде упругой плиты.
Расчет этих пролетных строений можно выполнять методами теории упругости как изотропной пластинки, если считать, что изгибная жесткость плиты в продольном и поперечном направлениях одинакова. При заданной функции нагрузки q(х,у) решение задачи расчета плиты в этом случае заключается в получении функции прогибов w(х,у), удовлетворяющей граничным условиям и дифференциальному уравнению (3) изгиба изотропной пластинки
где х, у — координатные оси; q- внешняя распределенная нагрузка; D -цилиндрическая жесткость, являющаяся постоянной величиной и определяемая по формуле
где Е, μ- модуль упругости и коэффициент Пуассона материала пролетного строения; h- толщина плитного пролетного строения.
Дифференциальное уравнение (3) решается с учетом граничных условий по кромкам плиты. Для однопролетной плиты (рис. 3а) по пролетным кромкам прогибы W, изгибающие моменты Мх и углы поворота
Рис.3.Схемы к расчету плитных пролетных строений как упругих пластинок.
В многопролетных строениях к граничным условиям необходимо добавлять условия совместности деформаций в над опорных сечениях (рис. 3б) ( изгибающие моменты и поперечные силы равны по величине и противоположны по знаку). Определение функции w(x,y), удовлетворяющей уравнению (3) и граничным условиям, представляет собой сложную математическую задачу. (Обычно используется метод Фурье). При найденной функции w(x,y) необходимые расчетные силовые факторы в любой точке плиты определяются известными соотношениями теории упругости
где -Мх My Mxy _ изгибающие моменты на единицу длины сечения: QX; Qy - поперечные силы на единицу длины сечения.
Плитное пролетное строение обычно имеет различную изгибную жесткость дифференциальное уравнение изгиба ортотропной пластинки следующего вида
№22 Диафрагменные ребристые или коробчатые пролетные строения с недеформируемым контуром поперечного сечения, составленного из тонкостенных стержней.
Тонкостенным называют стержень, составленный из пластинок, отношение высоты или ширины которых к их толщине не менее 7-8, а длина стержня значительно превышает контуры поперечного сечения. При работе такого пролетного строения под воздействием нагрузок контуры его поперечного сечения не деформируются благодаря наличию диафрагм по его длине. Особенностью этих пролетных строений является то, что в их поперечных сечениях возникают напряжения не только от изгиба и свободного кручения, но и от стесненного кручения, создающегося вследствие наличия диафрагм.
Рис4 Пролетные строения с тонкостенным недеформируемым контуром поперечного сечения.
Изгиб этих пролетных строений рассчитывается с помощью уравнения (1). Для расчета кручения таких ребристых пролетных строений, которые являются тонкостенными стержнями с открытым контуром поперечного сечения, используется теория В.З.Власова, дающая следующее дифференциальное уравнение стесненного кручения (5)
m(x) -интенсивность внешней закручивающей нагрузки.
Для расчета кручения тонкостенных стержней с замкнутым контуром поперечного сечения используется теория тонкостенных стержней замкнутого профиля, разработанная А.А. Уманским. Основное дифференциальное уравнение (6), полученное им из условий равновесия, отличается от уравнения В.З.Власова дополнительным членом в правой части
отличающаяся от соответствующей характеристики в уравнении В.З.Власова коэффициентом депланации μ;
секториальный момент инерции сечения.
Решение уравнений (5) и (6) находится в виде суммы общего решения однородного уравнения, получаемого при равенстве нулю правой части, и частного решения, учитывающего действие внешней нагрузки, соответствующей правой части. При решении однородного уравнения используется метод начальных параметров, в качестве которых принимается: начальный угол закручивания и мера депланации сечения, бимомент и полный крутящий момент, соответствующие сечению на конце пролетного строения. Значения этих параметров зависят от характера опирания и закрепления концов пролетного строения. При этом в каждом поперечном сечении находят, помимо угла закручивания, также бимомент Вw,изгибно-крутящий момент Мw и момент свободного кручения Mt .Этим внутренним усилиям соответствуют нормальные σи касательные τнапряжения свободного и стесненного σw , τ w τt кручения.
При этом должны быть вычислены дополнительные геометрические характеристики сечения: Iw-главный секториальный момент инерции сечения; Sw-главный секториальный статический момент инерции сечения.
Определение нормальных и касательных напряжений от изгиба производится на основе технической теории изгиба.
№23 Бездиафрагменные коробчатые пролетные строения с замкнутым деформируемым поперечным сечением (рис.5).
Помимо изгиба, свободного и стесненного кручения поперечные сечения испытывают деформации контура.
Рис.5. Пролетное строение с тонкостенным деформируемым контуром поперечного сечения
Расчет этих пролетных строений на кручение производится в два этапа. На первом этапе определяются усилия в соответствии с теорией тонкостенных стержней с замкнутым недеформируемым контуром, а на втором этапе учитывают влияние деформаций контура по нижеприведенной схеме.(рис.б)
Рис.6.Схемы к расчету сечений коробчатых балок.
T=Mi+Mw R1+R2=Ri+Rj M1+M2=Mi+Mj
В соответствии с этой схемой напряженное состояние поперечного сечения пролетного строения с заданной нагрузкой Р (рис. а) представляется в виде суммы напряженных состояний того же сечения с симметричным (рис. б) и кососимметричным (рис. в) воздействием. При этом сечение по схеме б) будет работать только на изгиб, а сечение по схеме в) только на кручение. Далее на первом уровне симметрично загруженная балка рассматривается с не деформируемым контуром поперечного сечения (рис г). При этом определяются изгибающие моменты Mz и поперечные силы Qy., воспринимаемые полным сечением балки, а по ним напряжения σх и τху. На втором уровне учитывают местный поперечный изгиб элементов сечения от внеузлового приложения нагрузки при несмещающихся узлах контура. Для замкнутой поперечной рамы задача может быть решена методом сил с лишними неизвестными Х1 и Х2 в середине нижней плиты рамы (рис. д) с получением нормальных σх и касательных τyz напряжений в верхней плите, а также напряжений σу в стенках балки.
Для несимметрично загруженной балки можно рассмотреть три уровня
При таком подходе от действия полного внешнего крутящего момента Т=Mi+Mw в сечениях коробчатой балки возникают внутренние бимоменты Вw и соответствующие им нормальные напряжения стесненного кручения σw, моменты свободного кручения Мi вызывающие касательные напряжения τi и изгибно-крутящие моменты Мw с касательными напряжениями от стесненного кручения τw. При этом должны быть вычислены дополнительные геометрические характеристики сечения: Iw – главный секториальный момент инерции сечения; Sw- главный секториальный статический момент инерции сечения. Тогда в общем случае загружения балки осевой силой с изгибом и кручением полное выражение для нормальных и касательных напряжений будет иметь следующий вид
где ω - главная секториальная координата точки, в которой вычисляется напряжение.
№24 Пролетные строения, представляющие собой сочетание балок и плит- цилиндрические складчатые оболочки. К ним относятся бездиафрагменные ребристые и многокоробчатые пролетные строения соединенные плитой проезжей части.(рис.7)
Рис.7. Деформации поперечных сечений пролетных строений в виде цилиндрических складчатых оболочек.
Для расчета пролетных строений этой группы требуется использовать наиболее сложные методы расчета. Наибольшее применение нашел метод плитно-балочных конструкций, разработанный Улицким Б.Е. с учениками. В соответствии с этим методом пролетное строение расчленяют продольными разрезами на отдельные плиты и балки (стенки). В отличие от плоских систем, характеризуемых тем, что одно из измерений — длина — имеет величину большего порядка, чем два остальных, пролетные строения мостов являются пространственными конструкциями, в которых два измерения — длина и ширина — могут быть одного порядка. В общем случае напряженное состояние в сечении пространственной конструкции определяется тремя компонентами сил и тремя компонентами моментов, а изменение его положения — тремя компонентами линейных и тремя компонентами угловых перемещений. Расчет пространственных конструкций мостов имеет много общего с расчетом плоских статически неопределимых систем. Он включает в -себя следующие этапы: выбор основной системы и назначение лишних неизвестных; установление физико-механических констант материалов и вычисление геометрических характеристик сечений; вычисление коэффициентов канонических уравнений; решение систем уравнений (определение значений неизвестных усилий, перемещений); вычисление ординат поверхностей влияния усилий и деформаций в различных элементах конструкции; определение расчетных величин усилий и деформаций. Отдельные этапы пространственного расчета имеют свои характерные особенности, отличные от расчетов плоских систем. Бездиафрагменные конструкции пролетных строений мостов, состоящие из главных балок и плит в одном и двух уровнях, изображены на рис. /, а, б. В .пространственных расчетах подобные конструкции условно расчленяют продольными сечениями на отдельные элементы — балки, плиты, стержни. В зависимости от стоящих перед расчетчиками задач, сложности и требуемой точности расчета рекомендуется применять следующие схемы членения:
Рис. 1. Схемы членения плитно-балочных пролетных строений а) на тавровые, двутавровые или другого .сечения балки (рис. 1,в, г); б) на балки и горизонтальные плиты (рис. 1, д, е,)\ в) на стержни, вертикальные и горизонтальные плиты (рис. 1,ж, з),
В случаях когда требуется детально рассчитать плиту проезжей части, рекомендуется схема, изображенная на рис. 1, д, е; когда необходимо рассчитать главные балки на кручение и определить возникающие в их стенках поперечные изгибающие моменты — схема, представленная на рис. 1, ж, з; в расчетах сложных конструкций и систем мостов используют схему, изображенную на рис. 1,0, г. В отдельных случаях может оказаться целесообразным применение и других схем членения. Взаимодействие между собой отдельных продольных элементом, их деформации и возникающие4 между ними внутренние усилия можно определить исходя из положений метода сил, метода перемещений или смешанного метода. Как и в строительной механике плоских систем, выбор того или иного метода зависит от конкретных задач, стоящих перед расчетчиком. Лишние неизвестные в зависимости от их особенностей могут быть выражены в виде функций или дискретных величия. Взаимодействие продольных элементов пролетного строения (главных балок, плит) между собой характеризуется усилиями или перемещениями, которые выражают в виде функций от абсциссы х, направленной вдоль пролета. Взаимодействие продольных п поперечных элементов пролетного строения, например главных балок и диафрагм, характеризуется дискретными величинами усилий и моментов. В пространственных расчетах одновременно учитывают продольные, поперечные (горизонтальные и вертикальные) и крутильные перемещения конструкции .пролетного строения. В связи с этим для принятой схемы членения необходимо вычислить следующие геометрические характеристики: для сечений балок и стержней — «приведенные» площади, моменты инерции при изгибе относительно горизонтальной и вертикальной нейтральных осей, моменты инерции при кручении, положение центров тяжести и изгиба, секториальные характеристики (для балок); для плит — цилиндрические жесткости. В методе сил лишними неизвестными являются силы и моменты в сечениях между смежными элементами. На единице длины сечения учитывают четыре компонента сил и моментов (рис. 2, а), В методе перемещений в конструкцию условно вводят дополнительные связи, а неизвестными являются компоненты перемещений (рис. 2, б). В плоскостях разрезов вводят неизвестные непрерывно изменяющиеся вдоль координаты х нормальные N(x), поперечные Q(x), сдвигающие усилия Т(х), а также изгибающие моменты М(х). Характер изменения неизвестных вдоль разрезов зависит от внешней нагрузки и характеристик пролетного cтроения.
Рис.2. Компоненты : а) усилий: б) перемещений.
Эти силы и моменты являются функциями абсциссы x, направленной вдоль пролета и принимающей на его концах значения 0 и L. Их выражают в форме тригонометрических рядов:
Все внешние нагрузки также представляют в тригонометрических рядах с использованием известных формул для коэффициентов разложения различных нагрузок в ряд Фурье.
Для определения неизвестных составляют канонические уравнения метода сил, характеризующие условия совместности деформаций плит и балок. В общем виде для каждого продольного сечения составляется четыре уравнения, характеризующие : 1. совместность продольных перемещений U вдоль оси х; 2. совместность поперечных перемещений V вдоль оси у; 3. совместность поперечных перемещений W вдоль оси z; 4. совместность поворотов Ф относительно продольной оси х.
В этих уравнениях учитываются суммарные перемещения (линейные V, U, W и угловые Ф) от воздействия всех неизвестных N, Т, Q, М и внешней нагрузки q. Уравнения (В) составляют для каждого разреза, причем деформации плитных элементов определяют методами теории упругости как для пластинок, а деформации балочных элементов методами сопротивления материалов как для упругих брусьев. При решении системы (В) линейных уравнений определяют постоянные коэффициенты an,bn>Cn>dn для всех сечений, после чего по формулам (А) находятся соответствующие величины усилий. Зная величины внутренних и внешних усилий, приложенных к каждому элементу, можно вычислить деформации и напряжения, действующие в каждом из них. Метод плитно-балочных конструкций отличается высокой точностью получаемых результатов, однако требует проведения громоздких вычислений и применяется только в сочетании с ПК. К недостаткам метода можно отнести также сложность учета переменности сечений по длине пролетов и граничных условий в сложных системах Для расчета пролетных строений группы 5 в последнее время широкое применение находит метод конечных элементов. Эффективность метода связан"а с возможностью наиболее просто учитывать различные краевые условия, особенности прикладываемых нагрузок, форму рассчитываемых конструкций и т. д. При этом конструкции расчленяется на некоторое число элементов конечных размеров, деформированное состояние которых является простым. Дискретизация конструкций пролетных строений должна при этом быть произведена таким образом, чтобы соблюдалось равенство энергий заданной системы и ее заменяющей модели. В зависимости от требуемой точности расчета и особенностей рассчитываемой конструкции применяются три типа аппроксимации заданной системы, а именно: стержневая, двухмерными и трехмерными конечными элементами. Связь между конечными элементами предполагается только в узловых точках, перемещения которых принимаются за основные неизвестные. Напряженно-деформированное состояние каждого конечного элемента однозначно определяется через его узловые перемещения и реактивные усилия взаимодействия между элементами. Переход от узловых перемещений к перемещениям точек внутри конечных элементов осуществляется с помощью аппроксимирующих функций, задаваемых априорно. Основное требование, предъявленное к этим функциям, состоит в возможности обеспечения неразрывности перемещений при переходе от одного конечного элемента к другому. Для аппроксимации перемещений внутри конечных элементов обычно используют степенные полиномы.
№25 Основная идея и средство приближенного определения усилий в балках с учетом пространственной работы пролетного строения. Временная нагрузка на ездовом полотне пролетного строения автодорожного моста может располагаться в продольном и в поперечном направлении по отношению к оси моста самыми разными способами. Извсех возможных её положений необходимо в процессе расчета установить самое невыгодное с учетом пространственной работы сооружения. Наиболее строго эта задача решается с использованием поверхности влияния нагрузки на тот или иной силовой фактор, действующий в расчетном сечении балки. Поверхности влияния в настоящее время представляется возможным получать с помощью компьютеров, но в рамках курсового проектирования в МАДИ такой возможности пока нет из -за отсутствия компьютерного класса у кафедры мостов. Поэтому будем вычислять силовые факторы приближенно с помощью коэффициента поперечной установки. Основной идеей этого расчета является выделение доли временной нагрузки, приходящейся на рассматриваемый несущий элемент пролетного строения. Эта доля при ручных расчетах выделяется с помощью коэффициента поперечной установки. Он вычисляется при нагружении поперечной линии влияния нагрузки на рассматриваемую балку, которая является по существу поперечным сечением поверхности влияния.
Поиск по сайту: |
























 (2)
(2)
 (3)
(3)
 в направлении оси х равны нулю, а по боковым граням Qy=Му= Мху= О
в направлении оси х равны нулю, а по боковым граням Qy=Му= Мху= О

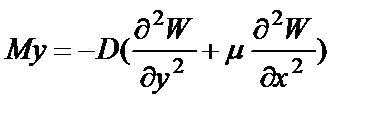



 (4)
(4)



 (5)
(5) -изгибно-крутильная характеристика сечения, зависящая от модулей сдвига Gи упругости Е,момента инерции на кручение Itи секториального момента инерции сечения Iw;
-изгибно-крутильная характеристика сечения, зависящая от модулей сдвига Gи упругости Е,момента инерции на кручение Itи секториального момента инерции сечения Iw; (б)
(б) -изгибно-крутильная характеристика сечения,
-изгибно-крутильная характеристика сечения, -коэффициент депланации сечения; 1tмомент инерции
-коэффициент депланации сечения; 1tмомент инерции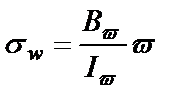








 (A)
(A) (B)
(B)