 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Проектирование элементов катушек индуктивностиСтр 1 из 2Следующая ⇒
ВЫСОКОЧАСТОТНЫЕ КАТУШКИ ИНДУКТИВНОСТИ
Катушки индуктивности – это компоненты РЭС, предназначенные для взаимного преобразования энергии электрического тока в энергию магнитного поля. При этом энергия электрического поля переходит в энергию магнитного поля и наоборот. Катушки индуктивности являются высокочастотными компонентами РЭС и обычно используются в диапазоне частот от 100 кГц до 300 МГц. Вопросы для самопроверки 1. Приведите определение катушки индуктивности, объясните принцип ее действия. Что такое индуктивность? 2. Выполните классификацию высокочастотных катушек индуктивности. 3. Приведите примеры обозначений катушек индуктивности на электрических схемах. 4. Нарисуйте схему замещения катушки индуктивности, перечислите паразитные параметры катушки. Как влияют паразитные параметры на характеристики катушки? 5. Приведите определения основных электрических параметров высокочастотных катушек индуктивности. 6. Объясните сущность поверхностного эффекта и эффекта близости. Почему диаметр провода обмотки влияет на значение добротности катушки? 7. Приведите определение оптимального диаметра провода обмотки высокочастотной катушки. 8. Почему применение намоточного провода “литцендрат” ведет к повышению добротности катушки? 9. Перечислите магнитные материалы, применяемые для изготовления сердечников высокочастотных катушек индуктивности. Сформулируйте требования к параметрам этих материалов. 10. Перечислите типы и конструкции магнитных сердечников для высокочастотных катушек индуктивности. 11. Напишите выражения для расчета относительной магнитной проницаемости mотн различных типов сердечников. 12. Дайте определение тангенса угла магнитных потерь. Почему значение tgdm зависит от частоты электромагнитного поля? 13. Напишите выражения для расчета индуктивности катушек с цилиндрическим, броневым и кольцевым сердечниками. 14. Как влияет на индуктивность и добротность катушки индуктивности электромагнитный экран? Требования к материалам для изготовления электромагнитных экранов. 15. Перечислите типы, объясните конструкции катушек с переменной индуктивностью. В каких радиотехнических устройствах целесообразно применять ферровариометры? 16. Объясните порядок расчета катушки индуктивности с цилиндрическим сердечником. 17. Объясните порядок расчета катушки индуктивности с броневым сердечником. 18. Изменится ли индуктивность катушки на кольцевом сердечнике, склеенном из двух половинок, по сравнению с катушкой, выполненной на целом кольцевом сердечнике, и почему? 19. Из каких конструктивных элементов состоит катушка индуктивности ? Примеры решения задач 4.2.1. Расчет характеристик высокочастотных катушек Пример 4.1. Рассчитать индуктивность L соленоида со следующими параметрами: 1) число витков N=1000; 2)диаметр соленоида Dк =0,8 см; 3) длина соленоида l = 12 см. Решение. 1. Значение индуктивности L является коэффициентом пропорциональности между потокосцеплением Y и величиной переменного тока i, протекающего через соленоид (рис. 4.1): Y = Li, Вб , (4.1) где Y = ФN = BSN – потокосцепление, Вб = Т×м2; Ф – переменный поток магнитной индукции, Вб; B = momH – индукция магнитного поля, Т; mo = 4p×10–7 Г/м – магнитная постоянная; m – магнитная проницаемость среды, в которой находится катушка (в качестве среды служит сердечник катушки); H = l – длина катушки, м; N – число витков катушки; Таким образом, потокосцепление равно Подставляя в выражение (4.1) значение Y,для индуктивности соленоида получаем выражение
Выражение (4.2) справедливо при расчетах индуктивности катушек, намотанных на магнитопроводах с замкнутой магнитной цепью (например, кольцевых или броневых).
2. Для расчета индуктивности соленоида выразим в формуле (4.2) значение площади поперечного сечения соленоида S через диаметр Dк:
Тогда
где все размеры выраженыв см. Подставляя в формулу (4.3) исходные данные задачи, получим:
Ответ. L=526,2 мкГ Пример 4.2. Рассчитать индуктивности Lк высокочастотных катушек, изображенных на рис.4.2, а-в при следующих исходных данных: а) число витков N=6; диаметр Dк =1,2 см; длина намотки l=1,0 см; б) число витков N=4; диаметр Dк =1,2 см; длина намотки l=1,3 см; шаг намотки τ=3 мм; диаметр провода без изоляции d0= 1 мм; в)число витков N=100; диаметр Dср =1,5см; длина намотки l=0,9 см;глубина намотки t=0,3 см.
Решение. Цилиндрические катушки получают методом намотки провода на каркас цилиндрической формы, изготовленный из диэлектрического материала. Обмотки цилиндрических катушек индуктивности имеют небольшую длину l по сравнению с диаметром каркаса Dк (рис. 4.2, а–в) и характеризуются заметным рассеянием магнитного потока, создаваемого током в катушке. Поэтому выражение (4.3) не годится для расчета коротких цилиндрических катушек индуктивности. 1. Для выполнения инженерного расчета индуктивности цилиндрической катушки без сердечника в формулу (4.3), вводится параметр L0, и расчетная формула представляется выражением L = LoN2Dк×10–3, мкГ. (4.4) Для однослойных катушек (рис.4.2, а, б) параметр Lо = f(l/Dк), где l – длина намотки. Для многослойных катушек (рис.4.2, в) Lо = f(l/Dср, t/Dср), где t – глубина намотки катушки, Dср – средний диаметр катушки, см. Графики значений коэффициента Lo для однослойных и многослойных катушек представлены на рис. 4.3 и 4.4. 2. Для однослойной катушки с шагом L = [LoN2Dк – 2πNDк (A+B)] ×10–3, мкГ, (4.5) где A=f(d0/τ) и B=f(N) определяются из рис. 4.5; d0 – диаметр провода без изоляции; τ – шаг намотки. Подставляя в формулы (4.4) и (4.5) значения условий задачи, получим следующие результаты: а) l/Dк=1/1,2=0,83; из графика рис. 4.3 следует, что Lo= 7,7; подставляя в формулу 4.4 получим ,что L = 7,7·62·1,2·10–3 =0,333 мкГ.
б) l/Dк=1,3/1,2=1,083; из графика рис.4.3 следует, что Lo=6,5; d0/τ =1/3=0,3; из графиков рис.4.5 следует, что А(0,3)= – 0,5 и B(4)=0,18; подставляя в формулу 4.5 получим ,что L = [6,5×42×1,2 – 2×3,14×4×1,2 (-0,5+0,18)]×10–3= =[124,8+9,65] ×10–3
в) l/Dср=0,9/1,5=0,6; t/Dср =0,3/1,5=0,2; из графика рис.4.4 следует, что Lo=7,5; подставляя в формулу 4.4 получим, что L = 7,5·(100)2·1,5·10–3 =112,5 мкГ. Ответ: а) L=0,333 мкГ; б) L=0,134 мкГ; в) L=112,5 мкГ Пример 4.3. Рассчитать добротность Q катушки индуктивности при следующих исходных данных: 1) частота f=2,4 МГц; 2) индуктивность L=15 мкГ; 3) обобщенное сопротивление потерь в катушке
Решение. Полная эквивалентная электрическая схема замещения высокочастотной катушки индуктивности изображена на рис. 4.6, а. На этой схеме используются следующие обозначения: L Воспользовавшись упрощенной эквивалентной схемой высокочастотной катушки, изображенной на рис. 4.6, б, выражение для добротности катушки можно записать в виде
где f – частота переменного тока i, протекающего через катушку, Гц; Подставляя исходные данные задачи в выражение (4.6), получим:
Ответ. Q=75,4. Заметим, что максимальное значение добротности высокочастотных катушек индуктивности обычно не превышает 300¼400 ед. Пример 4.4.Рассчитать сопротивление потерь в собственной емкости следующих катушек: а) однослойная катушка с Dк =12 мм и индуктивностью L=50 мкг; тангенс угла диэлектрических потерь изоляции провода и каркаса катушки tgdиз =8·10-3 на частоте f=1,2 МГц ; б) многослойная катушка с Dср =20 мм с индуктивностью L=1,9 мкг; диэлектрическая проницаемость изоляции провода намотки e=4; tgdиз =5·10-3 на частоте f=0,24 МГц Решение. Собственная емкость катушки – это емкость, возникающая между отдельными витками катушки, витками и металлическими частями конструкции РЭС. Собственная емкость катушки ухудшает ее добротность, внося дополнительное сопротивление потерь RCL. При этом активная мощность, выделяющаяся в диэлектрической изоляции обмотки, равна
Отсюда следует формула для расчета последовательного сопротивления потерь RCLв собственной емкости катушки:
Собственную емкость однослойных катушек можно оценить по формуле CL = (0,5…1,5)Dк , пФ, (4.8) где Dк – диаметр каркаса, см. Собственную емкость многослойных катушек рассчитывают из выражения CL = pDср(8,5e + 8,2)10–1, пФ, (4.9) где Dср – средний диаметр намотки, см; e – диэлектрическая проницаемость изоляции провода намотки. 1. Согласно формуле (4.8) собственная емкость однослойной катушки равна CL = 0,5·1,2=0,6 пФ. Подставляя в формулу (4.7) полученное значение CL и исходные данные задачи для однослойной катушки получим следующий результат
2. Согласно формуле (4.9) собственная емкость многослойной катушки равна CL =3,14·2,0(8,5·4+8,2)0,1=26,5 пФ. Подставляя в формулу (4.7) полученное значение CL и исходные данные задачи для однослойной катушки получим следующий результат
Ответ: а) RCL=0,0051 Ом;б) RCL=0,72 Ом. Пример 4.5.Рассчитать сопротивлениепровода катушки индуктивности току высокой частоты при следующих исходных данных: 1) частота f=2,4 МГц; 2) диаметр провода без изоляции d0=0,45 мм; 3) средний диаметр намотки Dср=10 мм; l=8,5 мм; 4) число витков намотки N=15 Решение. Для частот f
где F(z) и G(z) – функции Бесселя от переменной z = 0,106do Графики значений функций F(z) и G(z) представлены на рис. 4.7, а. График значений коэффициента k = f(l/D) изображен на рис. 4.7, б. Сопротивление постоянному току цилиндрической катушки с простой многослойной намоткой из одножильного медного провода равно
где Dcр и do должны быть выражены в мм, а удельное сопротивление r – в Ом×мм. 1. Рассчитываем значения параметров, входящих в формулу (4.10). Из формулы (4.11) получаем значение сопротивления провода намотки постоянному току:
Параметр z рассчитываем из соотношения z = 0,106do Из графиков рис.4.7, а следует, что функция Бесселя F(7,4)
2. Подставляя значения параметров в формулу (4.10), получим что
Ответ. Rм=0,48 Ом; Пример 4.6.Рассчитать сопротивлениепровода цилиндрической катушки индуктивности току высокой частоты, намотанной проводом "литцендрат" при следующих исходных данных: 1) частота f=0,8 МГц; 2) марка провода намотки ЛЭШО 15х0,08; 3) средний диаметр намотки Dср=15 мм; l=8,5 мм; 4) число витков обмотки N=90 Решение. Сопротивление току высокой частоты катушек, намотанных проводом “литцендрат”, на средних частотах в несколько раз ниже сопротивления аналогичных катушек, намотанных эмалированным одножильным проводом с дополнительной шелковой изоляцией, следовательно, добротность таких катушек выше. Сопротивление току высокой частоты катушек, намотанных проводом “литцендрат”, вычисляется по формуле
где Rм – сопротивление, Ом; d – диаметр отдельной жилки, см; n – число жил; do – полный наружный диаметр литцендрата (без учета наружной изоляции), приближенно равный (при малых d)
e = 1,55¼2,0 – коэффициент, зависящий от числа жил. Сопротивление постоянному току катушки, намотанной литцендратом, равняется
В формуле (4.10) величины Dср и d должны быть выражены в мм, а коэффициент а = 1,02¼1,06 учитывает удлинение жилки за счет скрутки. 1. Рассчитываем значения параметров, входящих в формулу (4.12). Из формулы (4.14) получаем значение сопротивления провода намотки постоянному току (коэффициент а=1,04):
2.По формуле (4.13) рассчитываем полный наружный диаметр литцендрата do
3. Параметр z рассчитываем из соотношения z = 0,106do Из графиков рис.4.7, а следует, что функция Бесселя F(4) 2. Подставляя значения параметров в формулу (4.10), где e = 1,77, получим что
Ответ. Rм=2,7 Ом. Пример 4.7.Рассчитать сопротивление провода однослойной катушки метрового диапазона со следующими исходными данными: 1) частота f=60 МГц; 2) диаметр катушки D =8 мм; 3) число витков обмотки N=10; 4) диаметр провода обмотки d0=0,8 мм. Решение. Расчет сопротивления провода однослойных катушек метрового диапазона, применяемых в системах КВ и УКВ радиотелефонной и телевизионной связи (частоты 30¼300 МГц), производится по формуле
где D – диаметр катушки, см; do – диаметр провода без изоляции, см; f – частота в МГц. Подставляя в формулу (4.15) условия задачи, получаем
Ответ. Rм=0,41 Ом. Пример 4.8.Рассчитатьcопротивление потерь Rm в сердечнике катушки, изготовленном из феррита марки 50ВЧ при следующих исходных данных: 1) частота f=20 МГц; 2) индуктивность 1,5 мкГ. Решение. Характеристикой потерь в ферромагнитных сердечниках высокочастотных катушек является тангенс угла магнитных потерь, tgdm. Значение тангенса угла магнитных потерь в общем случае определяется соотношением
где Rm – активное cопротивление потерь в сердечнике, вносимое в общее последовательное сопротивление потерь высокочастотной катушки; wL – реактивное сопротивление катушки. Зависимость tgdm от частоты для некоторых ферритов представлена на рис. 4.6, а и б [1]. 1. Из формулы (4.16) получаем выражение для расчета активного cопротивления потерь в сердечнике: Rμ=2πfL·tgδμ. (4.17) Из графика рис. 4.8, а находим значение tgδμ
Подставляя в формулу (4.17) получаем Rμ=2πfL·tgδμ.=6,28·20·106·1,5·10-6·7·10-3=1,32 Ом. Ответ. Rμ=1,32 Ом. Пример 4.9.Рассчитатьотносительную магнитную проницаемость μотн цилиндрического магнитного сердечника при следующих исходных данных: 1) тип сердечника - СЦР6х10; 2) материал сердечника - феррит 1000НМ3; 3) диаметр катушки Dк=1,3 см; 4) длина катушки lк=0,9 см. Решение. Цилиндрические сердечники (рис. 4.9, а–г) – это сердечники марок СЦР (с резьбой), СЦГ (гладкие), СЦТ (трубчатые).
Сердечники с резьбой используются для подстройки катушек, гладкие – для подстройки катушек и для изготовления магнитных антенн, трубчатые – для подстройки в ферровариометрах. Гладкие и трубчатые сердечники выпускаются только из феррита. В технической документации размеры сердечника обозначаются в виде Относительная магнитная проницаемость цилиндрического сердечника рассчитывается по формуле mотн = mнkmk' , (4.18) где km = f(Dк/Dc) и k' = f(lк/Dc) – коэффициенты, рассчитываемые с помощью графиков на рис. 4.10.
1. Из графика на рис. 4.10, а, б определяем значения коэффициентов kμ(13/6)= kμ(2,15) 2. Подставляя исходные данные в формулу (4.18), получим mотн = mнkmk' ,=1000·0,16·0,87=139. Ответ. mотн=139. Пример 4.10.Рассчитать относительную магнитную проницаемость μотн ииндуктивность L катушки на броневом магнитном сердечнике при следующих исходных данных: 1) число витков катушки N=50; 2) тип сердечника – Б22; 3) внутренний диаметр сердечника D2=18,3 мм; 4) диаметр центрального керна D3=9,2 мм; 5) высота сердечника H1=13,6 мм; 6) высота окна сердечника H2 =9,4 мм; 7) материал сердечника - феррит 700НМ; 8) величина зазора между чашками lз =0,3 мм; Решение. Броневой сердечник (рис. 4.11) состоит из двух половинок (чашек) с центральным керном, в отверстие которого вставляется цилиндрический подстроечник. Обмотку выполняют на отдельной цилиндрической катушке, помещаемой во внутреннюю полость сердечника. Чашки и подстроечник изготавливают из феррита или карбонильного железа.
Промышленность выпускает большой ассортимент броневых сердечников из карбонильного железа марок Р-10 или Р-20. Применяются также прецизионные термостабильные ферриты марок 2000СНМ1, 1500НМ3, 700НМ, 50ВЧ2, 30ВЧ и 20ВЧ2. В технической документации употребляют буквенно-цифровые обозначения броневых сердечников. Сердечники, изготовленные из карбонильного железа или феррита, соответственно обозначают СБ-D1 (ГОСТ 5.704) или Б-D1; например, СБ-12а, Б-22. Наружный диаметр сердечников D1 составляет 6...48 мм. Относительная магнитная проницаемость броневого сердечника рассчитывается по формуле
где lзи lc– длины зазора между чашками и магнитной силовой линии в сердечнике, соответственно. Длина магнитной силовой линии lc рассчитывается из геометрических размеров броневого сердечника (рис. 4.11, а) по формуле lc= 2Hср + Dср = (H1 + H2) + (D1 – D3). (4.20) Индуктивность катушки с броневым сердечником рассчитывается по формуле: L = ALN2,мкГ, (4.21) где постоянная AL определяет индуктивность одного витка (коэффициент индуктивности ):
где lc– см; Sc– площадь сечения магнитной цепи, см2:
1. Определяем относительную магнитную проницаемость сердечника mотн. Первоначально по формуле (4.20) рассчитываем длину магнитной силовой линии lc: lc= (13,6 + 9,4) + (22 – 9,2)=35,8 мм. Подставляя в формулу (4.19) исходные данные, получим
2. Для определения коэффициента индуктивности AL сначала по формуле (4.23) рассчитываем площадь сечения магнитной цепи Sc:
Подставляя исходные данные в формулу (4.22), получим
3. По формуле (4.21) рассчитываем индуктивность катушки L: L = 0,292·502 =730 мкГ. Ответ. mотн=142; L=730 мкГ. Добавим, что значения коэффициента АL приводятся в качестве справочных данных на броневые сердечники. Пример 4.11.Рассчитать индуктивность L катушки на кольцевом магнитном сердечнике при следующих исходных данных: 1) число витков катушки N=10; 2) тип сердечника – К5 3) материал сердечника - феррит 30ВЧ2. Решение. Кольцевые (тороидальные) сердечники представляют собой кольца, изготовленные из ферромагнитных материалов (рис. 4.12. Эти сердечники дают наиболее полное использование магнитных свойств из-за практически полного отсутствия рассеяния магнитного потока, создаваемого катушкой, намотанной на таком сердечнике. Относительная проницаемость кольцевого сердечника примерно равна начальной магнитной проницаемости магнитного материала, то есть mотн
Промышленность выпускает обширный ассортимент кольцевых сердечников из ферритов (ГОСТ 17141), карбонильного железа (ГОСТ 14208) и альсифера (ГОСТ 8763). В технической документации и при заказе кольцевые сердечники обозначают КDн Индуктивность катушки на кольцевом сердечнике прямоугольного сечения определяется по формуле где все размеры выражены в см. 1. Подставляя исходные данные задачи в формулу (4.24) получим Ответ. Lс=0,82 мкГ. Пример 4.12.Рассчитать индуктивность Lэ. к. экранированной катушки при следующих исходных данных: 1) индуктивность неэкранированной катушки L=140 мкГ; 2) длина катушки l=9 мм; 3) диаметр катушки Dк =15 мм; 4) диаметр экрана Dэ =25 мм. Решение. Индуктивность экранированной катушки Lэ.крассчитывается из выражения Lэ.к= L – DLэ= L(1 – kсв2), (4.25)
где L – индуктивность неэкранированной катушки; DLэ – индуктивность, “вносимая” экраном в индуктивность катушки; Для однослойных и тонких многослойных катушек коэффициент связи может быть определен по формуле
где Dки Dэ– соответственно диаметры катушки и экрана; h – коэффициент, зависящий от отношения Значения коэффициента h приведены на рис. 4.13. 1. Для расчета коэффициента связи kсв из графика h=f(
2. Подставляя значение kсв2 в формулу (4.25) получаем Lэ.к=140(1 – 0,22)=109,2 мкГ. Ответ. Lэ.к=109,2 мкГ.
Пример 4.13.Рассчитать добротность Qэ.к. экранированной катушки при следующих исходных данных: 1) частота f=0,9 МГц; 2) индуктивность экранированной катушки Lэ.к.=109 мкГ; 3) диаметр провода без изоляции d0=0,35 мм; 4) число витков обмотки N=99; 5) длина катушки l=9 мм; 6) диаметр катушки Dк =15 мм; 7) диаметр экрана Dэ =25 мм; 8) длина экрана lэ =25 мм; 9) коэффициент связи между катушкой и экраном kсв=0,47; 10) материал экрана – алюминий (rэ= 2,83×10–6 Ом×см). Решение. Присутствие экрана вызывает изменение общего сопротивления катушки Rэ.к, так как экран вносит в катушку некоторое сопротивление DRэи одновременно ослабляет эффект близости вследствие уменьшения напряженности магнитного поля около экранированной катушки. Добротность экранированной катушки выражается соотношением:
Сопротивление экранированной катушки току высокой частоты без учета вносимого сопротивления равно:
где использованы те же обозначения, что и в формуле (4.10). Вносимое сопротивление DRэ может быть определено на основании теории связанных цепей по формуле
Сопротивление экрана Rэ зависит от эффективной глубины проникновения высокочастотного тока, размеров экрана и удельного электросопротивления его стенок. Приближенно оно равно:
где rэ– удельное сопротивление материала экрана, Ом×см; pDэ– длина пути вихревого тока, см; Подставляя значение Rэиз выражения (4.30) с учетом значения xэфв формулу (4.29), получим для вносимого сопротивления DRэвыражение
где частота тока f выражается в Гц. 1. Сначала по формуле (4.28) рассчитываем значение сопротивления R'э.к. экранированной катушки току высокой частоты без учета вносимого сопротивления. Для этого из формулы (4.11) получаем значение сопротивления провода намотки постоянному току:
Параметр z рассчитываем из соотношения z = 0,106do Из графиков рис.4.7, а следует, что функция Бесселя F(3,52) Подставляя значения параметров в формулу (4.28), получим что
2. По формуле (4.31) рассчитываем величину вносимого сопротивления DRэ:
3. Подставляя полученные результаты в соотношение (4.27) рассчитываем добротность экранированной катушки:
Ответ. Qэ.к.=108. Пример 4.14.Рассчитать размеры индуктивно связанных катушек индуктивности при коаксиальном расположении катушек. Исходные данные для расчета: 1) коэффициент связи между катушками kсв=0,47; 2) диаметр внутренней катушки D2 =9 мм. Решение. Задачей конструктивного расчета катушек с трансформаторной связью является определение их конструктивных размеров исходя из значения коэффициента электромагнитной связи kсв, которое заранее известно из электрического расчета схемы. Конструктивную реализацию надлежащей связи между катушками без сердечника с погрешностью менее l1D1 = l2 D2; (4.32а) l1D2 = l2D1, (4.32б) где D1 и l1 – диаметр и длина наружной катушки; D2 и l2 – диаметр и длина внутренней катушки, очевидно D2 < D1. Приведенные графики носят общий характер, поскольку коэффициент kсв определяется относительными размерами катушек и не зависит от числа витков.
Из соотношений (4.32) вытекают два варианта размещения катушек: а) из соотношения (4.32а) следует: l1/D2 l2/D1 Из формулы (4.33а) следует, что l1 = 0,25·D2= 0,25·9=2,25 мм. Из формулы (4.33б) следует, что l2 = 0,25·D1= 0,25·12,6=3,15 мм. Таким образом, при использовании соотношения (4.32а) получается что длина l1 наружной катушки меньше длины l2 внутренней катушки. б) из соотношения (4.32б) следует: l1/D1 l2/D2 Из отношения (4.34а) следует, что l1 = 0,25·D1 =025·12,6= 3,15 мм. Из отношения (4.34б) следует, что l2 = 0,25·D2= 0,25·9=2,25 мм. Таким образом, при использовании соотношения (4.32б) получается что длина l1 наружной катушки больше длины l2 внутренней катушки Ответ. а) D1=12,6 мм, l1=2,25 мм; D2=9 мм, l2=3,15 мм; б) D1=12,6 мм, l1=3,15 мм; D2=9 мм, l2=2,25 мм. Пример 4.15.Определить расстояние m между индуктивно связанными катушками индуктивности и их длины l при смежном (соосном) расположении. Исходные данные для расчета: 1) коэффициент связи между катушками kсв=0,1; 2) диаметр катушки Dн =9 мм; 3) отношение длины катушки к диаметру катушки l/Dн=1,6. Решение.
1. По заданным значениям коэффициента связи kсв=0,1и отношения длины катушки к диаметру катушки l/Dн=1,6 на номограмме рис. 4.15 восстанавливаем перпендикуляры к координатным осям из соответствующих точек. 2. Точка пересечения перпендикуляров соответствует значению m/Dн m=0,1Dн=0,1·9= 0,9 мм Ответ. m=0,9 мм; l=1,6·9=14,4 мм. Проектирование элементов катушек индуктивности С сердечниками Пример 4.16.Рассчитать относительную магнитную проницаемость mотн и число витков N катушки индуктивности с цилиндрическим сердечником. Исходные данные для расчета: 1) тип сердечника СЦГ 2,86 2) материал - феррит 700НМ; 3) размеры катушки: Dк = 5 мм, l = 9 мм. Решение. Расчетная схема катушки с цилиндрическим сердечником представлена на рис. 4.16. На этом рисунке Dк и Dc – диаметры катушки и сердечника, l и lс – длины катушки и сердечника, соответственно.
Lр = Lн/mотн, (4.35) где mотн – относительная магнитная проницаемость сердечника. Составляем отношения Dк/Dс = 5/2,86 mотн = 700×0,24×0,95 По формуле (4.35) определяем расчетную индуктивность катушки: Lр = 100/160 = 0,625 мкГ. Расчетное значение индуктивности невелико, поэтому принимаем решение проектировать однослойную катушку с рядовой намоткой. 2. Расчет числа витков катушки производится по формуле, которая следует из выражения (4.4):
где Lр выражается в мкГ, Dк – в см. Составляем отношение l/Dк = 9/5 = 1,8 и из графика рис. 4.3 определяем значение Lo = 4,2. По формуле (4.36) рассчитываем число витков катушки N:
Ответ. mотн =160 мм; l=17,3. Пример 4.17.Определить оптимальный диаметр провода намотки dопт цилиндрической катушки индуктивности при следующих исходных данных: 1) рабочая частота f=3 МГц; 2) размеры катушки: Dк = 5 мм, l = 9 мм; 3) число витков катушки N=17,3. Решение. Оптимальный диаметр провода обмотки катушки для частот f
где частота f выражается в Гц; значение zопт находится из графика zопт = f(Y), представленного на рис. 4.17.
Величина аргумента Y на рис. 4.17 рассчитывается по формуле
где значение коэффициента При значениях аргумента Y, выходящих за пределы графика рис. 4.23 (Y<0,3 и Y>2000), величина zопт рассчитывается по следующим формулам:
1. Сначала из рис. 4.7, б определяем значение коэффициента k = f(9/5) = f(1,8) = 2,5. Затемпо формуле (4.38) раcсчитываем величину аргумента Y:
Поскольку величина аргумента Y<0,3, то значение параметра zопт рассчитываем по формуле (4.39):
2. Значение оптимального диаметра провода dопт рассчитываем из соотношения (4.37):
В качестве провода намотки выбираем эмалированный провод ПЭВ со стандартным диаметром dиз = 0,41 мм. По формуле l = Nadиз, где a = 1,2 – коэффициент неплотности укладки провода, проведем поверочный расчет длины намотки: l = 17,3×1,2×0,41 Ответ. dотн =0,37 мм dиз =0,41 мм. Пример 4.18.Определить оптимальный диаметр dопт провода намотки цилиндрической однослойной катушки индуктивности метрового диапазона при следующих исходных данных: 1) рабочая частота f=140 МГц; 2) размеры катушки: Dк = 5 мм, l = 9 мм; 3) шаг намотки t=1 мм. Решение.
Оптимальный диаметр провода однослойных катушек метрового диапазона радиоволн (f >10 МГц) зависит от шага намотки t и отношения размеров катушки
где При выбранном диаметре провода без изоляции do выражение (4.41) можно использовать для расчета шага намотки t. 1. Из графика рис. 4.18 определяем значение коэффициента k1: k1=f(9/5) = f(1,8)=1,8. 2. Подставляя значения исходных данных в формулу (4.41) получим
Ответ. dотн =0,56 мм. Пример 4.19.Определить добротность цилиндрической катушки индуктивности с сердечником при следующих исходных данных: 1) рабочая частота f=3 МГц; 2) тип сердечника СЦГ 2,86 3) материал - феррит 700НМ; 4) магнитные потери в сердечнике tgdm =1,28×10–2; 5) размеры катушки: Dк = 5 мм, l = 9 мм; 6) число витков катушки N=17,3 7) потери в изоляции провода tgdиз = 1·10–2. Решение. Добротность катушки на частоте f определяется по формуле:
где Lн – индуктивность катушки, Г; Rм – сопротивление провода току высокой частоты, Ом; RСL– сопротивление потерь в собственной емкости катушки, Ом; Rm – сопротивление потерь, вносимое сердечником, Ом. 1. Предварительно по формуле (4.10) определяем сопротивление провода катушки току высокой частоты. В выражении (4.10) функции F(z) и G(z) находим из графика рис. 4.7, а где
Подставляя полученные значения Rмо, F(z) и G(z) в формулу (4.10), получим:
2. По формуле (4.8) рассчитаем сопротивление потерь в собственной емкости RCL: RCL= (6,28×3×106)3 (100×10–6)20,3×10–1210–2 = 0,2 Ом. В формуле (4.8) значение собственной емкости катушки CL = 0,5×0,5 3. Из соотношения (4.17) рассчитываем значение сопротивления потерь Rm:
4. Подставляя значения Rм, RCLи Rm в формулу (4.42), получим, что добротность спроектированной катушки равна
Таким образом, основной вклад в снижение добротности вносит составляющая, обусловленная вносимым сопротивлением магнитных потерь Rm. Ответ. Q =76,8. Пример 4.20.Рассчитать число витков и подобрать тип провода катушки индуктивности на броневом сердечнике со следующими параметрами: 1) рабочая частота f = 3 МГц; 2) индуктивность L = 100 3) броневой сердечник типоразмера Б11; 4) материал сердечника - феррит 50ВЧ с mн = 45; 5) габаритные размеры сердечника (рис. 4.11): наружный диаметр D1 = 1,1 см, внутренний диаметр D2 = 0,94 см, диаметр центрального керна D3 = 0,47 см, высота сердечника H1 = 0,64 см, высота окна H2 = 0,44 см; 6) относительная магнитная проницаемость сердечника mотн = 38,8. Решение. Расчет числа витков катушки производится по формуле, которая следует из выражения (4.21):
где Lн – номинальная индуктивность катушки, мкГ; АL – постоянная, мкГ, рассчитывается по формуле (4.22). 1. Первоначально по формуле (4.20) рассчитываем длину магнитной силовой линии lc: lc= (H1 + H2) + (D1 – D3)= = (0,64 + 0,44) + (1,1 – 0,47)=1,71 см. 2. По формуле (4.23) рассчитываем площадь сечения магнитной цепи Sc:
3. По формуле (4.22) рассчитываем постоянную AL (индуктивность одного витка):
4. Подставляя полученное значение AL в формулу (4.43) для числа витков катушки, получим
5. Значения оптимального диаметра провода обмотки катушек на броневом сердечнике определяются по специально построенным графикам. В качестве примера на рис. 4.19 представлены графики Q = j(f) частотных зависимостей добротности катушек на сердечниках Б11 из феррита 50ВЧ2 при lз = 0,2 мм, намотанных проводами различных марок. Характерным для этих графиков является заметно выраженная зависимость добротности от частоты.
В соответствии с рис. 4.19 выбираем в качестве намоточного провода провод марки ЛЭШО 10 6. Выполняем поверочный расчет размещения обмотки катушки на броневом сердечнике. Для этого по формуле n = H2/adиз, полагая a = 1,2, рассчитываем количество витков n в одном ряду:
Затем определяем число рядов обмотки: m = N/n = 52/11 = 4,7. Глубина намотки t = madиз = 4,7×1,2×0,33 = 1,9 мм. Поскольку ширина окна сердечника СБ11 равна D2 – D3 = 9,4 – 4,7 = 4,7 мм и больше глубины t, то делаем вывод о том, что обмотка катушки размещается на сердечнике. Ответ. N=52; тип провода намотки ЛЭШО 10 Пример 4.21.Рассчитать добротность катушки индуктивности на броневом сердечнике с параметрами из примера 4.20. Дополнительные условия: толщина стенки каркаса катушки dкар=0,5 мм, собственная емкость катушки СL=2 пФ, tg δиз=10-3. Решение. Добротность катушки индуктивности определяется по формуле (4.42). Сопротивление обмотки катушки току высокой частоты рассчитывается по формуле Rм=kпэ Rмо, (4.44) где kпэ=d0/4xэф – коэффициент, учитывающий увеличение сопротивления провода за счет поверхностного эффекта; d0 – полный наружный диаметр литцендрата, см; 1. Рассчитываем средний диаметр катушки по формуле Dср=D3+2 dкар+t=4,7+2·0,5+1,9=7,6 мм 2. Принимая значение коэффициента скручивания жилок а=1,04, определяем сопротивление обмотки постоянному току Rм по формуле (4.14), где размеры берутся в мм:
3. По формуле (4.13) рассчитываем полный наружный диаметр литцендрата: d0=1,35·0,005· 4. Определяем эффективную глубину проникновения электромагнитного поля в медный проводник:
5. По формуле (4.44) рассчитываем сопротивление провода току высокой частоты
6. По формуле (4.7) рассчитываем сопротивление потерь в собственной емкости катушки:
7. По формуле (4.17) рассчитываем активное сопротивление потерь в сердечнике: Rm=2·3,14·3·106·100·10-6·4,7·10-3= 8,86 Ом. 8. Подставив в формулу (4.42) полученные значения Rм, RCL, Rm, получаем
Ответ. Q =178. Рассчитанное
Поиск по сайту: |
 – напряженность переменного магнитного поля, создаваемого током в катушке, А/м;
– напряженность переменного магнитного поля, создаваемого током в катушке, А/м; .
. . (4.2)
. (4.2)
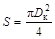 .
. ×10–3, мкГ, (4.3)
×10–3, мкГ, (4.3) мкГ.
мкГ. 0,53 мГ.
0,53 мГ.



 =3 Ом.
=3 Ом.
 10–6¼10–2 Г – индуктивность катушки, RL
10–6¼10–2 Г – индуктивность катушки, RL  , (4.6)
, (4.6)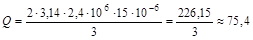 .
. , где U=IωL; tgdиз – тангенс угла диэлектрических потерь изоляции провода и каркаса катушки; СL – собственная емкость катушки. В результате получаем, что
, где U=IωL; tgdиз – тангенс угла диэлектрических потерь изоляции провода и каркаса катушки; СL – собственная емкость катушки. В результате получаем, что .
. , Ом, (4.7)
, Ом, (4.7) Ом.
Ом. Ом.
Ом. 10 МГц сопротивление провода катушки индуктивности току высокой частоты рассчитывается по следующей формуле:
10 МГц сопротивление провода катушки индуктивности току высокой частоты рассчитывается по следующей формуле: . (4.10)
. (4.10) ; do – диаметр провода намотки без изоляции, см; f – частота тока, протекающего через катушку, Гц; k = f(l/D) – коэффициент; l – длина; Dср – средний диаметр обмотки, см; N – число витков катушки.
; do – диаметр провода намотки без изоляции, см; f – частота тока, протекающего через катушку, Гц; k = f(l/D) – коэффициент; l – длина; Dср – средний диаметр обмотки, см; N – число витков катушки. , Ом, (4.11)
, Ом, (4.11) Ом
Ом =7,4.
=7,4.
 Ом.
Ом. , (4.12)
, (4.12) , см; (4.13)
, см; (4.13) , Ом. (4.14)
, Ом. (4.14) Ом
Ом см.
см.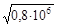

 Ом.
Ом. , Ом (4.15)
, Ом (4.15) Ом.
Ом. , (4.16)
, (4.16)

 . Диаметр Dc сердечников для подстройки катушек (подстроечников) составляет 1,8¼9 мм, длина lc сердечников равна 10¼20 мм. Длина гладких сердечников, предназначенных для устройства магнитных антенн, достигает 80...120 мм, форма может быть как цилиндрической, так и прямоугольной.
. Диаметр Dc сердечников для подстройки катушек (подстроечников) составляет 1,8¼9 мм, длина lc сердечников равна 10¼20 мм. Длина гладких сердечников, предназначенных для устройства магнитных антенн, достигает 80...120 мм, форма может быть как цилиндрической, так и прямоугольной.
 Для получения необходимых электромагнитных параметров и повышения стабильности магнитных свойств между чашками в центральный керн броневого сердечника вводят нормированный зазор длиной lз=0,1¼0,3 мм.
Для получения необходимых электромагнитных параметров и повышения стабильности магнитных свойств между чашками в центральный керн броневого сердечника вводят нормированный зазор длиной lз=0,1¼0,3 мм. , (4.19)
, (4.19) , мкГ. (4.22)
, мкГ. (4.22) . (4.23)
. (4.23)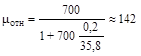 .
.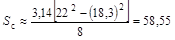 мм2=0,585 см2.
мм2=0,585 см2. мкГ.
мкГ. 2
2  mн.
mн. Кольцевые сердечники применяют для широкополосных согласующих трансформаторов, для контуров промежуточной частоты радиоприемников, для контуров, перестройка частоты которых производится подмагничиванием, для высокочастотных дросселей. К недостаткам катушек на кольцевых сердечниках относятся невозможность подстройки частоты, а также необходимость применения специального оборудования для намотки.
Кольцевые сердечники применяют для широкополосных согласующих трансформаторов, для контуров промежуточной частоты радиоприемников, для контуров, перестройка частоты которых производится подмагничиванием, для высокочастотных дросселей. К недостаткам катушек на кольцевых сердечниках относятся невозможность подстройки частоты, а также необходимость применения специального оборудования для намотки. Dвн
Dвн  , мкГ, (4.24)
, мкГ, (4.24)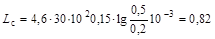 мкГ.
мкГ.
 – коэффициент связи между катушкой и экраном, который определяется соотношением геометрических размеров экрана и катушки, величина 0<kсв<1; M – взаимная индуктивность между катушкой и экраном.
– коэффициент связи между катушкой и экраном, который определяется соотношением геометрических размеров экрана и катушки, величина 0<kсв<1; M – взаимная индуктивность между катушкой и экраном.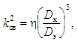 (4.26)
(4.26) , где l – длина намотки катушки.
, где l – длина намотки катушки.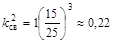 .
.
 . (4.27)
. (4.27) , (4.28)
, (4.28) . (4.29)
. (4.29) , (4.30)
, (4.30) – эффективная глубина проникновения тока, см; f – частота в Гц; lэxэф– активное (проводящее ток) сечение, см2.
– эффективная глубина проникновения тока, см; f – частота в Гц; lэxэф– активное (проводящее ток) сечение, см2. (4.31)
(4.31) Ом.
Ом.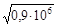 =3,52.
=3,52. Ом.
Ом. Ом.
Ом. .
.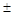 5% от заданной величины kсв осуществляют с помощью номограмм на рис. 4.14, когда катушки расположены одна в другой и выполняются соотношения
5% от заданной величины kсв осуществляют с помощью номограмм на рис. 4.14, когда катушки расположены одна в другой и выполняются соотношения 1. По заданному значению коэффициента связи kсв=0,47 на номограмме рис. 4.14 находим точки пересечения горизонтальной прямой, восстановленной из точки 0,47 с кривыми, соответствующими различным значениям отношений диаметров наружной и внутренней катушек: D1/D2 = 1,1; 1,2; 1,3; 1,4. В качестве варианта выберем, например, точку пересечения горизонтали с кривой соответствующую отношению D1/D2 = 1,4. Этому значению соответствует диаметр наружной катушки D1 = 1,4·D2 = 1,4·9=12,6 мм.
1. По заданному значению коэффициента связи kсв=0,47 на номограмме рис. 4.14 находим точки пересечения горизонтальной прямой, восстановленной из точки 0,47 с кривыми, соответствующими различным значениям отношений диаметров наружной и внутренней катушек: D1/D2 = 1,1; 1,2; 1,3; 1,4. В качестве варианта выберем, например, точку пересечения горизонтали с кривой соответствующую отношению D1/D2 = 1,4. Этому значению соответствует диаметр наружной катушки D1 = 1,4·D2 = 1,4·9=12,6 мм. Зависимость коэффициента связи между двумя смежными цилиндрическими катушками одинаковой длины l и диаметра Dк от расстояния m между ними показана на номограмме, представленной на рис. 4.15. Ограничений на соотношение между числами витков в обмотках катушек нет.
Зависимость коэффициента связи между двумя смежными цилиндрическими катушками одинаковой длины l и диаметра Dк от расстояния m между ними показана на номограмме, представленной на рис. 4.15. Ограничений на соотношение между числами витков в обмотках катушек нет. 12 мм;
12 мм; 1. После выбора материала и типоразмера Dc
1. После выбора материала и типоразмера Dc 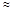 1,75 и l/Dс = 9/2,86
1,75 и l/Dс = 9/2,86 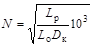 , (4.36)
, (4.36) .
. , см, (4.37)
, см, (4.37)
 , (4.38)
, (4.38) определяется из рис. 4.7, б.
определяется из рис. 4.7, б. при Y<0,3, (4.39)
при Y<0,3, (4.39) при Y>2000. (4.40)
при Y>2000. (4.40)
 .
. см
см 
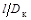 :
: , (4.41)
, (4.41) – коэффициент, значения которого даны на рис. 4.18.
– коэффициент, значения которого даны на рис. 4.18. мм.
мм. , (4.42)
, (4.42) = 0,106×3,7×10–2×1,732×103 = 6,79. Получаем F(z) = 2,67; G(z) = 1,07. Значение сопротивления провода постоянному току рассчитываем по формуле (4.11):
= 0,106×3,7×10–2×1,732×103 = 6,79. Получаем F(z) = 2,67; G(z) = 1,07. Значение сопротивления провода постоянному току рассчитываем по формуле (4.11): Ом.
Ом.
 24,1 Ом.
24,1 Ом.
 , (4.43)
, (4.43) =
=  см2.
см2. мкГ.
мкГ. .
.
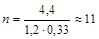 .
. , см – эффективная глубина проникновения электромагнитного поля в проводник; m
, см – эффективная глубина проникновения электромагнитного поля в проводник; m  Ом.
Ом. =2,13·10-2 см.
=2,13·10-2 см. см.
см. Ом.
Ом.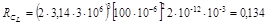 Ом.
Ом. .
.