 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
ОБРАЗЕЦ ИНДИВИДУАЛЬНОГО ЗАДАНИЯ. ПО ТЕХНИКЕ ДИФФЕРЕНЦИРОВАНИЯ ⇐ ПредыдущаяСтр 2 из 2
ПО ТЕХНИКЕ ДИФФЕРЕНЦИРОВАНИЯ И ВЫЧИСЛЕНИЮ ПРЕДЕЛОВ
Задача №1
Вычислить производные следующих функций. 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16)
Задача №2
Вычислить производные 1) 2) 3) 4) Задача №3
Исследовать функции на непрерывность. Указать точки разрыва и характер разрыва.
1) 2) 3) 4)
Задача №4
Найти пределы функций, не используя правило Лопиталя. 1) 2) 3) 4) 5) 6) 7)
8) 9) 10) 11) 12) 13) 14)
Задача №5
Найти следующие пределы, используя правило Лопиталя. 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11)
Решение задачи №1
Для решения примеров на вычисление производной необходимо выучить наизусть правила дифференцирования, таблицу производных, а также нужно хорошо разбираться в порядке следования операций в математическом выражении. Весь этот материал изложен в лекции 1, где также вычислено большое число производных и приведены замечания, полезные при дифференцировании. 1) 2)
3)
4)
5) 6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
Решение задачи №2
Примеры 1) и 2) связаны с вычислением производной функции, заданной неявно. Именно, если независимая переменная 1) Дифференцируем обе части уравнения
2)
12) Рассмотрим систему Находим Получаем: Ответ:
13) Пусть Получаем:
Ответ:
Решение задачи №3
1) Область определения функции
Итак, у функции существуют и левосторонний предел Рассмотрим точку
Значение функции в точке Итак, функция непрерывна на множестве
2) Область определения функции
Поэтому точка Итак, функция непрерывна на множестве 3) Область определения функции Найдем односторонние пределы функции в точке
Итак, точка Рассмотрим точку
Итак, точка Таким образом, функция непрерывна на множестве 4) Область определения функции
Итак, точка Функция непрерывна на множестве
Решение задачи №4
Перед решением примеров данного раздела следует изучить лекции 4 и 5. 1)
2) Вычислим отдельно предел числителя и знаменателя. Имеем:
Поэтому, из соотношения (12) на стр.20 получаем:
3) По теореме 6 на стр. 18 при
4) Из цепочки эквивалентностей (8) на стр. 17 получаем
5) Решение этого примера аналогично решению примера 4. При
6) При
7) Имеем: В процессе решения мы применили эквивалентность 8) Здесь имеет место неопределенность
9) Разделив и умножив дробь на сопряженные выражения для числителя и знаменателя, получаем:
10) Решение этого примера совершенно аналогично решению примера 3. А именно, используя эквивалентность (9), получаем:
11) Сперва применяем формулу преобразования суммы синусов в произведение, а затем используем 4–е свойство предела функции (стр.13):
12) Решение аналогично решению примеров 3 и 10:
13) В процессе решения мы применили эквивалентность 14) Перед решением этого примера следует просмотреть пример 19 на стр. 22. Обозначим
Решение задачи №5
Для решения примеров этого раздела необходимо изучить теорему Лопиталя (см. теорему 9 на стр. 20-21). Правило Лопиталя применяют повторно, пока не устранится неопределенность или обнаружится, что нужные пределы не существуют. 1) 2) 3) 4) 5) 6) 7)
8) 9)
10) 11) Обозначим
Окончательно:
Поиск по сайту: |
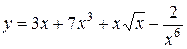
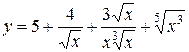
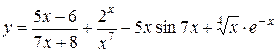


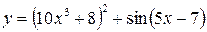
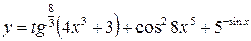
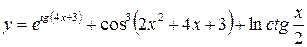
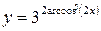
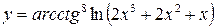
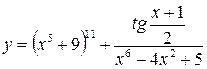

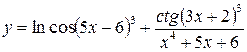
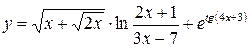


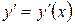 функций, заданных неявно, и функций, заданных параметрически.
функций, заданных неявно, и функций, заданных параметрически.
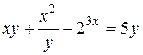



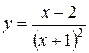
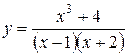
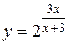
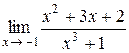
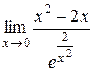
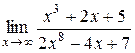
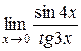
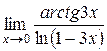
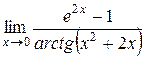

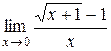
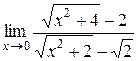
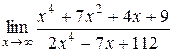

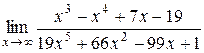



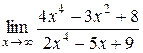
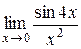
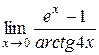
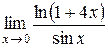

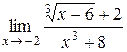
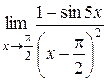
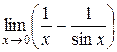
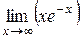

 .
.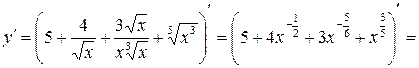

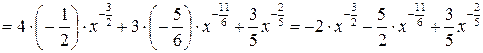 .
.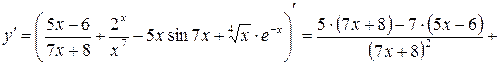
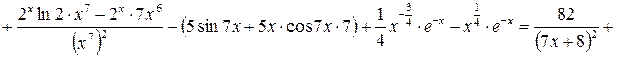
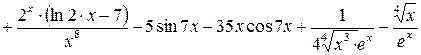 .
.
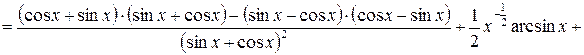

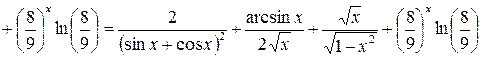 .
. .
.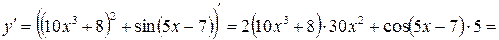
 .
.

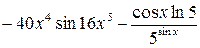 .
.
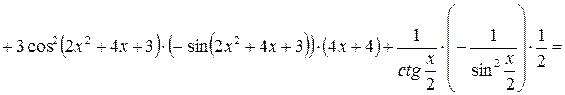
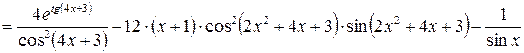 .
.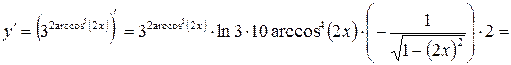 .
.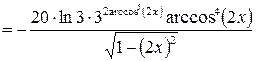 .
.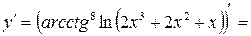
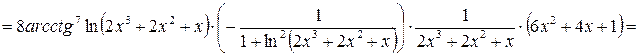
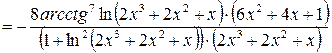 .
.
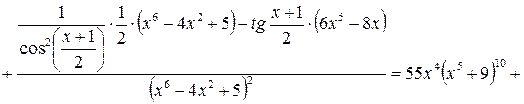
 .
.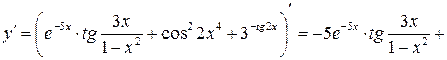

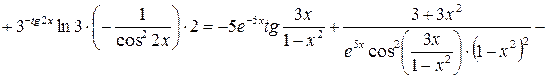
 .
.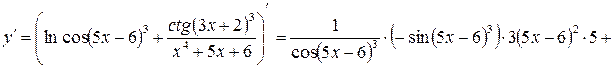

 .
.
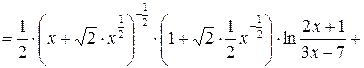

 .
.
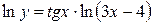

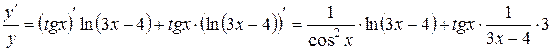
 .
.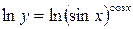



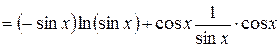
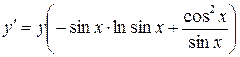
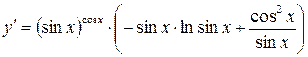 .
.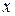 и функция
и функция 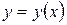 связаны уравнением вида
связаны уравнением вида 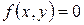 , которое не разрешимо в явном виде относительно
, которое не разрешимо в явном виде относительно 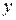 , то
, то  .
.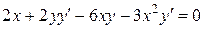
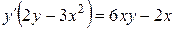
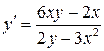 .
.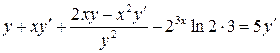
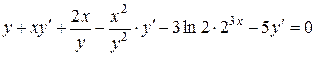
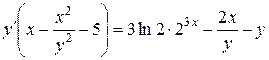
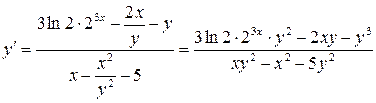 .
.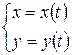 , где
, где 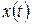 и
и 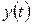 – дифференцируемые функции и
– дифференцируемые функции и 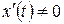 , определяет
, определяет 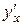 существует и вычисляется по формуле:
существует и вычисляется по формуле: 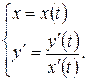
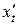 и
и 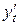 :
:  ,
, 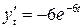 .
. .
.
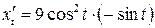 ,
, 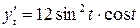 .
. .
.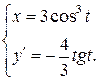
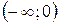 ,
, 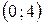 ,
, 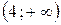 функция непрерывна. Разрывы возможны лишь в точках
функция непрерывна. Разрывы возможны лишь в точках 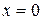 и
и 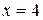 . Найдем односторонние пределы функции в точке
. Найдем односторонние пределы функции в точке 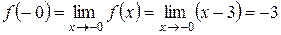 ,
, .
.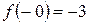 , и правосторонний предел
, и правосторонний предел 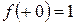 , но между собой они не равны. Поэтому точка
, но между собой они не равны. Поэтому точка 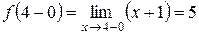 ,
,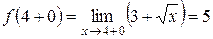 .
.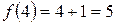 . Так как
. Так как  , то в точке
, то в точке  .
.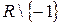 . На интервалах
. На интервалах  ,
, 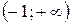 функция непрерывна. Поэтому разрыв возможен только в точке
функция непрерывна. Поэтому разрыв возможен только в точке 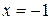 . Найдем односторонние пределы функции в точке
. Найдем односторонние пределы функции в точке 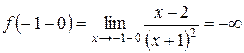 ,
, .
.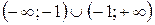 .
.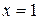 :
: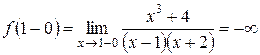 ,
, .
. :
: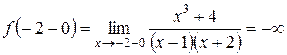 ,
, .
.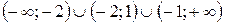 .
. ,
, 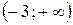 функция непрерывна. Поэтому разрыв возможен только в точке
функция непрерывна. Поэтому разрыв возможен только в точке 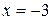 . Найдем односторонние пределы функции в точке
. Найдем односторонние пределы функции в точке 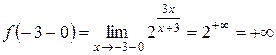 ,
,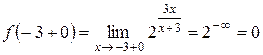 .
. .
. Здесь имеет место неопределенность
Здесь имеет место неопределенность 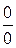 . Разложим на множители числитель и знаменатель дроби:
. Разложим на множители числитель и знаменатель дроби: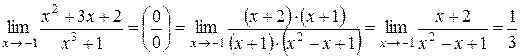 .
.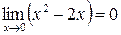 ,
, 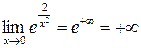 .
.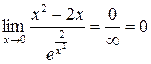 .
. многочлен эквивалентен своему одночлену с наивысшей степенью. По теореме 7 на стр. 18 числитель и знаменатель можно заменить на эквивалентные им функции. Имеем:
многочлен эквивалентен своему одночлену с наивысшей степенью. По теореме 7 на стр. 18 числитель и знаменатель можно заменить на эквивалентные им функции. Имеем: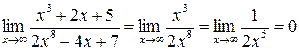 .
.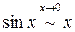 и
и 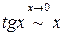 . Заменяя
. Заменяя 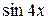 эквивалентной ей функцией
эквивалентной ей функцией 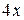 и
и 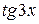 – функцией
– функцией  , получаем:
, получаем: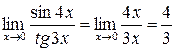 .
.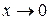
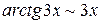 ,
, 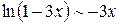 . Заменяя числитель и знаменатель эквивалентными им функциями, получаем:
. Заменяя числитель и знаменатель эквивалентными им функциями, получаем: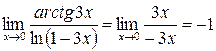 .
. ,
, 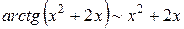 . Получаем:
. Получаем: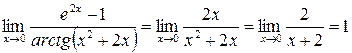 .
.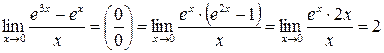 .
.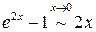 .
.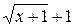 . Получаем:
. Получаем: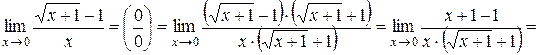
 .
.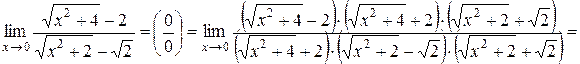
 .
.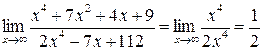 .
.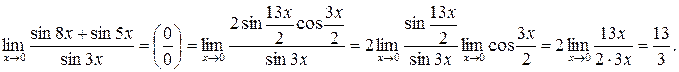
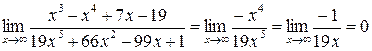 .
. .
.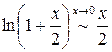 .
.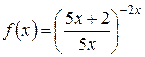 и прологарифмируем данное равенство. Получаем:
и прологарифмируем данное равенство. Получаем: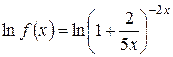
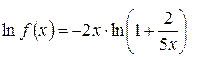
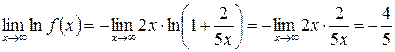 (мы применили эквивалентность
(мы применили эквивалентность 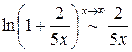 ). Перейдем теперь от логарифма к самой функции:
). Перейдем теперь от логарифма к самой функции: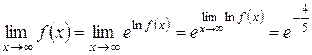 .
.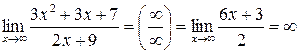 .
.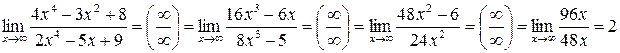 .
. .
.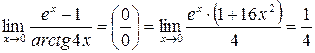 .
.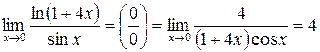 .
.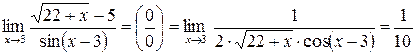 .
.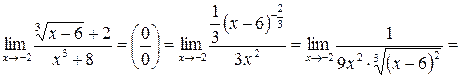
 .
. .
.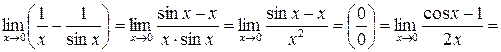
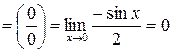 .
. .
.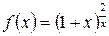 . Имеем:
. Имеем:  . Далее:
. Далее: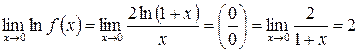 .
. .
.