ДОКАЗАТЕЛЬСТВА ФОРМУЛ ДИФФЕРЕНЦИРОВАНИЯ
ТЕОРИЯ ПРЕДЕЛОВ
И ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Раздел 1. Вычисление производных и пределов
Курс лекций
и образец решения индивидуального задания
для бакалавров 1-го курса
очной формы обучения
Ростов-на-Дону
УДК 517(07)
Теория пределов и дифференциальное исчисление. Раздел 1. Вычисление производных и пределов. Курс лекций и образец решения индивидуального задания для бакалавров 1-го курса очной формы обучения. – Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 39 с.
Изложен курс лекций по теории пределов и дифференциальному исчислению. Приведен образец решения индивидуального задания «Техника дифференцирования и вычисление пределов».
Лекции 1 – 6 составлены И.В. Павловым. Образец решения индивидуального задания составлен О.В. Назарько и адаптирован к курсу лекций И.В.Павловым.
Предназначены для бакалавров 1-го курса очной формы, проходящих обучение на кафедре высшей математики РГСУ, а также на математических кафедрах других вузов.
Электронная версия методических указаний находится в библиотеке, ауд. 224.
УДК 517(07)
| Составители:
| д-р физ.-мат. наук, проф.
И.В. Павлов
ассист. О.В. Назарько
| |
Рецензенты:
|
канд. физ.-мат. наук, доц.
А.М. Можаев
канд. физ.-мат. наук, доц.
Г.А. Власков
|
Редактор Т.М. Климчук
Доп. план 2011 г., поз. 179
Подписано в печать 12.07.11. Формат 60´84/16. Бумага писчая. Ризограф.
Уч.-изд.л. 3,0. Тираж 50 экз. Заказ 381
Редакционно-издательский центр
Ростовского государственного строительного университета
344022, Ростов-на-Дону, ул. Социалистическая, 162.
© Ростовский государственный
строительный университет, 2011
ВВОДНАЯ ЛЕКЦИЯ: ТЕХНИКА ДИФФЕРЕНЦИРОВАНИЯ
Лекция 1
В данном разделе мы напомним известные из средней школы факты, связанные с вычислением производной. Все эти утверждения будут доказаны нами после изучения теории пределов. Начнем с формального определения производной.
Пусть функция  определена на открытом интервале определена на открытом интервале 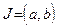 действительной прямой R, точка действительной прямой R, точка 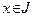 и число и число 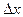 (называемое приращением независимой переменной x) таково, что (называемое приращением независимой переменной x) таково, что 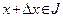 . При этом выражение . При этом выражение 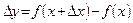 называют приращением данной функции в точке называют приращением данной функции в точке 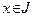 . .
Определение 1. Производной 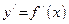 функции функции  в точке в точке 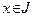 называется предел отношения приращения функции в точке называется предел отношения приращения функции в точке 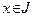 к приращению независимой переменной, когда приращение к приращению независимой переменной, когда приращение 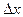 независимой переменной стремится к нулю, то есть независимой переменной стремится к нулю, то есть
|
| 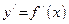 = =  . .
|
(1)
| Функция  называется дифференцируемой на интервале называется дифференцируемой на интервале 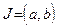 , если она имеет производную в каждой точке этого интервала. Процесс вычисления производной называется дифференцированием. , если она имеет производную в каждой точке этого интервала. Процесс вычисления производной называется дифференцированием.
Для того, чтобы освоить технику вычисления производной, необходимо знать правила дифференцирования, таблицу производных элементарных функций, а также уметь четко определять порядок действий в математическом выражении.
Правила дифференцирования
1. Производная постоянной функции равна нулю, то есть если 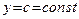 , то , то
|
| 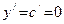 . .
|
| 2. Производная суммы двух функций равна сумме производных этих функций, то есть если 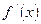 и и 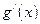 существуют, то существуют, то
|
| 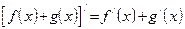 . .
|
| 3. Постоянный множитель можно вынести за знак производной, то есть если  , а , а 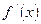 существует, то существует, то
|
| 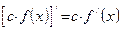 . .
|
| 4. Производная произведения двух функций равна производной первой функции, умноженной на вторую, плюс первая функция, умноженная на производную второй; то есть если 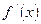 и и 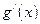 существуют, то существуют, то
|
| 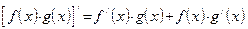 . .
|
| 5. Производная частного двух функций равна дроби, знаменатель которой равен квадрату знаменателя исходной дроби, а в числителе которой стоит производная числителя исходной дроби, умноженная на ее знаменатель, минус числитель исходной дроби, умноженный на производную ее знаменателя; то есть если 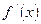 и и 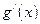 существуют и существуют и 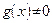 , то , то
|
|  . .
|
| 6. Производная сложной функции (цепное правило): если  , где в свою очередь , где в свою очередь  , и если , и если 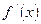 и и 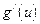 существуют, то существуют, то
|
|  . .
|
|
Таблица производных элементарных функций
| Производные степенной, показательной и логарифмической функций
| Производные тригонометрических функций
| Производные обратных тригонометрических функций
|  (где (где  ) )
| 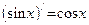
| 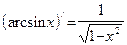
| 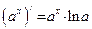 (где (где 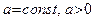 ) )
| 
| 
|  (где (где 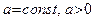 , , 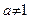 ) )
| 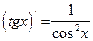
| 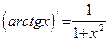 
| 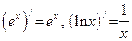 (частные случаи предыдущих двух формул при (частные случаи предыдущих двух формул при  , где e – натуральное число) , где e – натуральное число)
|

|
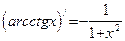
|
Порядок действий в математическом выражении
и дифференцирование сложных функций
Рассмотрим две функции:  и и 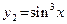 . Эти функции очень похожи. Для правильного их дифференцирования нужно отчетливо выделить операции, которые производятся над переменной x в данных математических выражениях. У первой функции переменная x сначала возводится в куб, а затем на полученный результат действует функция синус. Таким образом, . Эти функции очень похожи. Для правильного их дифференцирования нужно отчетливо выделить операции, которые производятся над переменной x в данных математических выражениях. У первой функции переменная x сначала возводится в куб, а затем на полученный результат действует функция синус. Таким образом,  . Наоборот, у второй функции переменная x сначала подвергается действию функции синус, а затем результат возводится в куб, то есть . Наоборот, у второй функции переменная x сначала подвергается действию функции синус, а затем результат возводится в куб, то есть 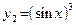 . Найдем производные этих функций, применяя цепное правило и таблицу производных. Заметим, что начинать дифференцирование нужно с последней операции, затем дифференцируют предпоследнюю операцию и, действуя таким образом, заканчивают производной первой операции. . Найдем производные этих функций, применяя цепное правило и таблицу производных. Заметим, что начинать дифференцирование нужно с последней операции, затем дифференцируют предпоследнюю операцию и, действуя таким образом, заканчивают производной первой операции.
Последней операцией функции  является операция синус, производная которой есть косинус, поэтому первым звеном цепного правила является функция является операция синус, производная которой есть косинус, поэтому первым звеном цепного правила является функция 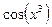 . При этом у полученной нами функции сохранился аргумент, которым обладал синус. Предпоследней операцией у рассматриваемой функции является возведение в куб (эта операция в данном примере одновременно является первой). Поэтому второе (и заключительное) звено цепного правила будет производная степенной функции . При этом у полученной нами функции сохранился аргумент, которым обладал синус. Предпоследней операцией у рассматриваемой функции является возведение в куб (эта операция в данном примере одновременно является первой). Поэтому второе (и заключительное) звено цепного правила будет производная степенной функции 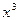 , то есть функция , то есть функция  . Руководствуясь формулой 6 правил дифференцирования, окончательно получаем : . Руководствуясь формулой 6 правил дифференцирования, окончательно получаем : 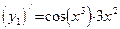 . .
Последней операцией функции 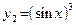 является возведение в куб, поэтому у ее производной первым звеном будет функция является возведение в куб, поэтому у ее производной первым звеном будет функция  . Отметим, что так как у исходной функции аргументом, который возводился в куб, был . Отметим, что так как у исходной функции аргументом, который возводился в куб, был 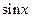 , то этот аргумент сохранился и в первом звене дифференцирования. Предпоследней (и одновременно первой) операцией рассматриваемой функции является синус, поэтому второе звено будет равно , то этот аргумент сохранился и в первом звене дифференцирования. Предпоследней (и одновременно первой) операцией рассматриваемой функции является синус, поэтому второе звено будет равно  . Окончательно получаем: . Окончательно получаем:  . .
Продифференцируем теперь сложную функцию, состоящую из трех операций, а именно функцию 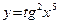 . Вычленим составляющие эту функцию простые операции: . Вычленим составляющие эту функцию простые операции: 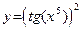 . Здесь первая операция – возведение переменной x в пятую степень, вторая операция – взятие тангенса от полученного результата и, наконец, последняя операция – возведение всего, что получилось, в квадрат. При дифференцировании цепное правило даст три звена. Первое звено получим, дифференцируя последнюю операцию. Оно будет состоять из функции . Здесь первая операция – возведение переменной x в пятую степень, вторая операция – взятие тангенса от полученного результата и, наконец, последняя операция – возведение всего, что получилось, в квадрат. При дифференцировании цепное правило даст три звена. Первое звено получим, дифференцируя последнюю операцию. Оно будет состоять из функции  . Второе звено – производная предпоследней операции – равно . Второе звено – производная предпоследней операции – равно 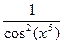 . И, наконец, последнее звено есть функция . И, наконец, последнее звено есть функция  . В результате имеем: . В результате имеем: 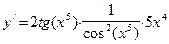 . .
Вычислим производную еще более сложной функции 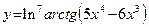 . Здесь первой операцией целесообразно считать многочлен . Здесь первой операцией целесообразно считать многочлен 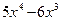 . Вторая операция – это взятие арктангенса от многочлена, третья операция – вычисление натурального логарифма, четвертая операция – возведение всего полученного в седьмую степень. Применяя цепное правило, получаем: . Вторая операция – это взятие арктангенса от многочлена, третья операция – вычисление натурального логарифма, четвертая операция – возведение всего полученного в седьмую степень. Применяя цепное правило, получаем: 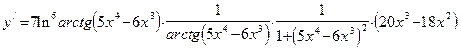 . .
Некоторые замечания, полезные при дифференцировании
1. Если нужно продифференцировать функцию, содержащую радикалы, то перед дифференцированием эти радикалы следует перевести в дробные степени. Например, пусть 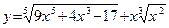 . Сначала преобразовываем эту функцию к виду: . Сначала преобразовываем эту функцию к виду:  . Теперь производная вычисляется без труда: . Теперь производная вычисляется без труда: 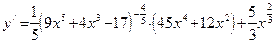 . .
2. Если нужно продифференцировать дробь, числитель которой – постоянное число, то перед дифференцированием знаменатель с показателем минус единица нужно поместить в числитель. Пусть, например, 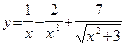 . Преобразовываем функцию следующим образом: . Преобразовываем функцию следующим образом: 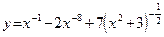 . Теперь . Теперь 
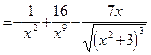 . .
3. При дифференцировании не следует путать производные степенной и показательной функций. Для примера рассмотрим функции  и и 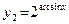 . У функции . У функции  первая операция есть функция арксинус, а вторая операция – степенная функция (возведение в степень с постоянным показателем 2). Поэтому, следуя правилу дифференцирования сложной функции, получим первая операция есть функция арксинус, а вторая операция – степенная функция (возведение в степень с постоянным показателем 2). Поэтому, следуя правилу дифференцирования сложной функции, получим  . У второй функции первая операция также есть функция арксинус, но вторая операция – это взятие постоянного числа 2 с показателем . У второй функции первая операция также есть функция арксинус, но вторая операция – это взятие постоянного числа 2 с показателем  , то есть показательная функция. Поэтому , то есть показательная функция. Поэтому 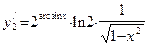 . .
4. Если нужно продифференцировать логарифмическую функцию, внутри которой содержится степень, то, применяя свойства логарифма, показатель степени следует вынести за знак логарифма. Пусть, например,  . Заменив радикал дробной степенью и вынеся показатель за знак логарифма, получим: . Заменив радикал дробной степенью и вынеся показатель за знак логарифма, получим: 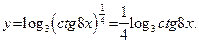 Поэтому Поэтому 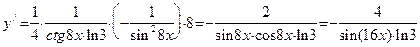 . .
5. Если внутрь какой-либо функции вставлено произведение или частное двух функций, то в этом случае не следует пытаться одним махом вычислить производную данной сложной функции, а лучше действовать поэтапно. Например, если  , то ее производную следует вычислять следующим образом: , то ее производную следует вычислять следующим образом: 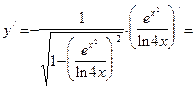
 . .
Логарифмическое дифференцирование
Рассмотрим метод нахождения производной степенно-показательной функции 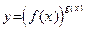 , у которой переменная x находится как в основании степени, так и в показателе. Прологарифмируем данную функцию: , у которой переменная x находится как в основании степени, так и в показателе. Прологарифмируем данную функцию: 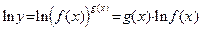 . Теперь продифференцируем обе части полученного равенства: . Теперь продифференцируем обе части полученного равенства: 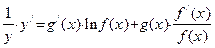 . Отсюда . Отсюда  . .
Пример 1. Найдем производную функции  . Применим метод логарифмического дифференцирования. Прологарифмируем данную функцию: . Применим метод логарифмического дифференцирования. Прологарифмируем данную функцию: 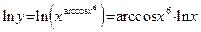 . Теперь найдем производные обеих частей полученного равенства: . Теперь найдем производные обеих частей полученного равенства: 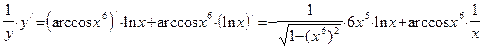 . В результате получаем: . В результате получаем: 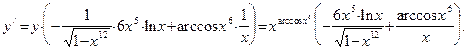
ТЕОРИЯ ПРЕДЕЛОВ
Лекция 2
Определение предела последовательности
Обозначим через N множество натуральных чисел. Итак, N=  . .
Определение 2. Последовательностью действительных чисел 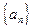 называется закон, согласно которому каждому называется закон, согласно которому каждому 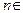 N ставится в соответствие действительное число N ставится в соответствие действительное число  , называемое элементом последовательности. Элемент , называемое элементом последовательности. Элемент  называется общим членом последовательности. называется общим членом последовательности.
Последовательность чаще всего задается своим общим членом  . Более подробно последовательность . Более подробно последовательность 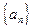 выписывают так: выписывают так: 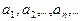 . .
Пример 2. 1) Расположим элементы последовательности с общим членом  на действительной прямой: на действительной прямой:

Мы видим, что элементы этой последовательности с ростом n приближаются к точке 0 на сколь угодно малое расстояние. Говорят также, что последовательность 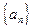 "сгущается" около точки 0, или "стремится" к точке 0. Мы увидим, что в соответствие с точным определением, которое будет дано чуть позже, число 0 является пределом последовательности "сгущается" около точки 0, или "стремится" к точке 0. Мы увидим, что в соответствие с точным определением, которое будет дано чуть позже, число 0 является пределом последовательности 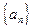 . .
2) Рассмотрим теперь следующую последовательность: 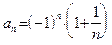 . Имеем: . Имеем: 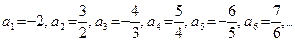 . Нанесем эти элементы на числовую прямую: . Нанесем эти элементы на числовую прямую:
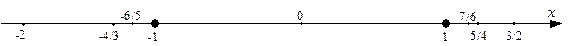
Нечетные элементы этой последовательности сгущаются вокруг точки –1, а четные – вокруг точки 1. То есть не существует одной такой точки, вокруг которой сгущались бы все члены данной последовательности с ростом n. О такого сорта последовательностях говорят, что они не имеют предела (расходятся).
3) Члены последовательности  с ростом n уходят все дальше и дальше вправо на числовой прямой: с ростом n уходят все дальше и дальше вправо на числовой прямой:

О такой последовательности мы будем говорить, что ее предел равен 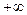 , или что она расходится к , или что она расходится к  . Аналогично, о последовательности . Аналогично, о последовательности 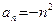 , члены которой с ростом n уходят все дальше и дальше влево на числовой прямой, говорят, что ее предел равен , члены которой с ростом n уходят все дальше и дальше влево на числовой прямой, говорят, что ее предел равен  , или что она расходится к , или что она расходится к  . .
4) Члены последовательности 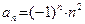 , перескакивая с одной стороны оси Ox на другую, с ростом n также удаляются на все большее и большее расстояние от начала координат: , перескакивая с одной стороны оси Ox на другую, с ростом n также удаляются на все большее и большее расстояние от начала координат:
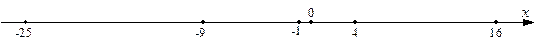
Так как элементы  не сохраняют определенный знак, то в этом случае будем говорить, что предел данной последовательности равен не сохраняют определенный знак, то в этом случае будем говорить, что предел данной последовательности равен 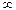 (то есть перед символом (то есть перед символом 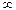 не будем ставить никакой знак). не будем ставить никакой знак).
Перед тем, как перейти к строгим определениям, напомним обозначения двух логических символов, с помощью которых сокращают некоторые записи. А именно, вместо фраз "для любого", "для всякого", "для каждого" часто записывают символ 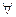 ; вместо слов "существует", "существуют" записывают символ ; вместо слов "существует", "существуют" записывают символ  . Кроме того, греческими буквами . Кроме того, греческими буквами 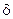 и и  мы будем всегда обозначать положительные переменные, могущие принимать сколь угодно малые значения. мы будем всегда обозначать положительные переменные, могущие принимать сколь угодно малые значения.
Определение 3. 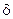 - окрестностью точки - окрестностью точки  называется множество точек называется множество точек 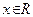 , удовлетворяющих неравенству , удовлетворяющих неравенству 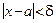 (которое, как известно, равносильно двойному неравенству (которое, как известно, равносильно двойному неравенству 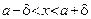 ). ).
Геометрически 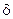 - окрестность точки - окрестность точки  представляет собой открытый интервал представляет собой открытый интервал 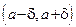 числовой прямой: числовой прямой:
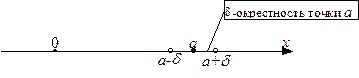
Определение 4. 1) Число  называется пределом последовательности называется пределом последовательности  , если , если 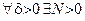 (N – натуральное число), такое, что (N – натуральное число), такое, что 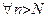 число число  попадает в попадает в 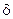 - окрестность точки a, то есть выполняется неравенство: - окрестность точки a, то есть выполняется неравенство:
|
| 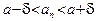 . .
| (2)
| Тот факт, что a есть предел 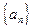 обозначается следующим образом: обозначается следующим образом:  . .
2) В случае, если не существует числа  , удовлетворяющего пункту 1) данного определения, говорят что последовательность , удовлетворяющего пункту 1) данного определения, говорят что последовательность 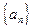 расходится (не имеет конечного предела). расходится (не имеет конечного предела).
3) Если 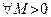 (M – сколь угодно большое число) (M – сколь угодно большое число) 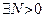 , такое, что , такое, что 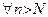 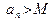 (соответственно, (соответственно, 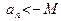 ), то говорят, что последовательность ), то говорят, что последовательность 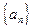 расходится к расходится к  (соответственно, расходится к (соответственно, расходится к  ), и этот факт обозначают следующим образом: ), и этот факт обозначают следующим образом:  (соответственно, (соответственно, 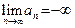 ). ).
4) Если 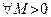 (M – сколь угодно большое число) (M – сколь угодно большое число) 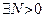 , такое, что , такое, что 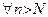 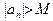 , то говорят, что последовательность , то говорят, что последовательность 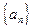 расходится к расходится к 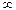 , и этот факт обозначают следующим образом: , и этот факт обозначают следующим образом: 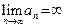 . .
Читателю предлагается доказать, что последовательности, взятые из пунктов 1)–4) примера 2, соответственно удовлетворяют пунктам 1)–4) определения 4, то есть, что 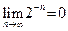 , , 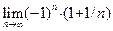 не существует, не существует, 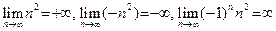 . .
Свойства предела последовательности
1. Предел константы равен самой этой константе, то есть если 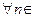 N N  , то , то
|
|  . .
|
| 2. Предел суммы двух последовательностей равен сумме пределов этих последовательностей, то есть если 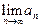 и и 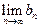 существуют, то существуют, то
3. Постоянный множитель можно вынести за знак предела, то есть если 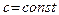 и и 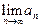 существует, то существует, то
|
| 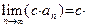 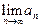 . .
|
| 4. Предел произведения двух последовательностей равен произведению пределов этих последовательностей, то есть если 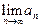 и и 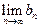 существуют, то существуют, то
|
|  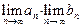 . .
|
| 5. Предел частного двух последовательностей равен частному пределов этих последовательностей, то есть если 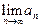 и и 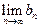 существуют и существуют и 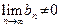 , то , то
|
|  . .
|
| 6. Если члены одной последовательности не превышают соответствующих членов другой последовательности, то и предел первой последовательности не превышает предела второй последовательности, то есть если 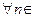 N N  и пределы и пределы 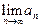 и и 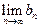 существуют, то существуют, то
|
| 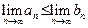 . .
|
| Заметим, что если выполняется строгое неравенство 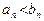 , то после перехода к пределу может получится равенство. Например, если , то после перехода к пределу может получится равенство. Например, если 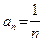 , а , а 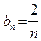 , то , то 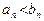 , однако , однако 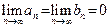 . Таким образом, в общем случае следствием неравенства . Таким образом, в общем случае следствием неравенства 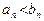 является нестрогое неравенство является нестрогое неравенство 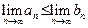 . .
7. Если 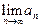 = = 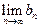 =a и =a и 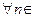 N N 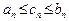 , то предел последовательности , то предел последовательности 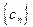 существует и существует и
|
| 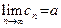 . .
|
| 8. Если последовательность 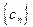 ограничена (то есть ограничена (то есть 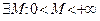 , такое, что , такое, что 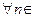 N N 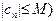 , а , а 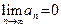 , то , то
|
| 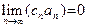 . .
|
| Доказательства свойств 1–6 мы опускаем. Их можно найти в любом учебнике по математическому анализу. Докажем лишь свойства 7 и 8.
Доказательство свойства 7. Пользуясь определением 4, распишем тот факт, что  : :  . Точно то же сделаем для . Точно то же сделаем для  : : 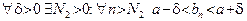 . Положим . Положим 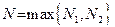 . Тогда при . Тогда при  два полученные двойные неравенства выполняются одновременно и, следовательно, имеем: два полученные двойные неравенства выполняются одновременно и, следовательно, имеем:
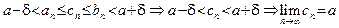 . ˆ . ˆ
Доказательство свойства 8. Прежде всего отметим, что равенство 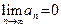 равносильно равенству равносильно равенству 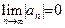 . Имеем: . Имеем:  . Так как . Так как 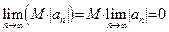 , то по свойству 7 , то по свойству 7  . .
Монотонные последовательности
Определение 5. Последовательность 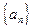 называется монотонно возрастающей (соответственно, монотонно убывающей), если называется монотонно возрастающей (соответственно, монотонно убывающей), если 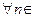 N N  (соответственно, (соответственно, 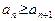 ). Если ). Если 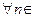 N выполняются соответствующие строгие неравенства, то говорят о строгом возрастании и строгом убывании последовательности. N выполняются соответствующие строгие неравенства, то говорят о строгом возрастании и строгом убывании последовательности.
Например, в примере 2 последовательность 1) строго монотонно убывает, последовательность  из пункта 3) строго монотонно возрастает, а последовательность 2) не является монотонной. Для монотонных последовательностей справедлива следующая теорема, доказательство которой выходит за рамки нашей программы. из пункта 3) строго монотонно возрастает, а последовательность 2) не является монотонной. Для монотонных последовательностей справедлива следующая теорема, доказательство которой выходит за рамки нашей программы.
Теорема 1. 1) Если последовательность 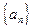 монотонно возрастает и ограничена сверху (то есть монотонно возрастает и ограничена сверху (то есть 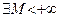 , такое, что , такое, что 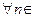 N N  , то данная последовательность имеет предел, причем , то данная последовательность имеет предел, причем 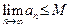 . .
2) Если последовательность 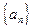 монотонно убывает и ограничена снизу (то есть монотонно убывает и ограничена снизу (то есть 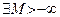 , такое, что , такое, что 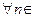 N N 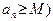 , то данная последовательность имеет предел, причем , то данная последовательность имеет предел, причем  . € . €
Пример 3. Рассмотрим последовательность  . Используя формулу бинома Ньютона и формулу суммы геометрической прогрессии, можно доказать (доказательство не слишком простое), что эта последовательность монотонно возрастает и ограничена сверху числом M=3. По теореме 1 данная последовательность имеет предел, который, следуя Л.Эйлеру, обозначают буквой e. Приближенное значение числа e таково: . Используя формулу бинома Ньютона и формулу суммы геометрической прогрессии, можно доказать (доказательство не слишком простое), что эта последовательность монотонно возрастает и ограничена сверху числом M=3. По теореме 1 данная последовательность имеет предел, который, следуя Л.Эйлеру, обозначают буквой e. Приближенное значение числа e таково: 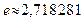 . .
Определение 6. Число
|
| 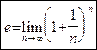 . .
|
(3)
| называется числом Эйлера. €
При изучении понятия предела функции нам понадобится следующее
Определение 7. Говорят, что последовательность 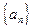 строго стремится к числу строго стремится к числу  , если , если  и и 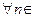 N выполняется неравенство N выполняется неравенство 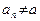 . € . €
Например, последовательность  из пункта 1) примера 2 стремится к нулю строго. Предел же последовательности из пункта 1) примера 2 стремится к нулю строго. Предел же последовательности 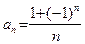 , как это следует из свойства 8 пределов последовательностей, равен нулю. Однако , как это следует из свойства 8 пределов последовательностей, равен нулю. Однако 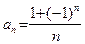 не стремится к нулю строго, так как при нечетных n не стремится к нулю строго, так как при нечетных n  . .
ТЕОРИЯ ПРЕДЕЛОВ
Лекция 3
Определение предела функции
Рассмотрим теперь действительную функцию  действительной переменной x с областью определения D(y), и пусть b – либо действительное число, либо бесконечно удаленная точка (то есть действительной переменной x с областью определения D(y), и пусть b – либо действительное число, либо бесконечно удаленная точка (то есть 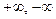 или просто или просто 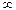 ). ).
Определение 8. 1) Предположим, что существует хотя бы одна последовательность  D(y), строго стремящаяся к a. Точка b называется пределом функции D(y), строго стремящаяся к a. Точка b называется пределом функции  при x стремящемся к a, если для любой последовательности при x стремящемся к a, если для любой последовательности  D(y), строго стремящейся к a, выполняется соотношение: D(y), строго стремящейся к a, выполняется соотношение: 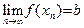 . Тот факт, что b является пределом функции . Тот факт, что b является пределом функции  при х стремящемся к a, обозначают так: при х стремящемся к a, обозначают так: 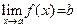 . .
2) Предположим, что существует хотя бы одна последовательность  D(y), строго монотонно возрастающая (соответственно, строго монотонно убывающая) к a. Точка b называется левым (соответственно правым) пределом функции D(y), строго монотонно возрастающая (соответственно, строго монотонно убывающая) к a. Точка b называется левым (соответственно правым) пределом функции  при x стремящемся к a, если для любой последовательности при x стремящемся к a, если для любой последовательности  D(y), строго монотонно возрастающей (соответственно, строго монотонно убывающей) к a, выполняется соотношение: D(y), строго монотонно возрастающей (соответственно, строго монотонно убывающей) к a, выполняется соотношение: 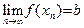 . Обозначение левого предела: . Обозначение левого предела: 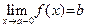 (соответственно, правого предела: (соответственно, правого предела: 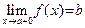 ). Ÿ ). Ÿ
Отметим, что из определения 8 сразу вытекает, что если предел (левый предел, правый предел) функции существует, то этот предел единственен.
Пример 4. Рассмотрим функцию
|
|  . .
|
| Ее график имеет вид:
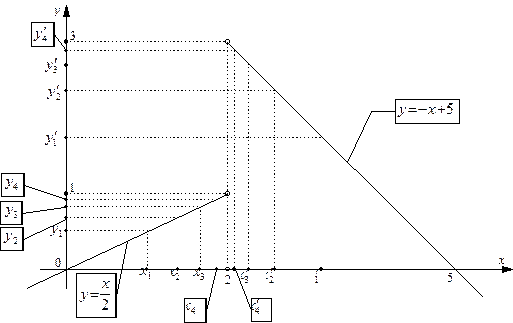
Заметим, что данная функция не определена в точке 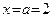 . Однако этот факт не влияет на вычисление предела (левого предела, правого предела) функции при стремлении x к этой точке, так как последовательность . Однако этот факт не влияет на вычисление предела (левого предела, правого предела) функции при стремлении x к этой точке, так как последовательность 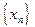 , фигурирующая в определении 8, не посещает предельную точку , фигурирующая в определении 8, не посещает предельную точку 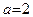 . .
Рассмотрим сначала последовательность 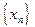 , строго монотонно возрастающую к , строго монотонно возрастающую к 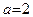 , и обозначим , и обозначим 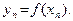 Так как Так как 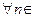 N N  , то, используя вид нашей функции, получаем: , то, используя вид нашей функции, получаем: 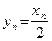 . Из рисунка видно, что при . Из рисунка видно, что при  последовательность последовательность  . Это также можно вычислить аналитически, используя свойства предела последовательности (которые верны также для левых и правых пределов): . Это также можно вычислить аналитически, используя свойства предела последовательности (которые верны также для левых и правых пределов):  . Это означает, что . Это означает, что  . .
Рассмотрим теперь последовательность 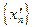 , строго монотонно убывающую к , строго монотонно убывающую к 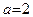 , и обозначим , и обозначим 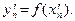 Так как Так как 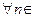 N N 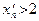 , то, используя вид нашей функции, получаем: , то, используя вид нашей функции, получаем: 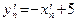 . Опять из рисунка видно, что при . Опять из рисунка видно, что при  последовательность последовательность  . Это же можно вычислить аналитически: . Это же можно вычислить аналитически:  . Это означает, что . Это означает, что  . .
Ясно, что 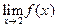 не существует. Действительно, рассмотрим последовательность не существует. Действительно, рассмотрим последовательность  , которая, очевидно, строго стремится к точке , которая, очевидно, строго стремится к точке 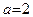 . Однако для последовательности соответствующих значений функции . Однако для последовательности соответствующих значений функции  , то есть для последовательности , то есть для последовательности  , получаем приблизительно такую же ситуацию, какую мы имели в пункте 2) примера 2. Поэтому эта последовательность расходится и, согласно пункту 1) определения 8, получаем, что , получаем приблизительно такую же ситуацию, какую мы имели в пункте 2) примера 2. Поэтому эта последовательность расходится и, согласно пункту 1) определения 8, получаем, что 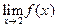 не существует. Читателю предлагается скрупулезно произвести все необходимые рассуждения. не существует. Читателю предлагается скрупулезно произвести все необходимые рассуждения.
Пример 5. Переместим параллельно самой себе правую ветвь графика из примера 4 на 2 единицы вниз. Получим следующий график:

Это график функции:
|
| 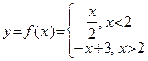 . .
|
| Рассуждая так же, как в примере 4, легко получить, что  , , 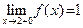 , и предел функции при , и предел функции при 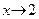 существует и равен 1, то есть существует и равен 1, то есть 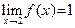 . .
Примеры 4 и 5 побуждают нас сформулировать следующую теорему, доказательство которой мы опускаем.
Теорема 2. Если 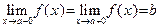 , то , то 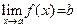 . .
Читателю предлагается подумать, как можно сформулировать обратную теорему.
Пример 6. Рассмотрим функцию 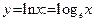 , где e – натуральное число (см. определение 6). Из школьного курса математики известно, что D(y)= , где e – натуральное число (см. определение 6). Из школьного курса математики известно, что D(y)=  . Рассмотрим точку . Рассмотрим точку  . Очевидно, что не существует последовательности . Очевидно, что не существует последовательности  D(y), стремящейся к D(y), стремящейся к  . Поэтому бессмысленно говорить о пределе функции . Поэтому бессмысленно говорить о пределе функции  при при 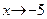 (именно поэтому в определении 8 требуется существование хотя бы одной последовательности (именно поэтому в определении 8 требуется существование хотя бы одной последовательности  D(y), строго стремящейся к предельной точке a). D(y), строго стремящейся к предельной точке a).
Пусть теперь  . Ясно, что не существует последовательности . Ясно, что не существует последовательности  D(y), строго монотонно возрастающей к D(y), строго монотонно возрастающей к 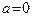 (то есть о левом пределе говорить бессмысленно). Однако существуют последовательности (то есть о левом пределе говорить бессмысленно). Однако существуют последовательности  D(y), строго монотонно убывающие к D(y), строго монотонно убывающие к 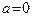 (например, можно взять (например, можно взять  ). Легко видеть (постройте график!), что для таких последовательностей ). Легко видеть (постройте график!), что для таких последовательностей 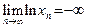 . Это означает, что . Это означает, что 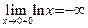 . Вместе с этим и . Вместе с этим и  . .
Свойства предела функции
Во всех нижеперечисленных свойствах, если речь идет о двух функциях  и и 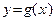 , то предполагается, что существует последовательность , то предполагается, что существует последовательность  D(f)ÇD(g), строго стремящаяся к a. D(f)ÇD(g), строго стремящаяся к a.
1. Предел константы равен самой этой константе, то есть если 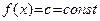 то то
|
| 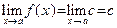 . .
|
| 2. Предел суммы двух функций равен сумме пределов этих функций, то есть если 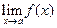 и и 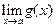 существуют и конечны, то существуют и конечны, то
3. Постоянный множитель можно вынести за знак предела, то есть если 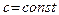 и и 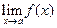 существует и конечен, то существует и конечен, то
|
| 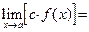 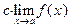 . .
|
| 4. Предел произведения двух функций равен произведению пределов этих функций, то есть если 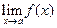 и и 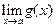 существуют и конечны, то существуют и конечны, то
|
|  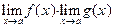 . .
|
| 5. Предел частного двух функций равен частному пределов этих функций, то есть если 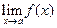 и и  существуют, конечны и существуют, конечны и  , то , то
|
| 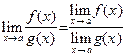 . .
|
| 6. Если в некоторой окрестности точки a (исключая, быть может, саму точку a) 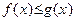 и пределы и пределы 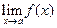 и и  существуют, то существуют, то
|
| 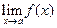 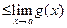 . .
|
| 7. Если 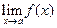 = =  =b и если в некоторой окрестности точки a (исключая, быть может, саму точку a) =b и если в некоторой окрестности точки a (исключая, быть может, саму точку a) 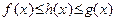 то предел функции то предел функции 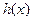 существует и существует и
|
| 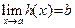 . .
|
| 8. Если в некоторой окрестности точки a (исключая, быть может, саму точку a) функция  ограничена (то есть ограничена (то есть 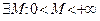 , такое, что в этой окрестности , такое, что в этой окрестности 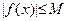 ), а ), а  , то , то
|
|  . .
|
| Доказательства всех этих свойств немедленно следуют из определения 8 и соответствующих свойств предела последовательности.
Замечательные пределы
1.  (первый замечательный предел). (первый замечательный предел).
Доказательство. Прежде всего покажем, что при 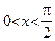 выполняется неравенство: выполняется неравенство:
|
| 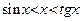
| (4)
| Обозначим площадь сектора AOB построенного единичного круга через S. Тогда  . Имеем: . Имеем: 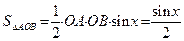 , ,  , , 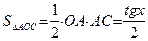 . Отсюда получаем выполнение (4). Поделив неравенство (4) на . Отсюда получаем выполнение (4). Поделив неравенство (4) на 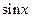 , получим: , получим: 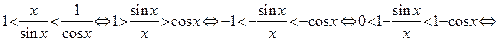 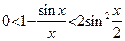 . Применяя в последнем неравенстве левую часть неравенства (4), получаем неравенство: . Применяя в последнем неравенстве левую часть неравенства (4), получаем неравенство:  . В силу четности функций . В силу четности функций  и и 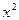 последнее двойное неравенство справедливо не только при последнее двойное неравенство справедливо не только при 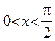 , но и при , но и при  . Так как . Так как  , то по свойству 7 предела функции имеем: , то по свойству 7 предела функции имеем:  , откуда немедленно следует равенство , откуда немедленно следует равенство  . œ . œ
2. 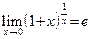 (второй замечательный предел). (второй замечательный предел).
Доказательство опускается (см. пример 3 и определение 6). œ
ТЕОРИЯ ПРЕДЕЛОВ
Лекция 4
Непрерывные функции
Определение 9. Функция  называется непрерывной в точке называется непрерывной в точке 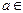 D(y), если D(y), если
|
| 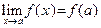 . .
| (5)
| Если равенство (5) не выполняется, то функция  называется разрывной в точке a. называется разрывной в точке a.
В примерах 4 и 5 рассматриваемые функции не были определены в точке 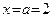 , поэтому не имеет смысла говорить о непрерывности этих функций в данной точке. , поэтому не имеет смысла говорить о непрерывности этих функций в данной точке.
Пример 7. Рассмотрим функцию из примера 5, но "доопределенную" в точке 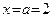 : :
|
|  . .
|
(6)
| График этой функции имеет вид:
Согласно определению 8, вычисляя предел функции при 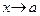 мы не используем значение функции в точке a. Поэтому предел, вычисленный нами в примере 5, сохраняет свое значение, то есть и в данном случае мы не используем значение функции в точке a. Поэтому предел, вычисленный нами в примере 5, сохраняет свое значение, то есть и в данном случае 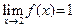 . Значение же функции в точке . Значение же функции в точке 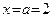 , согласно формуле (6), равно , согласно формуле (6), равно 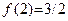 . Равенство (5) не выполняется, поэтому данная функция разрывна в точке . Равенство (5) не выполняется, поэтому данная функция разрывна в точке 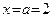 . Геометрически это выглядит как разрыв графика в исследуемой точке. . Геометрически это выглядит как разрыв графика в исследуемой точке.
Пример 8. Изменим значение функции из примера 7 только в одной точке, положив 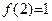 . График полученной функции имеет вид: . График полученной функции имеет вид:
Переопределением функции в точке 
Поиск по сайту:
|

 определена на открытом интервале
определена на открытом интервале 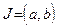 действительной прямой R, точка
действительной прямой R, точка 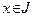 и число
и число 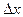 (называемое приращением независимой переменной x) таково, что
(называемое приращением независимой переменной x) таково, что 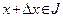 . При этом выражение
. При этом выражение 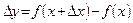 называют приращением данной функции в точке
называют приращением данной функции в точке 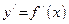 функции
функции  .
.
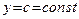 , то
, то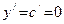 .
.
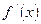 и
и 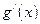 существуют, то
существуют, то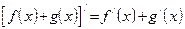 .
.
 , а
, а 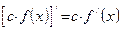 .
.
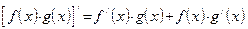 .
.
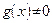 , то
, то .
.
 , где в свою очередь
, где в свою очередь  , и если
, и если 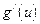 существуют, то
существуют, то .
.
 (где
(где  )
)
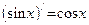
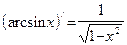
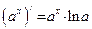 (где
(где 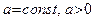 )
)


 (где
(где 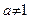 )
)
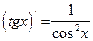
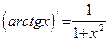

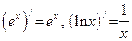 (частные случаи предыдущих двух формул при
(частные случаи предыдущих двух формул при  , где e – натуральное число)
, где e – натуральное число)

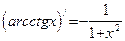
 и
и 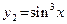 . Эти функции очень похожи. Для правильного их дифференцирования нужно отчетливо выделить операции, которые производятся над переменной x в данных математических выражениях. У первой функции переменная x сначала возводится в куб, а затем на полученный результат действует функция синус. Таким образом,
. Эти функции очень похожи. Для правильного их дифференцирования нужно отчетливо выделить операции, которые производятся над переменной x в данных математических выражениях. У первой функции переменная x сначала возводится в куб, а затем на полученный результат действует функция синус. Таким образом,  . Наоборот, у второй функции переменная x сначала подвергается действию функции синус, а затем результат возводится в куб, то есть
. Наоборот, у второй функции переменная x сначала подвергается действию функции синус, а затем результат возводится в куб, то есть 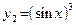 . Найдем производные этих функций, применяя цепное правило и таблицу производных. Заметим, что начинать дифференцирование нужно с последней операции, затем дифференцируют предпоследнюю операцию и, действуя таким образом, заканчивают производной первой операции.
. Найдем производные этих функций, применяя цепное правило и таблицу производных. Заметим, что начинать дифференцирование нужно с последней операции, затем дифференцируют предпоследнюю операцию и, действуя таким образом, заканчивают производной первой операции.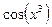 . При этом у полученной нами функции сохранился аргумент, которым обладал синус. Предпоследней операцией у рассматриваемой функции является возведение в куб (эта операция в данном примере одновременно является первой). Поэтому второе (и заключительное) звено цепного правила будет производная степенной функции
. При этом у полученной нами функции сохранился аргумент, которым обладал синус. Предпоследней операцией у рассматриваемой функции является возведение в куб (эта операция в данном примере одновременно является первой). Поэтому второе (и заключительное) звено цепного правила будет производная степенной функции 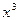 , то есть функция
, то есть функция  . Руководствуясь формулой 6 правил дифференцирования, окончательно получаем :
. Руководствуясь формулой 6 правил дифференцирования, окончательно получаем : 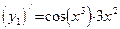 .
. . Отметим, что так как у исходной функции аргументом, который возводился в куб, был
. Отметим, что так как у исходной функции аргументом, который возводился в куб, был 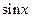 , то этот аргумент сохранился и в первом звене дифференцирования. Предпоследней (и одновременно первой) операцией рассматриваемой функции является синус, поэтому второе звено будет равно
, то этот аргумент сохранился и в первом звене дифференцирования. Предпоследней (и одновременно первой) операцией рассматриваемой функции является синус, поэтому второе звено будет равно  . Окончательно получаем:
. Окончательно получаем:  .
.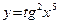 . Вычленим составляющие эту функцию простые операции:
. Вычленим составляющие эту функцию простые операции: 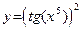 . Здесь первая операция – возведение переменной x в пятую степень, вторая операция – взятие тангенса от полученного результата и, наконец, последняя операция – возведение всего, что получилось, в квадрат. При дифференцировании цепное правило даст три звена. Первое звено получим, дифференцируя последнюю операцию. Оно будет состоять из функции
. Здесь первая операция – возведение переменной x в пятую степень, вторая операция – взятие тангенса от полученного результата и, наконец, последняя операция – возведение всего, что получилось, в квадрат. При дифференцировании цепное правило даст три звена. Первое звено получим, дифференцируя последнюю операцию. Оно будет состоять из функции  . Второе звено – производная предпоследней операции – равно
. Второе звено – производная предпоследней операции – равно 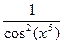 . И, наконец, последнее звено есть функция
. И, наконец, последнее звено есть функция  . В результате имеем:
. В результате имеем: 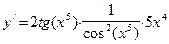 .
.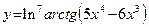 . Здесь первой операцией целесообразно считать многочлен
. Здесь первой операцией целесообразно считать многочлен 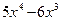 . Вторая операция – это взятие арктангенса от многочлена, третья операция – вычисление натурального логарифма, четвертая операция – возведение всего полученного в седьмую степень. Применяя цепное правило, получаем:
. Вторая операция – это взятие арктангенса от многочлена, третья операция – вычисление натурального логарифма, четвертая операция – возведение всего полученного в седьмую степень. Применяя цепное правило, получаем: 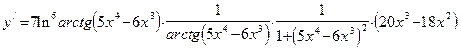 .
.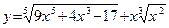 . Сначала преобразовываем эту функцию к виду:
. Сначала преобразовываем эту функцию к виду:  . Теперь производная вычисляется без труда:
. Теперь производная вычисляется без труда: 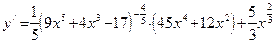 .
.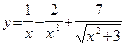 . Преобразовываем функцию следующим образом:
. Преобразовываем функцию следующим образом: 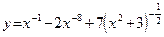 . Теперь
. Теперь 
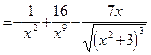 .
. и
и 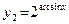 . У функции
. У функции  первая операция есть функция арксинус, а вторая операция – степенная функция (возведение в степень с постоянным показателем 2). Поэтому, следуя правилу дифференцирования сложной функции, получим
первая операция есть функция арксинус, а вторая операция – степенная функция (возведение в степень с постоянным показателем 2). Поэтому, следуя правилу дифференцирования сложной функции, получим  . У второй функции первая операция также есть функция арксинус, но вторая операция – это взятие постоянного числа 2 с показателем
. У второй функции первая операция также есть функция арксинус, но вторая операция – это взятие постоянного числа 2 с показателем  , то есть показательная функция. Поэтому
, то есть показательная функция. Поэтому 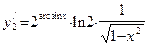 .
. . Заменив радикал дробной степенью и вынеся показатель за знак логарифма, получим:
. Заменив радикал дробной степенью и вынеся показатель за знак логарифма, получим: 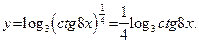 Поэтому
Поэтому 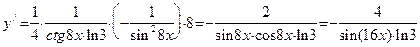 .
. , то ее производную следует вычислять следующим образом:
, то ее производную следует вычислять следующим образом: 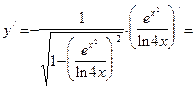
 .
.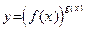 , у которой переменная x находится как в основании степени, так и в показателе. Прологарифмируем данную функцию:
, у которой переменная x находится как в основании степени, так и в показателе. Прологарифмируем данную функцию: 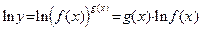 . Теперь продифференцируем обе части полученного равенства:
. Теперь продифференцируем обе части полученного равенства: 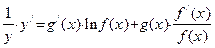 . Отсюда
. Отсюда  .
. . Применим метод логарифмического дифференцирования. Прологарифмируем данную функцию:
. Применим метод логарифмического дифференцирования. Прологарифмируем данную функцию: 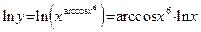 . Теперь найдем производные обеих частей полученного равенства:
. Теперь найдем производные обеих частей полученного равенства: 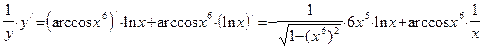 . В результате получаем:
. В результате получаем: 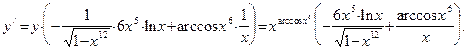
 .
.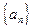 называется закон, согласно которому каждому
называется закон, согласно которому каждому  N ставится в соответствие действительное число
N ставится в соответствие действительное число  , называемое элементом последовательности. Элемент
, называемое элементом последовательности. Элемент 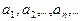 .
. на действительной прямой:
на действительной прямой:
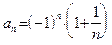 . Имеем:
. Имеем: 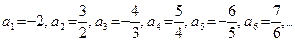 . Нанесем эти элементы на числовую прямую:
. Нанесем эти элементы на числовую прямую: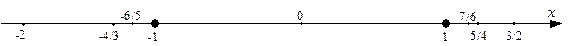
 с ростом n уходят все дальше и дальше вправо на числовой прямой:
с ростом n уходят все дальше и дальше вправо на числовой прямой:
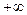 , или что она расходится к
, или что она расходится к  . Аналогично, о последовательности
. Аналогично, о последовательности 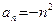 , члены которой с ростом n уходят все дальше и дальше влево на числовой прямой, говорят, что ее предел равен
, члены которой с ростом n уходят все дальше и дальше влево на числовой прямой, говорят, что ее предел равен  , или что она расходится к
, или что она расходится к 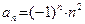 , перескакивая с одной стороны оси Ox на другую, с ростом n также удаляются на все большее и большее расстояние от начала координат:
, перескакивая с одной стороны оси Ox на другую, с ростом n также удаляются на все большее и большее расстояние от начала координат: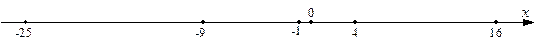
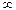 (то есть перед символом
(то есть перед символом 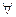 ; вместо слов "существует", "существуют" записывают символ
; вместо слов "существует", "существуют" записывают символ  . Кроме того, греческими буквами
. Кроме того, греческими буквами 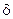 и
и  мы будем всегда обозначать положительные переменные, могущие принимать сколь угодно малые значения.
мы будем всегда обозначать положительные переменные, могущие принимать сколь угодно малые значения. называется множество точек
называется множество точек 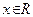 , удовлетворяющих неравенству
, удовлетворяющих неравенству 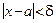 (которое, как известно, равносильно двойному неравенству
(которое, как известно, равносильно двойному неравенству 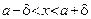 ).
).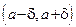 числовой прямой:
числовой прямой: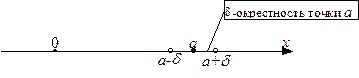
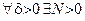 (N – натуральное число), такое, что
(N – натуральное число), такое, что 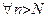 число
число 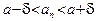 .
.
 .
.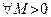 (M – сколь угодно большое число)
(M – сколь угодно большое число) 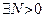 , такое, что
, такое, что 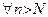
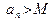 (соответственно,
(соответственно, 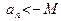 ), то говорят, что последовательность
), то говорят, что последовательность  (соответственно,
(соответственно, 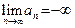 ).
).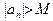 , то говорят, что последовательность
, то говорят, что последовательность 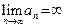 .
.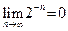 ,
, 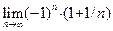 не существует,
не существует, 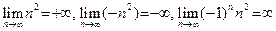 .
.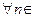 N
N  , то
, то .
.
 и
и 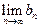 существуют, то
существуют, то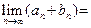
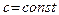 и
и 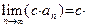

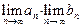 .
.
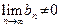 , то
, то .
.
 и пределы
и пределы 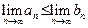 .
.
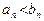 , то после перехода к пределу может получится равенство. Например, если
, то после перехода к пределу может получится равенство. Например, если 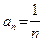 , а
, а 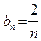 , то
, то 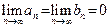 . Таким образом, в общем случае следствием неравенства
. Таким образом, в общем случае следствием неравенства 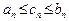 , то предел последовательности
, то предел последовательности 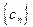 существует и
существует и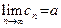 .
.
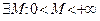 , такое, что
, такое, что 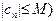 , а
, а 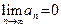 , то
, то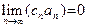 .
.
 :
:  . Точно то же сделаем для
. Точно то же сделаем для  :
: 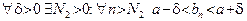 . Положим
. Положим 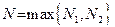 . Тогда при
. Тогда при  два полученные двойные неравенства выполняются одновременно и, следовательно, имеем:
два полученные двойные неравенства выполняются одновременно и, следовательно, имеем: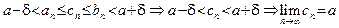 . ˆ
. ˆ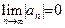 . Имеем:
. Имеем:  . Так как
. Так как 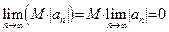 , то по свойству 7
, то по свойству 7  .
. (соответственно,
(соответственно, 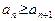 ). Если
). Если 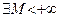 , такое, что
, такое, что  , то данная последовательность имеет предел, причем
, то данная последовательность имеет предел, причем 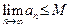 .
.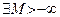 , такое, что
, такое, что 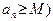 , то данная последовательность имеет предел, причем
, то данная последовательность имеет предел, причем  . €
. € . Используя формулу бинома Ньютона и формулу суммы геометрической прогрессии, можно доказать (доказательство не слишком простое), что эта последовательность монотонно возрастает и ограничена сверху числом M=3. По теореме 1 данная последовательность имеет предел, который, следуя Л.Эйлеру, обозначают буквой e. Приближенное значение числа e таково:
. Используя формулу бинома Ньютона и формулу суммы геометрической прогрессии, можно доказать (доказательство не слишком простое), что эта последовательность монотонно возрастает и ограничена сверху числом M=3. По теореме 1 данная последовательность имеет предел, который, следуя Л.Эйлеру, обозначают буквой e. Приближенное значение числа e таково: 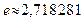 .
.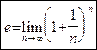 .
.
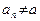 . €
. €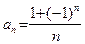 , как это следует из свойства 8 пределов последовательностей, равен нулю. Однако
, как это следует из свойства 8 пределов последовательностей, равен нулю. Однако  .
. действительной переменной x с областью определения D(y), и пусть b – либо действительное число, либо бесконечно удаленная точка (то есть
действительной переменной x с областью определения D(y), и пусть b – либо действительное число, либо бесконечно удаленная точка (то есть 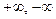 или просто
или просто  D(y), строго стремящаяся к a. Точка b называется пределом функции
D(y), строго стремящаяся к a. Точка b называется пределом функции 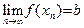 . Тот факт, что b является пределом функции
. Тот факт, что b является пределом функции 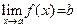 .
.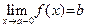 (соответственно, правого предела:
(соответственно, правого предела: 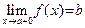 ). Ÿ
). Ÿ .
.
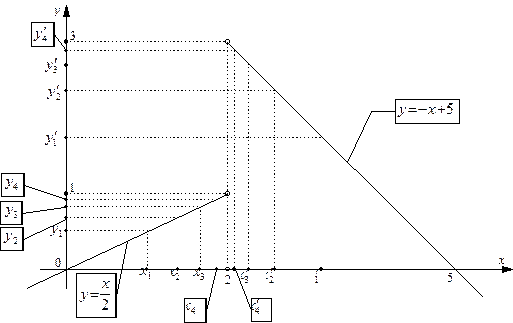
 . Однако этот факт не влияет на вычисление предела (левого предела, правого предела) функции при стремлении x к этой точке, так как последовательность
. Однако этот факт не влияет на вычисление предела (левого предела, правого предела) функции при стремлении x к этой точке, так как последовательность  , фигурирующая в определении 8, не посещает предельную точку
, фигурирующая в определении 8, не посещает предельную точку 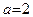 .
.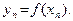 Так как
Так как  , то, используя вид нашей функции, получаем:
, то, используя вид нашей функции, получаем: 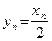 . Из рисунка видно, что при
. Из рисунка видно, что при  последовательность
последовательность  . Это также можно вычислить аналитически, используя свойства предела последовательности (которые верны также для левых и правых пределов):
. Это также можно вычислить аналитически, используя свойства предела последовательности (которые верны также для левых и правых пределов):  . Это означает, что
. Это означает, что  .
.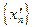 , строго монотонно убывающую к
, строго монотонно убывающую к 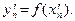 Так как
Так как 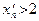 , то, используя вид нашей функции, получаем:
, то, используя вид нашей функции, получаем: 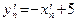 . Опять из рисунка видно, что при
. Опять из рисунка видно, что при  . Это же можно вычислить аналитически:
. Это же можно вычислить аналитически:  . Это означает, что
. Это означает, что  .
.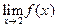 не существует. Действительно, рассмотрим последовательность
не существует. Действительно, рассмотрим последовательность  , которая, очевидно, строго стремится к точке
, которая, очевидно, строго стремится к точке  , получаем приблизительно такую же ситуацию, какую мы имели в пункте 2) примера 2. Поэтому эта последовательность расходится и, согласно пункту 1) определения 8, получаем, что
, получаем приблизительно такую же ситуацию, какую мы имели в пункте 2) примера 2. Поэтому эта последовательность расходится и, согласно пункту 1) определения 8, получаем, что 
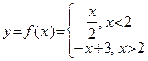 .
.
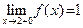 , и предел функции при
, и предел функции при 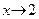 существует и равен 1, то есть
существует и равен 1, то есть 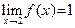 .
.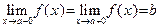 , то
, то 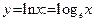 , где e – натуральное число (см. определение 6). Из школьного курса математики известно, что D(y)=
, где e – натуральное число (см. определение 6). Из школьного курса математики известно, что D(y)=  . Рассмотрим точку
. Рассмотрим точку  . Очевидно, что не существует последовательности
. Очевидно, что не существует последовательности  при
при 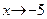 (именно поэтому в определении 8 требуется существование хотя бы одной последовательности
(именно поэтому в определении 8 требуется существование хотя бы одной последовательности  . Ясно, что не существует последовательности
. Ясно, что не существует последовательности 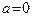 (то есть о левом пределе говорить бессмысленно). Однако существуют последовательности
(то есть о левом пределе говорить бессмысленно). Однако существуют последовательности  ). Легко видеть (постройте график!), что для таких последовательностей
). Легко видеть (постройте график!), что для таких последовательностей 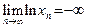 . Это означает, что
. Это означает, что 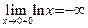 . Вместе с этим и
. Вместе с этим и  .
. , то предполагается, что существует последовательность
, то предполагается, что существует последовательность  то
то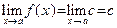 .
.
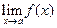 и
и 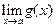 существуют и конечны, то
существуют и конечны, то =
= 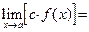
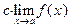 .
.

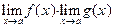 .
.
 существуют, конечны и
существуют, конечны и  , то
, то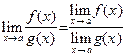 .
.
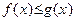 и пределы
и пределы 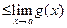 .
.
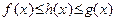 то предел функции
то предел функции 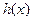 существует и
существует и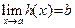 .
.
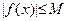 ), а
), а  , то
, то .
.
 (первый замечательный предел).
(первый замечательный предел).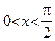 выполняется неравенство:
выполняется неравенство: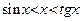

 . Имеем:
. Имеем: 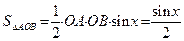 ,
,  ,
, 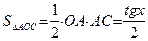 . Отсюда получаем выполнение (4). Поделив неравенство (4) на
. Отсюда получаем выполнение (4). Поделив неравенство (4) на 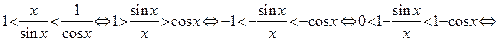
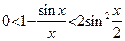 . Применяя в последнем неравенстве левую часть неравенства (4), получаем неравенство:
. Применяя в последнем неравенстве левую часть неравенства (4), получаем неравенство:  . В силу четности функций
. В силу четности функций  и
и 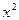 последнее двойное неравенство справедливо не только при
последнее двойное неравенство справедливо не только при  . Так как
. Так как  , то по свойству 7 предела функции имеем:
, то по свойству 7 предела функции имеем:  , откуда немедленно следует равенство
, откуда немедленно следует равенство 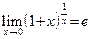 (второй замечательный предел).
(второй замечательный предел).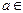 D(y), если
D(y), если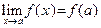 .
.
 .
.

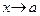 мы не используем значение функции в точке a. Поэтому предел, вычисленный нами в примере 5, сохраняет свое значение, то есть и в данном случае
мы не используем значение функции в точке a. Поэтому предел, вычисленный нами в примере 5, сохраняет свое значение, то есть и в данном случае 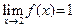 . Значение же функции в точке
. Значение же функции в точке 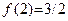 . Равенство (5) не выполняется, поэтому данная функция разрывна в точке
. Равенство (5) не выполняется, поэтому данная функция разрывна в точке 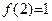 . График полученной функции имеет вид:
. График полученной функции имеет вид: