 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Связь бесконечно малой величины с бесконечно большой
Между бесконечно малой и бесконечно большой величинами существует обратная зависимость, а именно: если если
Понятие о пределе переменной величины Пусть переменная 5,1; 5,01; 5,001; 5,0001 … или 4,9; 4,99; 4,999; 4,9999 … Мы видим, что абсолютная величина разности Число 5 называется пределом переменной Определение: Постоянная Следовательно,
Свойства бесконечно малых величин 1) Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая
2) Произведение бесконечно малой величины
Следствие: Произведение ограниченной переменной на бесконечно малую величину есть величина бесконечно малая.
ТЕОРЕМЫ О ПРЕДЕЛАХ Теорема I. Переменная величина не может иметь двух различных пределов. Теорема II. Предел суммы конечного числа переменных величин, имеющих пределы, равен сумме пределов этих переменных величин. Доказательство: Докажем для двух переменных величин.
Сложив эти равенства, получим
Имеем в левой части разность между переменной Следовательно, согласно определению предела
Точно также можно доказать для трех, четырех и любого конечного числа переменных. Теорема III. Предел разности переменных, имеющих пределы, равен разности пределов этих переменных
Теорема IV. Предел произведения конечного числа переменных, имеющих пределы, равен произведению пределов этих переменных. Доказательство: Дано, что
Так как
то
Умножим эти равенства, получим
В левой части имеем разность между переменной Следовательно,
Эту теорему можно доказать для любого конечного числа переменных. Следствие 1: Следствие 2:
Теорема V. Предел частного от деления двух переменных величин, имеющих пределы, равен частному от деления пределов делимого и делителя при условии, что предел делителя не равен нулю
Предел функции О пределе функции можно говорить только при условии задания предела, к которому стремится ее аргумент Определение: Число
Иначе говоря, число
Поиск по сайту: |
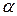 - бесконечно малая величина, не равная 0, то обратная ей величина
- бесконечно малая величина, не равная 0, то обратная ей величина 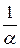 - бесконечно большая величина (
- бесконечно большая величина ( 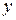 - бесконечно большая величина, то обратная
- бесконечно большая величина, то обратная 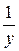 - бесконечно малая величина.
- бесконечно малая величина. , изменяясь неограниченно близко приближается к числу 5, принимая следующие значения
, изменяясь неограниченно близко приближается к числу 5, принимая следующие значения 5
5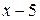 стремится к нулю, то есть
стремится к нулю, то есть  ; 0,01; 0,001; 0,0001
; 0,01; 0,001; 0,0001  - величина бесконечно малая.
- величина бесконечно малая. или
или 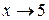 .
.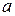 называется пределом переменной
называется пределом переменной 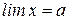 , если
, если 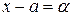 - бесконечно малая, можно записать, что
- бесконечно малая, можно записать, что 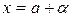 .
.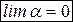 .
.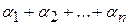 - бесконечно малая.
- бесконечно малая.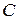 есть величина бесконечно малая
есть величина бесконечно малая бесконечно малая.
бесконечно малая. - переменные
- переменные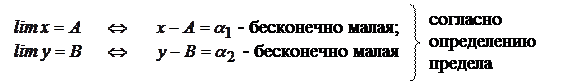
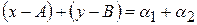 ,
,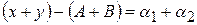 .
.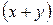 и постоянной
и постоянной 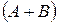 , в правой бесконечно малую.
, в правой бесконечно малую.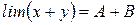 ,
, .
.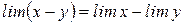 .
.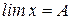 ,
, 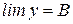 . Докажем теорему для двух переменных, то есть нужно доказать, что
. Докажем теорему для двух переменных, то есть нужно доказать, что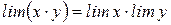 .
.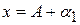 ,
,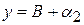 .
. ,
,

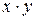 и постоянной
и постоянной  , в правой части сумму бесконечно малых величин (теорема о б/м).
, в правой части сумму бесконечно малых величин (теорема о б/м).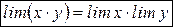 .
. , где
, где 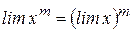 , где
, где 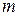 - любое действительное значение.
- любое действительное значение. .
. , если
, если 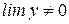 .
.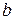 называется пределом функции
называется пределом функции 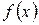 в точке
в точке  .
.

 - б/м при условии
- б/м при условии 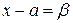 - б/м.
- б/м.