 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Бесконечно большая величинаСтр 1 из 3Следующая ⇒
Учреждение образования «ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ» кафедра математики и физики
КУРС ЛЕКЦИЙ
по дисциплине «ВЫСШАЯ МАТЕМАТИКА»
ТЕОРИЯ ПРЕДЕЛОВ
Витебск2006
Составитель Т.К. Гресюк
Издание утверждено на заседании кафедры М и Ф «20» марта 2006 г., протокол № 8
Зав. кафедрой Л.Л. Гладков
ТЕОРИЯ ПРЕДЕЛОВ Бесконечно малая величина Бесконечно большая величина Связь бесконечно малой величины с бесконечно большой Понятие о пределе переменной величины 5) Предел функции
Мы знаем, что в математике и ее приложениях встречаются величины постоянный и величины переменные. На числовой оси Закон изменения переменной величины можно задать последовательностью числовых значений, которые она принимает.
Бесконечно малая величина Возьмем переменную величину
или
По мере увеличения номера места, занимаемого числами этих последовательностей, абсолютная величина Пусть например В этом случае говорят, что величина Определение: Бесконечно малой величиной называется переменная величина
Это значит, что для любого сколь угодно малого
Бесконечно большая величина Пусть переменная величина
или - Мы видим, что абсолютная величина
Определение: Бесконечно большой величиной называется переменная
Если
Поиск по сайту: |
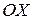 постоянной величине
постоянной величине 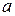 соответствует неподвижная точка
соответствует неподвижная точка  , а переменной величине
, а переменной величине  - движущаяся вправо или влево точка
- движущаяся вправо или влево точка  .
.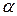 , принимающую последовательно значения:
, принимающую последовательно значения: ;
;  ;
;  ; …
; … 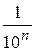 …
… ;
;  ;
; 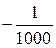 ; …
; …  …
… ни выбрали, в каждой из этих последовательностей найдется число, начиная с которого абсолютная величина значений
ни выбрали, в каждой из этих последовательностей найдется число, начиная с которого абсолютная величина значений  , то начиная с шестого члена, который равен
, то начиная с шестого члена, который равен  .
. . (1)
. (1) найдется
найдется  , что для всех
, что для всех 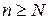 будет выполняться, что
будет выполняться, что  .
.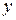 принимает последовательно значения:
принимает последовательно значения: ;
; 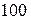 ;
;  ; …
; … 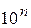 …
… , то есть, задав
, то есть, задав  ,
,  , мы найдем в заданной последовательности номер
, мы найдем в заданной последовательности номер  .
. .
.