 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Предел дробно-рациональной функцииСтр 1 из 2Следующая ⇒
Предел целой рациональной функции При вычислении предела целой рациональной функции можно в аналитическом выражении функции заменить аргумент его предельным значением (такое правило можно сформулировать, опираясь на теоремы о пределах и свойства бесконечно больших и малых величин). Пример. Найти Решение. Функция
Предел дробно-рациональной функции При вычислении предела дробно-рациональной функции можно в аналитическом выражении функции заменить аргумент его предельным значением, если при этом предельном значении знаменатель не обращается в нуль. (*) Пример. Найти Решение. Нужно вычислить предел дробно-рациональной функции. Проверим, не обращается ли в нуль знаменатель дроби при х=1: 12-2.1+4=3≠0; значит
Пример.Найти Решение. Проверяем знаменатель дроби при х=3: 32-5.3+6=0, т.е. функция И знаменатель, и числитель дроби при х=3 равны нулю. Мы имеем отношение двух бесконечно малых функций, о котором без специального исследования ничего определенного сказать нельзя (говорят, что имеем неопределенность вида Т.о. Итак, чтобы определить предел дробно-рациональной функции в случае, когда при х→хо числитель и знаменатель дроби имеют пределы, равные нулю, (т.е. неопределенность вида Пример. Вычислить Решение. Разделить числитель и знаменатель на одно и тоже не равное нулю выражение, значит сократить дробь. Для этого разложим числитель и знаменатель на множители, воспользовавшись формулой разложения на множители квадратного трехчлена ах2+вх+с=а(х-х1)(х-х2), где х1 и х2 –корни квадратного уравнения ах2+вх+с=0. х2-х-12=0, D=1+4·12=49, х2+5х+6=0, D=25-4.6=1,
Замечание. Деление многочлена на многочлен можно выполнять в столбик:
Т.е. х2-х-12=(х-4)(х+3); х2+5х+6=(х+2)(х+3). Пример.Вычислить Решение. В дальнейшем при вычислении пределов такого типа, можно сразу записывать ответ.
Поиск по сайту: |
 .
.
 - целая рациональная. Для вычисления ее предела в аналитическом выражении функции заменим
- целая рациональная. Для вычисления ее предела в аналитическом выражении функции заменим  его предельным значением. Подробное решение выглядит так:
его предельным значением. Подробное решение выглядит так: , но обычно оформляют запись следующим образом:
, но обычно оформляют запись следующим образом: 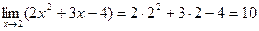 .
. .
. .
. .
. при х=3 не существует. Мы не можем применить ни теорему о пределе дроби, ни правило (*). Вспомним, что определение предела функции f(x) при х→хо не требует, чтобы точка х=хо входила в область определения функции. Поэтому значение х=хо можно не рассматривать. В данном примере мы будем считать, что х, стремясь к 3, никогда не становится равным 3, и поэтому значение функции
при х=3 не существует. Мы не можем применить ни теорему о пределе дроби, ни правило (*). Вспомним, что определение предела функции f(x) при х→хо не требует, чтобы точка х=хо входила в область определения функции. Поэтому значение х=хо можно не рассматривать. В данном примере мы будем считать, что х, стремясь к 3, никогда не становится равным 3, и поэтому значение функции 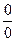 ). Разделим числитель и знаменатель дроби на х-3. Т.к. значение х=3 мы не рассматриваем, значит х-3≠0 и такое деление возможно. Сокращая дробь, получим
). Разделим числитель и знаменатель дроби на х-3. Т.к. значение х=3 мы не рассматриваем, значит х-3≠0 и такое деление возможно. Сокращая дробь, получим  . Заметим, что если не рассматривать значение х=3, полученная функция будет тождественна данной функции и можно находить ее предел вместо данной.
. Заметим, что если не рассматривать значение х=3, полученная функция будет тождественна данной функции и можно находить ее предел вместо данной. .
. ), надо и числитель и знаменатель дроби разделить на х-хо и перейти к пределу. Если и после этого определенность не исчезнет, нужно произвести повторное деление на х-хо. (В элементарной математике существует следствие из теоремы Безу, согласно которому, если многочлен обращается в нуль при х=хо, то он делится без остатка на х-хо. Поэтому такое деление возможно).
), надо и числитель и знаменатель дроби разделить на х-хо и перейти к пределу. Если и после этого определенность не исчезнет, нужно произвести повторное деление на х-хо. (В элементарной математике существует следствие из теоремы Безу, согласно которому, если многочлен обращается в нуль при х=хо, то он делится без остатка на х-хо. Поэтому такое деление возможно).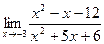 .
. ;
;
 значит х2-х-12=(х-4)(х+3);
значит х2-х-12=(х-4)(х+3);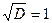 ;
;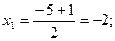
 значит х2+5х+6=(х+2)(х+3), тогда
значит х2+5х+6=(х+2)(х+3), тогда .
.
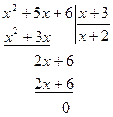
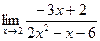 .
. , т.е. предел числителя при х→2 равен -4, а предел знаменателя равен нулю. Теорему о пределе дроби применить нельзя. Рассмотрим предел обратной дроби
, т.е. предел числителя при х→2 равен -4, а предел знаменателя равен нулю. Теорему о пределе дроби применить нельзя. Рассмотрим предел обратной дроби  (здесь теорема о пределе дроби применима, т.к. предел знаменателя -3х+2 не равен нулю). Т.к. предел функции
(здесь теорема о пределе дроби применима, т.к. предел знаменателя -3х+2 не равен нулю). Т.к. предел функции  равен нулю, то эта функция при х→2 бесконечно малая, значит обратная ей функция
равен нулю, то эта функция при х→2 бесконечно малая, значит обратная ей функция  при х→2 бесконечно большая, и тогда ее предел
при х→2 бесконечно большая, и тогда ее предел  (см. свойства бесконечно больших функций).
(см. свойства бесконечно больших функций).