 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
I. Функции двух переменных ⇐ ПредыдущаяСтр 2 из 2
Определение 1.1. Функцией двух переменных называется правило, по которому каждой паре значений (x, y) некоторой области D вещественной плоскости R2 ставится в соответствие единственное значение вещественной переменной z. При этом область D называется областью определения функции и обозначается D(z), а множество значений, которые пробегает z, когда пара (x, y) принимает все возможные значения из области D(z), называется областью значения функции z и обозначается E(z). Простейшим примером функции двух переменных может являться итоговая оценка по дисциплине «Высшая математика». Пусть x—количество баллов, набранных за семестр, y—количество баллов, набранных на экзамене, z—баллы дисциплины. Тогда имеет место функциональная зависимость z = (x+y)/2.Областью определения данной функции является Пример 1.1. Записать область определения функции и графически её изобразить. Решение. D(z): 1) 2-x-y2=0 или y2=-(x-2)—это уравнение параболы с вершиной в точке (2; 0) и ветвями влево. Поскольку неравенство строгое, ветви изображены пунктиром. Для выбора части плоскости, координаты точек которой удовлетворяют неравенству, воспользуемся методом пробной точки: возьмём точку М0(0, 0) (не лежащую на параболе) и подставим её координаты в ограничение 2) 3) Пересечение данных областей является графическим представлением D(z). Замечание. Отметим, что метод пробной точки является аналогом метода интервалов, применяемого для определения промежутков знакопостоянства функции одной переменной: вместо координатной прямой – координатная плоскость, вместо точек на прямой – линии на плоскости. Способы задания функции двух переменных: аналитический (с помощью формулы), табличный и графический ( с помощью графика или линий уровня). Определение 1.2. Функция Q=A капитала и L—труда. При фиксированных значениях
Определение 1.3. Графиком функции двух переменных z = f(x, y) называется множество точек M(x, y, f(x, y)) пространства R3, для которых (x, y) Определение 1.4. Линиями уровня функции z = f(x, y) называются кривые на плоскости Оxy, уравнения которых имеют вид f(x, y) = С, где С—постоянная, принадлежащая области значения функции z. Примерами линий уровня являются изотермы на синоптических картах и линии высоты на топографических. Пример 1.2. Описать линии уровня функции z = 1-x-y. Решение. Поскольку уравнение 1-x-y=C (С Пример 1.3. Описать линии уровня функции z = x2+y2-2y. Решение.Преобразуем выражение Пример 1.4. Объём продукции Q, производимой некоторой фирмой, определяется производственной функцией Q = 25K1/3L2/3, где К—объём вложенного капитала, L—трудовых ресурсов. Построить линию уровня, которая отвечает выпуску Q=50 единиц продукции. Дать экономическую интерпретацию полученных результатов. Решение. Из уравнения 25K1/3L2/3=50 находим Определение 1.5. Частным приращением функции Определение 1.6. Частной производной функции двух переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению этой переменной, когда последний стремится к нулю, если указанный предел существует
Пример 1.5. а)
б) в) Пример 1.6. Поток пассажиров z (за месяц) между двумя городами выражается функцией z= Решение. Определение 1.7. Производной функции по направлению, заданному вектором
которая показывает скорость изменения функции в данном направлении. Пример 1.7. Найти производную функции Решение. Поскольку
Вывод. Функция z в точке М0 по направлению вектора Определение 1.8. Градиентом функции z = f(x; y) в точке M(x0; y0) называется вектор, координатами которого являются значения частных производных в данной точке
Теорема 1.1. Вектор-градиент указывает направление наиболее быстрого возрастания функции. Пример 1.8. Для функции z = x0,5y0,5 найти направление из точки M(3; 4), в котором скорость возрастания функции максимальна. Решение. Поскольку Вывод. Функция z в точке М возрастает наиболее быстро в направлении Пример 1.9. Для некоторого предприятия производственная функция имеет вид Q=K0,5L0,5. В настоящий момент в основные фонды вложено 9 000 000 гривен, а в трудовые ресурсы— 1 000 000 гривен, и, следовательно, ежемесячно выпускается продукции на 300 000 гривен. У предприятия появились денежные средства в размере 1 000 000 гривен. Как их оптимально распределить, чтобы прирост выпуска продукции был максимальным. Решение. Данный пример является аналогом предыдущего, координаты точки М (9 000 000, 1 000 000).
находим Вывод. Оптимальным вариантом распределения денежных средств является инвестирование 100 180 гривен в основные фонды и 899 820 в трудовые ресурсы. Отметим, что данный результат практически очевиден: в производственную функцию факторы входят с одинаковым весом (0,5=0,5), а в наличии находятся в отношении 9:1; поэтому логично предположить, что вновь поступающие средства распределять надо в отношении приблизительно 1:9. Определение 1.9. Функции Пример 1.10. Найти частные производные второго порядка функции z=x3y2-xy3+5x-2y+3. Решение.
Как видим, смешанные производные совпадают. Возникает вопрос, это характерно только для данного примера или имеет место более общая закономерность. Ответ на этот вопрос даёт следующая Теорема Шварца. Если смешанные производные второго порядка существуют и непрерывны в точке М(x, y), то в этой точке их значения совпадают:
Определение 1.10. Точка M0(x0, y0) называется точкой локального максимума (минимума) функции z = f(x, y), если существует окрестность точки М0 такая, что для всех точек M(x, y) из этой окрестности, отличных от М0, выполняется условие f(x0, y0) > f(x, y) (f(x0, y0) < f(x, y)). Определение 1.11. Внутренние точки из области определения функции, в которых все частные производные первого порядка данной функции либо равны нулю, либо равны бесконечности, либо не существуют, называются критическими точками. При этом те из них, в которых все частные производные первого порядка равны нулю, называются стационарными. Теорема (необходимое условие экстремума). Пусть функция z = f(x, y) достигает экстремума в точке M0(x0, y0), тогда данная точка будет критической для функции z. Замечание. Каждая точка экстремума функции будет её критической точкой, но не каждая критическая точка будет точкой экстремума. Например, поскольку для функции Теорема (достаточное условие экстремума). Пусть в некоторой окрестности критической точки M0(x0, y0) функция z = f(x, y) имеет непрерывные частные производные второго порядка. Обозначим
Тогда если Пример 1.11. Найти экстремумы функции Решение.
Пример 1.12. Найти экстремумы функции Решение. Для М1:
Для М2:
максимума, Для М3:
Для М4:
Пример 1.13. Предприятие производит два вида продукции в количестве x и y. Цена за единицу продукции составляет 8000 гривен и 10000 гривен соответственно, а функция затрат имеет вид Решение. Обозначим функцию прибыли
Ответ. Для максимизации прибыли необходимо производить 2 единицы продукции первого вида и 4 единицы продукции второго вида. Прибыль при таком плане производства составит 28000 гривен. Определение 1.12. Задача нахождения локального экстремума функции Пример 1.14. Найти экстремумы функции z=x2+6x-2y+1 при условии x2+y-4=0. Решение. Воспользуемся методом исключения неизвестной: из уравнения связи x2+y-4=0 находим y=4-x2 и, следовательно, z(x)=x2+6x-2(4-x2)+1. Для данной функции применим алгоритм нахождения экстремумов функции одной переменной. Так как Определение 1.13. Функцией Лагранжа для задачи нахождения экстремума функции
при условии
называется функция Теорема 1.2. Пусть точка Теорема 1.3. Пусть точка
положителен (отрицателен). Тогда точка Пример 1.15. Найти экстремумы функции z=x2+6x-2y+1 при условии x2+y-4=0. Решение. Составим функцию Лагранжа
Таким образом,
Следовательно, точка Пример 1.16. Найти экстремумы функции Решение. Составим функцию Лагранжа
Из второй строки следует, что
Решив каждую из систем, получим координаты критических точек функции
и, следовательно,
и, следовательно,
и, следовательно,
и, следовательно, Тогда, исходя из теоремы 1.2, точки М1 (1, -1) и М2(-1, 1) – точки условного минимума исходной задачи,
Поиск по сайту: |
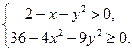 Рассмотрим каждое из этих условий по отдельности:
Рассмотрим каждое из этих условий по отдельности: - это верное неравенство, поэтому первому ограничению удовлетворяют координаты точек, лежащих между ветвями параболы;
- это верное неравенство, поэтому первому ограничению удовлетворяют координаты точек, лежащих между ветвями параболы; или
или 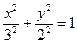 - это уравнение эллипса с центром в точке (0, 0), большей полуосью 3 и меньшей полуосью 2. Поскольку неравенство нестрогое, то эллипс изображен сплошной линией. Для выбора части плоскости, координаты точек которой удовлетворяют неравенству, воспользуемся методом пробной точки: возьмём точку М0(0, 0) (не лежащую на эллипсе) и подставим её координаты в ограничение
- это уравнение эллипса с центром в точке (0, 0), большей полуосью 3 и меньшей полуосью 2. Поскольку неравенство нестрогое, то эллипс изображен сплошной линией. Для выбора части плоскости, координаты точек которой удовлетворяют неравенству, воспользуемся методом пробной точки: возьмём точку М0(0, 0) (не лежащую на эллипсе) и подставим её координаты в ограничение 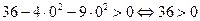 - это верное неравенство, поэтому второму ограничению удовлетворяют координаты точек, лежащих внутри эллипса;
- это верное неравенство, поэтому второму ограничению удовлетворяют координаты точек, лежащих внутри эллипса; называется производственной функцией Кобба-Дугласа, в которой объём производства Q ( V)зависит от двух основных факторов: К—
называется производственной функцией Кобба-Дугласа, в которой объём производства Q ( V)зависит от двух основных факторов: К— ,
,  и А функция Кобба-Дугласа описывает структуру производства некоторой отрасли промышленности. Для построения аналитической зависимости данные обычно поступают в виде статистических таблиц
и А функция Кобба-Дугласа описывает структуру производства некоторой отрасли промышленности. Для построения аналитической зависимости данные обычно поступают в виде статистических таблиц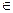 D(z). Это множество, как правило, образует некоторую поверхность в пространстве.
D(z). Это множество, как правило, образует некоторую поверхность в пространстве. , выделив в левой части полный квадрат:
, выделив в левой части полный квадрат:  . Таким образом, картой линий уровня является множество концентрических окружностей с центром в точке (0, 1) и радиусом
. Таким образом, картой линий уровня является множество концентрических окружностей с центром в точке (0, 1) и радиусом  .
. 
 или, возведя обе части в куб,
или, возведя обе части в куб,  . Из данного соотношения следует, что при фиксированном объёме производства величины К и L находятся в обратной зависимости: увеличение капитала, вложенного в производство (например, покупка более совершенных станков), позволяет сократить расходы на рабочую силу.
. Из данного соотношения следует, что при фиксированном объёме производства величины К и L находятся в обратной зависимости: увеличение капитала, вложенного в производство (например, покупка более совершенных станков), позволяет сократить расходы на рабочую силу. по переменной
по переменной 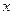 в точке
в точке  называется выражение вида
называется выражение вида  .
.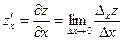 и
и 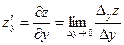 .
. ,
, 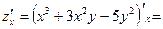
 =
= ,
,  ;
; ,
, 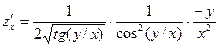 ,
,  ;
; ,
,  ,
, 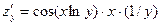 .
.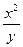 , где x–суммарное число жителей (в тысячах) в городах, y-расстояние между городами. Найти частные производные и пояснить их смысл.
, где x–суммарное число жителей (в тысячах) в городах, y-расстояние между городами. Найти частные производные и пояснить их смысл. - при неизменном расстоянии увеличение потока пассажиров пропорционально удвоенному суммарному числу жителей в городах.
- при неизменном расстоянии увеличение потока пассажиров пропорционально удвоенному суммарному числу жителей в городах.  - при неизменном суммарном числе жителей уменьшение потока пассажиров обратно пропорционально квадрату расстояния между городами. Например, при суммарной численности жителей 1100000 человек и расстоянии 300 километров пассажиропоток составит 4033 человека за месяц. Если, допустим, суммарное число жителей возрастёт на 1 000 человек, то
- при неизменном суммарном числе жителей уменьшение потока пассажиров обратно пропорционально квадрату расстояния между городами. Например, при суммарной численности жителей 1100000 человек и расстоянии 300 километров пассажиропоток составит 4033 человека за месяц. Если, допустим, суммарное число жителей возрастёт на 1 000 человек, то  - пассажиропоток возрастёт приблизительно на 7 человек. Этот же результат можно было получить как
- пассажиропоток возрастёт приблизительно на 7 человек. Этот же результат можно было получить как  (человек).
(человек). , называется величина
, называется величина ,
,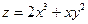 в точке М0(1; 2) по направлению вектора
в точке М0(1; 2) по направлению вектора 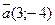 .
.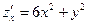 ,
,  ,
, 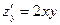 ,
,  ,
, , то
, то 
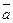 возрастает со скоростью 2,8.
возрастает со скоростью 2,8.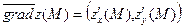 .
. и
и  , то
, то  ,
, 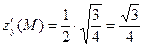 и
и  .
. 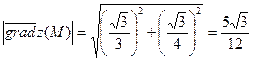 .
. со скоростью
со скоростью 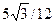 .
. и из системы уравнений
и из системы уравнений
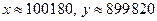 .
. ,
,  ,
,  ,
,  называются частными производными второго порядка. Аналогично определяются и частные производные более высоких порядков.
называются частными производными второго порядка. Аналогично определяются и частные производные более высоких порядков. ,
,  ,
,  ,
,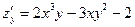 ,
,  ,
,  .
.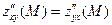 .
.
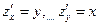 , то точка M0(0, 0)—критическая точка, причём z(M0)=0. Однако для точек М из первой и третьей четвертей, лежащих в окрестности M0, z(M0)<z(M), а для точек М из второй и четвёртой четвертей, лежащих в окрестности M0, z(M0)> z(M). Таким образом, M0 не является ни точкой максимума, ни точкой минимума.
, то точка M0(0, 0)—критическая точка, причём z(M0)=0. Однако для точек М из первой и третьей четвертей, лежащих в окрестности M0, z(M0)<z(M), а для точек М из второй и четвёртой четвертей, лежащих в окрестности M0, z(M0)> z(M). Таким образом, M0 не является ни точкой максимума, ни точкой минимума.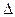 (М0)=
(М0)=  .
. , и точка минимума, если
, и точка минимума, если  ). Если
). Если 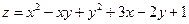 .
. . Найдём критические (стационарные) точки, применяя необходимое условие экстремума. Частные производные имеют вид
. Найдём критические (стационарные) точки, применяя необходимое условие экстремума. Частные производные имеют вид 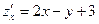 и
и 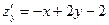 . Из системы уравнений
. Из системы уравнений  найдём координаты критической точки М0(-4/3; 1/3). Проверим, будет ли данная точка точкой экстремума, с помощью достаточного условия экстремума. Частные производные второго порядка имеют вид
найдём координаты критической точки М0(-4/3; 1/3). Проверим, будет ли данная точка точкой экстремума, с помощью достаточного условия экстремума. Частные производные второго порядка имеют вид 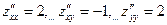 и, вне зависимости от координат М0,
и, вне зависимости от координат М0,  . Поэтому М0 будет являться точкой экстремума функции z, причём точкой минимума, поскольку
. Поэтому М0 будет являться точкой экстремума функции z, причём точкой минимума, поскольку 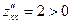 . Найдём экстремум:
. Найдём экстремум: 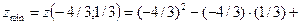
 .
. .
. и
и  . Из системы уравнений
. Из системы уравнений  находим координаты критических точек: М1(0; 0), М2(-5/3; 0), М3(-1; 2) и М4(-1; -2). Проверим, будут ли данные критические точки токами экстремума, с помощью достаточного условия экстремума. Частные производные второго порядка имеют вид
находим координаты критических точек: М1(0; 0), М2(-5/3; 0), М3(-1; 2) и М4(-1; -2). Проверим, будут ли данные критические точки токами экстремума, с помощью достаточного условия экстремума. Частные производные второго порядка имеют вид  ,
, 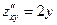 и
и  . Поскольку, в отличии от предыдущего примера, значения производных зависят от координат критических точек, необходимо каждую критическую точку исследовать отдельно.
. Поскольку, в отличии от предыдущего примера, значения производных зависят от координат критических точек, необходимо каждую критическую точку исследовать отдельно.
 - точка минимума,
- точка минимума, 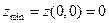 ;
;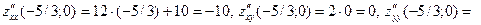
 - точка
- точка ;
;
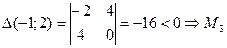 - не является точкой экстремума;
- не является точкой экстремума;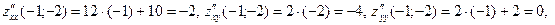
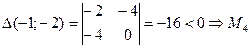 - не является точкой экстремума.
- не является точкой экстремума. . Составить план производства, при котором прибыль предприятия будет максимальной.
. Составить план производства, при котором прибыль предприятия будет максимальной.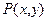 , тогда
, тогда  . Переменные могут принимать только неотрицательные значения. Поскольку
. Переменные могут принимать только неотрицательные значения. Поскольку  и
и  , то из необходимого условия экстремума
, то из необходимого условия экстремума  находим координаты критической точки М0(2; 4). Проверим, является ли данная точка точкой экстремума:
находим координаты критической точки М0(2; 4). Проверим, является ли данная точка точкой экстремума: 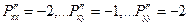 и
и 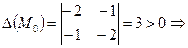 точка М0(2; 4) будет точкой экстремума (максимума с учётом знака
точка М0(2; 4) будет точкой экстремума (максимума с учётом знака  ).
). 
 (тысяч гривен).
(тысяч гривен).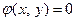 (уравнению связи), называется задачей нахождения условного экстремума.
(уравнению связи), называется задачей нахождения условного экстремума.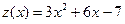 , то
, то  и из уравнения
и из уравнения 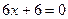 находим, что
находим, что 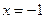 - критическая точка функции
- критическая точка функции  . При переходе через данную точку знак
. При переходе через данную точку знак  меняется с минуса на плюс, поэтому
меняется с минуса на плюс, поэтому 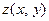 ,
,  .
.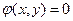 (2)
(2) , в которой
, в которой  - вспомогательная переменная (множитель Лагранжа).
- вспомогательная переменная (множитель Лагранжа). является точкой локального экстремума функции Лагранжа, соответствующей задаче (1)-(2). Тогда точка
является точкой локального экстремума функции Лагранжа, соответствующей задаче (1)-(2). Тогда точка  будет точкой условного экстремума задачи (1)-(2).
будет точкой условного экстремума задачи (1)-(2). и определитель
и определитель
 . Первый этап: найдём критические точки функции L. Поскольку
. Первый этап: найдём критические точки функции L. Поскольку 
 , то из необходимого условия локального экстремума получим систему уравнений
, то из необходимого условия локального экстремума получим систему уравнений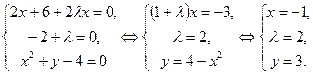
 - критическая точка функции
- критическая точка функции  . Второй этап: проверим, является ли данная точка точкой экстремума функции
. Второй этап: проверим, является ли данная точка точкой экстремума функции  , то
, то .
. .
. .
.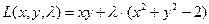 . Первый этап: найдём критические точки функции L. Поскольку
. Первый этап: найдём критические точки функции L. Поскольку 
 , то из необходимого условия локального экстремума получим систему уравнений
, то из необходимого условия локального экстремума получим систему уравнений
 и
и  (случай
(случай 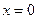 не подходит, поскольку тогда первая строка системы противоречит третьей). Таким образом
не подходит, поскольку тогда первая строка системы противоречит третьей). Таким образом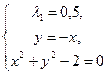 или
или 
 ,
, 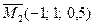 - решения первой системы;
- решения первой системы;  ,
, 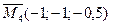 - решения второй системы. Второй этап: проверим, являются ли данные точки точками экстремума функции
- решения второй системы. Второй этап: проверим, являются ли данные точки точками экстремума функции  . Поскольку у функции
. Поскольку у функции 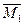 :
:  , тогда
, тогда
 :
:  , тогда
, тогда
 :
: 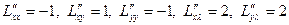 , тогда
, тогда
 :
:  , тогда
, тогда
 , а точки М3(1, 1) и М4(-1, -1) – точки условного максимума исходной задачи,
, а точки М3(1, 1) и М4(-1, -1) – точки условного максимума исходной задачи, 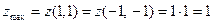 .
.