 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
III. Дифференциальные уравненияСтр 1 из 2Следующая ⇒
Определение 3.1. Обыкновенным дифференциальным уравнением называется уравнение, связывающее искомую функцию одной переменной, саму переменную и производные (или дифференциалы) различных порядков данной функции. Порядком дифференциального уравнения называется наивысший порядок производной, входящей в это уравнение. Пример 3.1.Укажите порядок следующих уравнений:
Определение 3.2. Решением дифференциального уравнения называется функция y(x), которая при подстановке в уравнение обращает его в тождество. График функции y(x) называется интегральной кривой. Пример 3.2. Показать, что функция Решение. Поскольку Определение 3.3. Общим решением дифференциального уравнения n–го порядка называется функция Пример 3.3. Для уравнения а) не является решением; б) является решением; в) является общим интегралом; г) является общим решением. Решение. Ответ в) не подходит, поскольку функция Определение 3.4. Частным решением дифференциального уравнения называется решение, получаемое из общего при конкретных значениях постоянных С1, С2, …, Сn. Пример 3.4. Показать, что функция Решение. Найдём Определение 3.5. Задачей Коши называется совместное задание дифференциального уравнения и соответствующего количества начальных условий, необходимых для определения постоянных С1, С2, …, Сn. Пример 3.5. Решить задачу Коши Решение. Ранее было показано, что общим решением дифференциального уравнения является функция
Из неё следует, что С1= 1 и С2= -1. Поэтому решение задачи Коши имеет вид Пример 3.6. В комнате, где температура 200 С, некоторое тело охладилось за 20 минут от 1000 С до 600 С. Найти закон изменения температуры тела и определить, через сколько минут охладится до 300 С. Какой будет температура тела через 40 минут после начала охлаждения? Решение. Согласно закону излучения тепла скорость охлаждения пропорциональна разности температур тела и окружающей среды, то есть
Пример 3.7. Пусть количество потенциальных покупателей товара А составляет 100 000 человек. Обозначим y(t)--число потенциальных покупателей товара А в момент времени t. Для стимуляции сбыта была начата рекламная компания. Известно, что после начала рекламной компании скорость изменения числа покупателей, знающих о товаре А, пропорциональна как числу знающих про товар, так и не знающих. Составить закон изменения, если в момент начала рекламной компании про товар А знала половина потенциальных покупателей. Решение. Математическая модель задачи имеет вид
Из условия
Дифференциальные уравнения I–го порядка. Определение 3.6. Дифференциальным уравнением I–го порядка называется уравнение вида
Определение 3.7. Дифференциальное уравнение I–го порядка называется уравнением с разделяющимися переменными, если оно представимо в виде
Пример 3.8. Найти общее решение (общий интеграл) Д.У. Решение. Из данного уравнения следует, что либо
Пример 3.9. Решить задачу Коши: Решение.
Пример 3.10. Найти общее решение (общий интеграл) дифференциального уравнения
Решение. Пример 3.11. Предельные затраты производства равны удвоенным средним. Найти функцию полных затрат, которая удовлетворяет условию y(10)=1. Решение. Пусть x – объём производства (независимая переменная), y – соответствующие полные затраты производства (зависимая переменная). Поскольку предельные затраты имеют вид
Пример 3.12. Заданы функции спроса и предложения некоторого товара
где t-time–время, p-price-цена, s-supply-предложение, d-demand-спрос. Необходимо: а) найти равновесную цену как функцию от времени, если p(0)=17; б) определить, будет ли данная цена стабильной. Решение. а) Найдём равновесную цену из дифференциального уравнения
б) Поскольку Определение 3.8. Дифференциальное уравнение I–го порядка называется линейным, если его можно привести к виду: Пример 3.13. Найти общее решение уравнения Решение. Положим Пример 3.14. Решить задачу Коши Решение. Преобразуем исходное уравнение
Пример 3.15. Найти общее решение уравнения Решение. В данном уравнении проще рассматривать y как независимую переменную, а x(y) – как функцию. Тогда Пример 3.16. Ежедневный уровень выпуска продукции растёт со средним темпом 0,33%. Определить закон изменения уровня выпуска продукции со временем и объём выпуска за 30 дней, если уровень выпуска на начало месяца составляет 1000 единиц продукции в сутки. Решение. Пусть x – количество дней, прошедших с начала месяца, y - уровень выпуска продукции в соответствующий день. Тогда, исходя из условия, имеет место соотношение
Дифференциальные уравнения II–го порядка. Определение 3.9. Дифференциальным уравнением II-го порядка называется уравнение вида
Определение 3.10. Дифференциальное уравнение II-го порядка называется уравнением, допускающим понижение порядка, если оно может быть представлено в виде
Решаются такие уравнения с помощью замены искомой функции. Пример 3.17. Найти общее решение дифференциального уравнения Решение. Сделаем замену Пример 3.18. Найти общее решение дифференциального уравнения Решение. Сделаем замену Определение 3.11. Дифференциальное уравнение II-го порядка называется линейным однородным уравнением с постоянными коэффициентами, если оно может быть представлено в виде
где b, c – некоторые числа. Определение 3.12. Уравнение
называется характеристическим уравнением, соответствующим уравнению (1). Оно получается из уравнения (1) путём преобразования Теорема 3.1. а) Если уравнение (2) имеет два различных действительных корня общее решение уравнения (1) имеет вид б) Если уравнение (2) имеет один действительный корень кратности, то общее решение уравнения (1) имеет вид в) Если уравнение (2) не имеет действительных корней, то общее решение уравнения (1) имеет вид
Пример 3.19. Найти общее решение дифференциального уравнения Решение. Характеристическое уравнение имеет вид Пример 3.20. Найти решение задачи Коши Решение. Для дифференциального уравнения Пример 3.21. Найти общее решение дифференциального уравнения Решение. Характеристическое уравнение имеет вид Определение 3.13. Дифференциальное уравнение II-го порядка называется линейным неоднородным уравнением с постоянными коэффициентами, если оно может быть представлено в виде
где b, c – некоторые числа, z(x) – функция переменной x. Теорема 3.2. Общее решение уравнения (3) равно сумме общего решения соответствующего ему уравнения (1) и произвольного частного решения уравнения (3)
Замечание. Если правая часть уравнения (3) имеет вид
Пример 3.22. Найти общее решение дифференциального уравнения Решение.
Воспользовавшись методом неопределённых коэффициентов, получим систему уравнений
следовательно, Пример 3.23. Найти общее решение дифференциального уравнения Решение.
Воспользовавшись методом неопределённых коэффициентов, получим систему уравнений
следовательно, Пример 3.24. Найти общее решение дифференциального уравнения Решение. Найдём
Воспользовавшись методом неопределённых коэффициентов, получим систему уравнений
следовательно,
Поиск по сайту: |
 ,
,  ,
, .
. является решением уравнения
является решением уравнения  .
. и
и 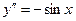 , то при подстановке
, то при подстановке  и
и  в исходное уравнение получаем тождество
в исходное уравнение получаем тождество  .
. , зависящая от аргумента x и n независимых произвольных постоянных, которая при подстановке в уравнение обращает его в тождество. Если в общем решении функция
, зависящая от аргумента x и n независимых произвольных постоянных, которая при подстановке в уравнение обращает его в тождество. Если в общем решении функция  функция
функция 
 и
и  . Подставив представления для
. Подставив представления для  является общим решением уравнения
является общим решением уравнения  и указать несколько частных решений данного уравнения.
и указать несколько частных решений данного уравнения. и
и  . Подставив представления в уравнение, получим тождество. Следовательно, функция является решением исходного уравнения. Кроме того, поскольку она содержит две независимые постоянные и является решением уравнения второго порядка, то она является общим решением уравнения. Частными решениями данного уравнения являются, например, функции
. Подставив представления в уравнение, получим тождество. Следовательно, функция является решением исходного уравнения. Кроме того, поскольку она содержит две независимые постоянные и является решением уравнения второго порядка, то она является общим решением уравнения. Частными решениями данного уравнения являются, например, функции  и
и  .
.
 и
и  , получим систему линейных алгебраических уравнений
, получим систему линейных алгебраических уравнений
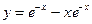 .
. , где y(t)- температура тела в момент времени t, a- температура окружающей среды, k- положительное число (коэффициент пропорциональности). Указанное уравнение является уравнением с разделяющимися переменными
, где y(t)- температура тела в момент времени t, a- температура окружающей среды, k- положительное число (коэффициент пропорциональности). Указанное уравнение является уравнением с разделяющимися переменными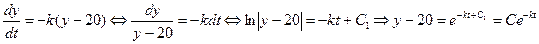 и
и  . Воспользовавшись начальными условиями
. Воспользовавшись начальными условиями 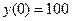 и
и 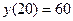 , получим систему алгебраических уравнений
, получим систему алгебраических уравнений . Тогда закон охлаждения тела имеет вид
. Тогда закон охлаждения тела имеет вид  . Для ответа на вопрос, через сколько времени температура тела составит 300, необходимо решить уравнение
. Для ответа на вопрос, через сколько времени температура тела составит 300, необходимо решить уравнение 
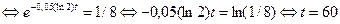 --через 60 минут. Для ответа на вопрос, какой будет температура тела через 40 минут после начала охлаждения, необходимо вычислить
--через 60 минут. Для ответа на вопрос, какой будет температура тела через 40 минут после начала охлаждения, необходимо вычислить 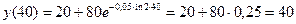 0С.
0С. 
 . Это задача Коши, содержащая уравнение с разделяющимися переменными.
. Это задача Коши, содержащая уравнение с разделяющимися переменными.

 находим
находим  и
и 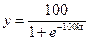 -- графиком этой функции является логистическая кривая. Коэффициент k выбирается с учётом специфики товара (товар первой необходимости, предмет роскоши,…). Исходя из вида логистической кривой можно сделать вывод, что после определённого момента времени продолжать рекламную компанию не следует, поскольку целевая аудитория изменяется незначительно.
-- графиком этой функции является логистическая кривая. Коэффициент k выбирается с учётом специфики товара (товар первой необходимости, предмет роскоши,…). Исходя из вида логистической кривой можно сделать вывод, что после определённого момента времени продолжать рекламную компанию не следует, поскольку целевая аудитория изменяется незначительно. или
или  .
. или
или  .
. .
. , либо
, либо  , либо
, либо 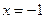 . Последние два случая описывают особые решения, исключим их из рассмотрения.
. Последние два случая описывают особые решения, исключим их из рассмотрения. - общий интеграл. Преобразуем данное соотношение, заменив постоянную
- общий интеграл. Преобразуем данное соотношение, заменив постоянную  на
на  . Тогда из
. Тогда из находим
находим  - общее решение. Заметим, что при С=0 из общего решения можно получить особое.
- общее решение. Заметим, что при С=0 из общего решения можно получить особое.
 (поскольку случай х=0 не соответствует начальному условию). Проинтегрировав обе части, получим общий интеграл:
(поскольку случай х=0 не соответствует начальному условию). Проинтегрировав обе части, получим общий интеграл:  Из начального условия
Из начального условия 
 и, окончательно,
и, окончательно,  -решение задачи Коши.
-решение задачи Коши.
 и y=0-особое решение. Интегрируя левую и правую части дифференциального уравнения с разделёнными переменными (правую с помощью метода замены переменной), получим
и y=0-особое решение. Интегрируя левую и правую части дифференциального уравнения с разделёнными переменными (правую с помощью метода замены переменной), получим  - общее решение. Заметим, что в данном примере, в отличие от примера 3.8, особое решение невозможно получить из общего.
- общее решение. Заметим, что в данном примере, в отличие от примера 3.8, особое решение невозможно получить из общего. , то из условия получаем дифференциальное уравнение первого порядка с разделяющимися переменными:
, то из условия получаем дифференциальное уравнение первого порядка с разделяющимися переменными: 
 и
и  . Поскольку
. Поскольку  , то
, то  . Следовательно, функция полных затрат имеет вид
. Следовательно, функция полных затрат имеет вид 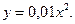
 ,
,  ,
,
 :
: 

 . Так как
. Так как  , то из уравнения
, то из уравнения находим
находим  и, окончательно,
и, окончательно,  .
. , то равновесная цена является нестабильной.
, то равновесная цена является нестабильной. , где f(x) и g(x)—непрерывные функции. Если
, где f(x) и g(x)—непрерывные функции. Если  , то такое уравнение называется однородным, в противном случае—неоднородным. Решаются данные уравнения с помощью замены
, то такое уравнение называется однородным, в противном случае—неоднородным. Решаются данные уравнения с помощью замены  , где
, где  и
и  - специально подобранные функции (метод Бернулли).
- специально подобранные функции (метод Бернулли). .
. . Подставив эти представления в исходное уравнение, получим
. Подставив эти представления в исходное уравнение, получим  или
или  . Первый этап: найдём функцию
. Первый этап: найдём функцию  (при нахождении интеграла от правой части применили метод замены переменной). Второй этап: подставим полученное представление для
(при нахождении интеграла от правой части применили метод замены переменной). Второй этап: подставим полученное представление для  . Поэтому общее решение исходного уравнения имеет вид
. Поэтому общее решение исходного уравнения имеет вид  .
.

 . Первый этап: найдём функцию
. Первый этап: найдём функцию  . Второй этап: подставим полученное представление для
. Второй этап: подставим полученное представление для  (при нахождении интеграла от правой части применили метод интегрирования по частям). Тогда
(при нахождении интеграла от правой части применили метод интегрирования по частям). Тогда  . Из начального условия
. Из начального условия  находим
находим  и решение задачи Коши имеет вид
и решение задачи Коши имеет вид  .
. .
. . Пусть
. Пусть  , тогда уравнение примет вид
, тогда уравнение примет вид  . Первый этап: найдём функцию
. Первый этап: найдём функцию  из условия
из условия  . Второй этап: подставим полученное представление для
. Второй этап: подставим полученное представление для 
 и общее решение исходного уравнения имеет вид
и общее решение исходного уравнения имеет вид 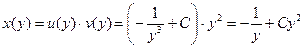 .
. , и, учитывая
, и, учитывая  , получим, что закон изменения выпуска продукции имеет вид
, получим, что закон изменения выпуска продукции имеет вид  . Суммарный выпуск продукции за 30 дней составит приблизительно
. Суммарный выпуск продукции за 30 дней составит приблизительно  единиц продукции.
единиц продукции. .
.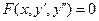 или
или  .
. .
. , тогда
, тогда  и уравнение примет вид
и уравнение примет вид  . Это уравнение с разделяющимися переменными, из которого следует, что либо
. Это уравнение с разделяющимися переменными, из которого следует, что либо  , либо
, либо 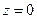 (и тогда y=Const), либо x=0.
(и тогда y=Const), либо x=0.  . Сделав обратную замену, получим
. Сделав обратную замену, получим  - общее решение исходного уравнения (при С1
- общее решение исходного уравнения (при С1  0).
0). .
. , тогда
, тогда  и уравнение примет вид
и уравнение примет вид  . Это уравнение с разделяющимися переменными, из которого следует, что либо
. Это уравнение с разделяющимися переменными, из которого следует, что либо  , либо
, либо  или
или  - общее решение исходного уравнения.
- общее решение исходного уравнения. , (1)
, (1) (2)
(2) .
.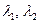 , то
, то ;
; двойной
двойной ;
; , где
, где .
. .
. , его корни
, его корни  . Это случай а), поэтому
. Это случай а), поэтому  .
.
 характеристическое уравнение имеет вид
характеристическое уравнение имеет вид  . Поскольку
. Поскольку  , это случай б) и общим решением будет функция
, это случай б) и общим решением будет функция  . Для того, чтобы воспользоваться вторым из начальных условий, необходимо найти
. Для того, чтобы воспользоваться вторым из начальных условий, необходимо найти  . Тогда из системы линейных уравнений
. Тогда из системы линейных уравнений  находим
находим  . Следовательно, решение задачи Коши имеет вид
. Следовательно, решение задачи Коши имеет вид  .
.  .
. .
.  это случай в). Вычислим
это случай в). Вычислим  , тогда
, тогда  .
. , (3)
, (3) .
. , где
, где 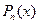 - многочлен степени n, то частное решение уравнения (3) будем искать в виде
- многочлен степени n, то частное решение уравнения (3) будем искать в виде  , где Qn(x) – многочлен степени n с произвольными коэффициентами, а s определяется следующим образом
, где Qn(x) – многочлен степени n с произвольными коэффициентами, а s определяется следующим образом
 .
. (смотри пример 3.19); n=1, r= -1
(смотри пример 3.19); n=1, r= -1  s=0 и
s=0 и  . Найдём
. Найдём  и
и  . Подставив эти представления в исходное уравнение, получим соотношение
. Подставив эти представления в исходное уравнение, получим соотношение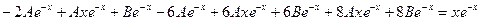 .
.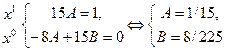
 и
и  .
. .
. . Найдём
. Найдём  и
и  . Подставив эти представления в исходное уравнение, получим соотношение
. Подставив эти представления в исходное уравнение, получим соотношение .
.
 и
и  .
. .
. .
. и
и  . Подставив эти представления в исходное уравнение, получим соотношение
. Подставив эти представления в исходное уравнение, получим соотношение .
.
 и
и  .
.