 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Лемма Больцано-Вейерштрасса ⇐ ПредыдущаяСтр 2 из 2
Из всякой ограниченной числовой последовательности можно выделить сходящуюся подпоследовательность. 14. Всякая ограниченная числовая последовательность имеет хотя бы одну предельную точку.
Эта лемма и ее следствия имеют больше теоретический смысл, чем практический. Они используются в дальнейшем для доказательства других важных теорем.
27 Предельная точка числовой последовательности. Предельные точки сходящейся числовой последовательности. Существование предельной точки у ограниченной числовой последовательности Понятия 26. Предельной точкой числовой последовательности Утверждения 12. У сходящейся числовой последовательности существует одна и только одна предельная точка. 14. Всякая ограниченная числовая последовательность имеет хотя бы одну предельную точку. Умения 1. Может ли у монотонной ограниченной последовательности быть две предельные точки? Решение. Монотонная ограниченная последовательность всегда является сходящейся, а у сходящейся последовательности есть ровно одна предельная точка, поэтому ответ «нет».
2.Может ли у бесконечно большой последовательности быть предельная точка? Решение. Если есть предельная точка, значит, есть некоторая подпоследовательность, сходящаяся к этой точке. А раз так, значит, есть ограниченная подпоследовательность, то есть исходная последовательность не может быть бесконечно большой. 28 Нахождение предельных точек числовой последовательности
Для того, чтобы найти предельные точки числовой последовательности, необходимо выделить сходящиеся подпоследовательности.
Умения 1. Найти все предельные точки последовательности Решение. При При При Мы рассмотрели все возможные варианты для n и получили, что у данной последовательности есть 3 предельные точки. Это 2,
2. Найти все предельные точки последовательности Решение. При При При При Таким образом, у данной последовательности 4 предельные точки. Это 3. Найти предельные точки последовательности Решение. Рассмотрим при
Рассмотрим при
Данная последовательность имеет две предельных точки 1 и -1.
29 Верхний и нижний пределы числовой последовательности
Понятия 27. Нижний (верхний) предел числовой последовательности - это наименьшая (наибольшая) из предельных точек.
Чтобы найти верхний и нижний пределы числовой последовательности, для начала нам нужно найти ее предельные точки, а затем выбрать наибольшую и наименьшую из них.
Умения 1. Найти нижний предел последовательности Решение. При четных n получаем При нечетных n получаем Других предельных точек нет, то есть нижний предел равен
2. Найти верхний предел последовательности Решение. При четных n При При То есть верхний предел последовательности это 3. Дана числовая последовательность Решение. Рассмотрим при
Рассмотрим при
Наибольший частичный предел равен 1
4.Дана последовательность Решение. Рассмотрим при
Рассмотрим при
Наименьший частичный предел равен 0, поэтому нижний предел данной последовательности:
30 Фундаментальные числовые последовательности (последовательности Коши) и их свойства. Вспомогательный критерий сходимости. Критерий сходимости Коши Понятия 28. Числовая последовательность называется фундаментальной (последовательностью Коши), если Утверждения 15.Свойства: 1о. Всякая фундаментальная последовательность является ограниченной. 2о. Если
16. Вспомогательный критерий сходимости:
17. Критерий сходимости Коши:
Умения 1. Рассмотрим последовательность Решение. Для любого n выполняется
2. Пусть Решение. Пусть m>n. Оценим разность xm-xn
Таким образом, подбирая по заданному ε>0 натуральное число K так, что 3. Дана числовая последовательность Доказать, что она является нефундаментальной.
Решение. Очевидно, что И если взять 4. Дана числовая последовательность Решение. Рассмотрим предел данной последовательности при
и рассмотрим предел при
Ответ: так как пределы равны, то последовательность фундаментальна.
Поиск по сайту: |
 называется такое число x0, что в любой его ε - окрестности содержится бесконечно много членов последовательности
называется такое число x0, что в любой его ε - окрестности содержится бесконечно много членов последовательности  .
. ,
, 
 . Эта подпоследовательность сходится к 2.
. Эта подпоследовательность сходится к 2. или
или  ,
,  . Эта подпоследовательность сходится к
. Эта подпоследовательность сходится к 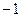 .
.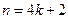 ,
,  . Эта подпоследовательность сходится к
. Эта подпоследовательность сходится к  .
. .
.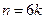 ,
,  .
. ,
, 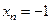 .
. или
или  ,
,  .
.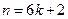 или
или 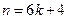 ,
,  .
. .
.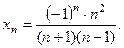


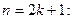

 .
. . Предел этой подпоследовательности равен 1.
. Предел этой подпоследовательности равен 1.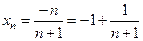 . Предел этой подпоследовательности равен
. Предел этой подпоследовательности равен 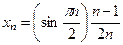 .
. .
. .
. .
.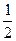 .
. Найти верхний предел.
Найти верхний предел.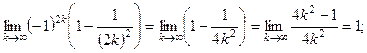



 Найти ее нижний предел.
Найти ее нижний предел.


 .
. фундаментальная числовая последовательность, то
фундаментальная числовая последовательность, то  , такое что вне
, такое что вне 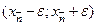 содержится не более чем конечное число членов
содержится не более чем конечное число членов  . Имеет ли она предел?
. Имеет ли она предел? . Таким образом, эта последовательность не является фундаментальной, а значит, в силу критерия Коши она не является сходящейся.
. Таким образом, эта последовательность не является фундаментальной, а значит, в силу критерия Коши она не является сходящейся. … некоторая последовательность конечных десятичных дробей, причем каждая следующая дробь получается из предыдущей дописыванием одной любой цифры. Показать, что такая последовательность всегда сходится.
… некоторая последовательность конечных десятичных дробей, причем каждая следующая дробь получается из предыдущей дописыванием одной любой цифры. Показать, что такая последовательность всегда сходится.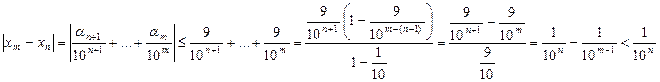 .
. , для любых
, для любых  , получим оценку
, получим оценку  , которая доказывает фундаментальность, а значит и сходимость последовательности.
, которая доказывает фундаментальность, а значит и сходимость последовательности. .
.
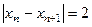 .
.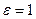 , то получим отрицание утверждения, что последовательность фундаментальна.
, то получим отрицание утверждения, что последовательность фундаментальна. . Доказать, что она является фундаментальной.
. Доказать, что она является фундаментальной.
