 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Связь сходящейся и бесконечно малой последовательностиСтр 1 из 2Следующая ⇒
Таблица расстановки понятий по учебным элементам структуры теста МА–Т–02 «Числовая последовательность и ее предел»
Таблица расстановки утверждений по учебным элементам структуры теста МА–Т–02 «Числовая последовательность и ее предел»
Таблица расстановки умений по учебным элементам структуры теста МА–Т–02 «Числовая последовательность и ее предел»
I. Понятие числовой последовательности 1 Понятие числовой последовательности. Общий член числовой последовательности. График числовой последовательности Понятия 1. Числовая последовательность – функция натурального аргумента. Область определения этой функции – все действительные числа. 2. Общий член числовой последовательности. 4. График числовой последовательности это множество точек
Умения 1. Найти общий член последовательности f(x)=[x] и описать вид графика. Решение: Так как последовательность – это функция натурального аргумента, значит, целая часть от х будет равна самому х. То есть общий член этой числовой последовательности
2. Может ли график числовой последовательности совпадать с графиком непрерывной на всей числовой оси функции? Ответ: Нет. Так как график последовательности это всегда отдельно стоящие точки с натуральной абсциссой, а график непрерывной на всей числовой оси функции проходит и через точки с ненатуральной абсциссой.
3. Может ли график последовательности проходить через точку Ответ. Да, может. Например, график последовательности
4.Является ли данная последовательность Решение: Если приравнять 5. Дана числовая последовательность {0,1,2,3…} Среди этих вариантов выбрать общий член для данной последовательности: Решение: При При При 2 Рекуррентный способ задания числовой последовательности, нахождение формулы общего члена по рекуррентному соотношению Понятия 3. Рекуррентный способ задания числовой последовательности.Если каждый член числовой последовательности выражается через один или несколько предыдущих, то говорят, что эта последовательность задана рекуррентно.
К сожалению, общего алгоритма нахождения формулы общего члена по рекуррентному соотношению нет. Обычно выписывают несколько первых членов и пытаются установить закономерность. Либо выдвигают какую-либо гипотезу, а потом доказывают получившуюся формулу по методу математической индукции.
Умения 1. Найти общий член последовательности Решение: Распишем формулу для xn
То есть, мы получили формулу общего члена
2. Докажите, что общим членом последовательности
Решение: Для Пусть для Рассмотрим n=k+1
Таким образом, по методы математической индукции, получаем, что формулой общего члена действительно является
3. Дана числовая последовательность, заданная рекуррентно Найти формулу общего члена для данной последовательности. Решение: Выразим через рекуррентную формулу
Выразим
… Формула общего члена данной последовательности будет иметь вид:
3 Ограниченные и неограниченные числовые последовательности
Понятия 9. Числовая последовательность 10. Числовая последовательность 11. 12.Последовательность .
Определять ограниченность (неограниченность) последовательности можно построением графика или просто рассуждая. В разных случаях по-разному. Разберем примеры.
Умение 1. Является ли ограниченной последовательность Решение: Заметим, что все члены последовательности лежат на параболе, ветки которой направлены вниз, то есть члены этой последовательности не превышают значения ординаты вершины этой параболы. Следовательно, эта последовательность ограниченна сверху. Снизу она не ограниченна, так как ветки этой параболы уходят в минус бесконечность, т.е. какое бы мы число не взяли, всегда найдутся члены последовательности, которые меньше этого числа.
2. Какой является последовательность Решение: Прикинем, как пойдет график данной последовательности. 3.Исследовать на ограниченность числовую последовательность Доказать что данная числовая последовательность ограничена. Решение:
4. Исследовать на неограниченность числовую последовательность Доказать что данная числовая последовательность неограниченна. Решение:
5. Дана последовательность Доказать, что: ограничена снизу и неограничена сверху при неограничена снизу и ограничена сверху при Решение: Рассмотрим
Очевидно, что эта последовательность ограничена снизу и неограничена сверху, так как добавляя к 1 число Рассмотрим
Данная последовательность неограниченна снизу и ограничена сверху по аналогичной причине.
4 Периодические числовые последовательности Понятия 14. Периодической числовой последовательностью называется последовательность, для которой для любого n выполняется равенство
Умения 1. Является ли периодической последовательность Решение. Чтобы легче было определить ее периодичность или непериодичность вычислим несколько первых членов, начиная с первого. Получаем -2 -2 2 2 2 -2 -2 -2 2 2 2 -2 -2 -2…. По первым членам последовательности видно, что она периодична и период равен 6. Но мы можем ошибиться, поэтому необходимо проверить нашу гипотезу. Рассмотрим yk+6.
2. Найти период последовательности Решение. Выпишем несколько первых членов последовательности: 1, -1, 0, -1, 1, 0, 1, -1, 0, -1, 1, 0… Похоже на то, что периодом является число 6. Проверим это Получаем, что 3. Исследовать числовую последовательность на периодичность. Дана последовательность Исследовать ее на периодичность. Решение. Эта функция является периодической, так как
1 так же является периодом для
II. Бесконечно малые и бесконечно большие числовые последовательности 5 Понятие бесконечно малой числовой последовательности
Понятия 23. Последовательность
То есть, эта последовательность стремится к нулю.
Умения 1. Является ли последовательность Решение. Зафиксируем произвольное ε>0. Модуль xn должен быть меньше ε, но наша последовательность состоит лишь из положительных членов, поэтому можно брать без модуля. Итак, Мы смогли найти
2. Является ли бесконечно малой последовательность Решение. Зафиксируем произвольное 3. Дана числовая последовательность Доказать, что она является бесконечно малой. Решение.
6 Понятие бесконечно большой числовой последовательности Понятия 22. Числовая последовательность Умения 1. Доказать, что последовательность Решение. Зафиксируем произвольное
Итак,
Значит, при 2. Дана числовая последовательность Доказать, что она является бесконечно большой. Решение.
Начиная с номера
7 Свойства бесконечно малых и бесконечно больших последовательностей
Утверждения 4. Свойства бесконечно малых и бесконечно больших числовых последовательностей: 1о. Сумма двух бесконечно малых последовательностей есть последовательность бесконечно малая. 2о. Сумма конечного числа бесконечно малых последовательностей есть последовательность бесконечно малая. 3о. Сумма двух бесконечно больших последовательностей есть последовательность бесконечно большая. 4о. Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность. 5о. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть последовательность бесконечно малая. 6о. Произведение ограниченной последовательности на бесконечно малую последовательность есть последовательность бесконечно малая. 7о. Произведение сходящейся последовательности на бесконечно малую последовательность есть последовательность бесконечно малая. 8о. Произведение двух бесконечно малых последовательностей есть последовательность бесконечно малая. 9о. Модуль бесконечно малой последовательности есть последовательность бесконечно малая. Связь сходящейся и бесконечно малой последовательности. Последовательность сходится и Умения 1. Какой будет последовательность Решение.
2. Будет ли бесконечно малой последовательностью последовательность Решение. Последовательности
3. Если последовательность Решение. По свойству (8), последовательность
8 Связь между бесконечно большими и бесконечно малыми числовыми последовательностями. Связь между бесконечно большой и неограниченной числовой последовательностью
Утверждения: 5. Если последовательность
Всякая бесконечно большая последовательность является неограниченной, обратное, вообще говоря, неверно.
Умения 1. Какой будет являться последовательность Решение.
то в итоге мы получаем бесконечно большую последовательность.
III. Сходящиеся числовые последовательности 9 Предел числовой последовательности. Геометрический смысл предела числовой последовательности Понятия 19. Предел числовой последовательности. Числовая последовательность имеет конечный предел а, если Утверждения 1. Геометрический смысл предела. Если предел последовательности равен ато в любой окрестности этой точки будет содержаться бесконечное количество членов последовательности, а вне ее лишь конечное. Умения 1. Доказать, чтопоследовательность Решение. Нетрудно заметить, что при больших n числитель и знаменатель будут практически одинаковыми, то есть можно предположить, что пределом этой последовательности будет 1. Проверим. Для этого достаточно показать, что последовательность
10 Сходящиеся и расходящиеся числовые последовательности. Их свойства
Понятия 20. Если последовательность имеет конечный предел, то она сходящаяся. 21. Если последовательность не имеет конечного предела, то она расходящаяся.
Свойства сходящихся и расходящихся числовых последовательностей: 1о.Последовательность может иметь не более одного предела. 2о.Сходящаяся последовательность ограничена. 3о. Сумма двух сходящихся последовательностей есть последовательность сходящаяся и ее предел равен сумме пределов слагаемых. 4о. Разность двух сходящихся последовательностей есть последовательность сходящаяся и ее предел равен разности пределов этих последовательностей. 5о. Произведение двух сходящихся последовательностей есть последовательность сходящаяся и ее предел равен произведению пределов сомножителей. 6о. Частное двух сходящихся последовательностей (при условии, что предел делителя не равен 0) есть последовательность сходящаяся и ее предел равен частному пределов этих последовательностей.
Умения 1. Пусть даны 3 сходящиеся последовательности Решение. Из свойств о разности и произведении двух сходящихся последовательностей можно сделать вывод, что данная последовательность сходится. Из тех же свойств получаем, что ее предел равен
2. Найти предел последовательности Решение.
3. Верно ли, что последовательность Решение. Из первого свойства следует, что последовательность не может иметь двух пределов, то есть это утверждение не верно. Данная последовательность вообще не имеет предела, так как если рассмотреть ε – окрестность 1 и -1 при ε=0.5, то получим, что и в том и в другом случае и в окрестности и за ее пределами бесконечное число членов последовательности, что противоречит геометрическому смыслу предела. 4. Дана числовая последовательность Доказать, что она сходится. Решение. Так как последовательность содержит Получаем: При
При
Из того, что значения пределов равны, следует, что исходная числовая последовательность сходится. 5. Дана числовая последовательность Доказать, что она расходится. Решение. Так как последовательность содержит Получаем: При
При
Так как значения пределов не равны, значит, что числовая последовательность расходится. 11 Нахождение номера элемента, начиная с которого все члены последовательности попадают в заданную ε-окрестность числа, символов - Понятия 15. ε- окрестность числа а. 16. ε- окрестность 17. ε- окрестность 18. ε-окрестность Умения 1.Найти номер, начиная с которого все члены последовательности Решение. В общем случае, нам надо найти номер Сформулируем это условие для нашей конкретной задачи: найти
Так как n натуральное, то
2. Найти номер, начиная с которого все члены последовательности Решение. Нужно найти номер В данном конкретном случае мы ищем Итак,
Так как n натуральное, то ( Для - 3. Найти номер, начиная с которого все члены последовательности Решение. Нужно найти номер В нашем случае надо найти номер
Значит, 4. Дана последовательность Найти номер, начиная с которого данная последовательность находится в Решение.
Начиная с 5. Дана последовательность Найти номер, начиная с которого данная последовательность находится в Решение.
Ответ: начиная с
12 Необходимое условие сходимости числовой последовательности. Единственность предела числовой последовательности Утверждения 2. Числовая последовательность может иметь не более одного предела. 3. Теорема об ограниченности сходящейся числовой последовательности. Всякая сходящаяся числовая последовательность является ограниченной, но не всякая ограниченная числовая последовательность является сходящейся. Умения 1. Верно ли, что любая ограниченная последовательность является сходящейся? Решение. Нет, не верно. Приведем пример. Последовательность
2. Имеет ли предел числовая последовательность, у которой две предельные точки? Решение. Если функция имеет предел а, то в любой его ε-окрестности содержится бесконечно много членов последовательности, а за ее пределами лишь конечное. Если у последовательности 2 предельные точки, то если за ε взять треть расстояния между этими точками, то вне ε-окрестностей этих точек будет бесконечно много членов последовательности, то есть эти точки не могут быть пределами. Если предположить, что пределом является какое-то другое число, то если за ε взять треть минимального из расстояний от этого числа до двух предельных точек, то получим, что вне ε-окрестности этого числа бесконечно много членов последовательности. Таким образом, такая последовательность предела не имеет.
13 Предел суммы, разности, произведения и частного двух сходящихся числовых последовательностей
Понятия 5. Суммой двух числовых последовательностей 6. Разностьюдвух числовых последовательностей 7. Произведением двух числовых последовательностей 8. Частнымдвух числовых последовательностей Утверждения 7.1. Если
7.2.Если
7.3.Если 7.4. Если Умения 1. Найти предел последовательности Решение.
2. Найти предел последовательности Решение.
Тогда по свойству предела частного последовательностей 14 Предельный переход в равенствах и неравенствах Утверждения 8. Теоремы о предельном переходе в равенствах и неравенствах: 1. Если
2. Если
3. Если
Умения 1. Найти предел последовательности
Решение. Очевидно, что при n, стремящемся к бесконечности, последовательности
2. Может ли предел последовательности Решение.
Таким образом, по свойству (1), 15 Нахождение предела последовательности, заданной рекуррентным соотношением К сожалению, общего алгоритма решения не существует, к каждой конкретной ситуации приходится подбирать свое решение, но рассмотрим несколько возможных примеров
Умения 1. Найти предел последовательности Решение. Распишем формулу n-го члена
Тогда (
2. Сходится ли последовательность Решение. Распишем формулу для xn, Тогда Предел не является конечным, то есть данная последовательность расходится. 3. Дана последовательность Решение. Выразим через рекуррентную формулу
Выразим
… Формула общего члена данной последовательности будет иметь вид:
Пределчисловой последовательности равен 16 Раскрытие неопределенностей вида Чаще всего для раскрытия неопределенностей применяются различные алгебраические преобразования. Также полезно знать, что
Где Умения 1.Найти предел последовательности
Поиск по сайту: |








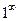
 является общим членом числовой последовательности, заданной функцией
является общим членом числовой последовательности, заданной функцией  .
. .
. . А график представляет собой отдельные точки вида
. А график представляет собой отдельные точки вида  , где k натуральное.
, где k натуральное. ?
?  при
при  .
. числовой последовательностью?
числовой последовательностью? , то получим, что для этой последовательности n не является натуральным, следовательно, она не является числовой последовательностью.
, то получим, что для этой последовательности n не является натуральным, следовательно, она не является числовой последовательностью.



 первый вариант ответа нам не подходит, так как получаем 1, а у нашей последовательности первый член равен 0.
первый вариант ответа нам не подходит, так как получаем 1, а у нашей последовательности первый член равен 0. второй вариант нас не удовлетворяет, так как получаем
второй вариант нас не удовлетворяет, так как получаем 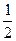 , а второй член нашей последовательности равен 1.
, а второй член нашей последовательности равен 1. четвертый вариант ответа не подходит нам, так как получаем 3, а в нашей последовательности третий член равен 2.
четвертый вариант ответа не подходит нам, так как получаем 3, а в нашей последовательности третий член равен 2.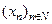 , где
, где  , x1=2.
, x1=2. .
. .
. , x1=1 будет
, x1=1 будет  .
. , верно.
, верно. условие выполняется, то есть
условие выполняется, то есть  .
.
 .
.
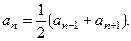
 :
:
 :
:
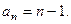
 ограниченна снизу
ограниченна снизу  ; числовая последовательность
; числовая последовательность  .
. ; Числовая последовательность неограниченна сверху
; Числовая последовательность неограниченна сверху  .
. .
.
 ?
? ?
?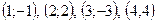 и т.д. То есть несложно заметить, что при нечетных k последовательность уходит в минус бесконечность, а при четных в плюс бесконечность. Ни сверху, ни снизу мы ее ограничить никаким числом не можем, следовательно, данная последовательность неограниченная.
и т.д. То есть несложно заметить, что при нечетных k последовательность уходит в минус бесконечность, а при четных в плюс бесконечность. Ни сверху, ни снизу мы ее ограничить никаким числом не можем, следовательно, данная последовательность неограниченная.

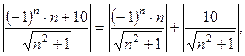

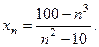


 последовательность является бесконечно большой, а
последовательность является бесконечно большой, а 
 ,
, .
.

 достаточно много раз, мы превысим любое заранее заданное число.
достаточно много раз, мы превысим любое заранее заданное число.

 , где
, где  – период, k любое натуральное число.
– период, k любое натуральное число. ?
?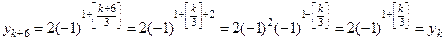 . Итак, мы подтвердили, что последовательность является периодической и ее период равен 6.
. Итак, мы подтвердили, что последовательность является периодической и ее период равен 6. .
. .
. , то есть периодом действительно является 6.
, то есть периодом действительно является 6.
 является периодической, имеет период 1:
является периодической, имеет период 1: 
 ,
, 

 . (1)
. (1) бесконечно малой?
бесконечно малой? . То есть,
. То есть,  .
. , удовлетворяющее условию (1), значит, наша последовательность является бесконечно малой.
, удовлетворяющее условию (1), значит, наша последовательность является бесконечно малой. ?
? . Все члены последовательности опять положительны, поэтому можно их рассматривать без модуля.
. Все члены последовательности опять положительны, поэтому можно их рассматривать без модуля.  . При маленьких ε, 2-3ε будет больше 0, то есть
. При маленьких ε, 2-3ε будет больше 0, то есть  . Значит, при таких ε мы не можем брать n, которые больше
. Значит, при таких ε мы не можем брать n, которые больше  , то есть для таких ε условие (1) не выполняется, так как мы не сможем найти
, то есть для таких ε условие (1) не выполняется, так как мы не сможем найти  . Значит, она не является бесконечно малой.
. Значит, она не является бесконечно малой. .
.


 .
.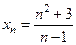 является бесконечно большой.
является бесконечно большой.  .
.
 дискриминант меньше 0, то есть все члены последовательности удовлетворяют условию. Теперь пусть
дискриминант меньше 0, то есть все члены последовательности удовлетворяют условию. Теперь пусть  . Тогда
. Тогда  , то есть можно взять
, то есть можно взять  . Таким образом, для всех положительных n мы нашли
. Таким образом, для всех положительных n мы нашли  .
.
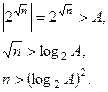

 , данная числовая последовательность будет являться бесконечно большой.
, данная числовая последовательность будет являться бесконечно большой. является бесконечно малой последовательностью.
является бесконечно малой последовательностью. .
. ?
? является бесконечно малой последовательностью, т.к.
является бесконечно малой последовательностью, т.к.  , то есть
, то есть  . А sinn последовательность ограниченная, следовательно, по свойству (5) последовательность
. А sinn последовательность ограниченная, следовательно, по свойству (5) последовательность  ?
? являются бесконечно малыми последовательностями (из предыдущих примеров), а значит по свойству (3) их разность будет тоже являться бесконечно малой последовательностью.
являются бесконечно малыми последовательностями (из предыдущих примеров), а значит по свойству (3) их разность будет тоже являться бесконечно малой последовательностью. является бесконечно малой, то что можно сказать о последовательности
является бесконечно малой, то что можно сказать о последовательности  является бесконечно большой и наоборот.
является бесконечно большой и наоборот. ?
? .
. - бесконечно малая последовательность,
- бесконечно малая последовательность,  - ограниченная, то есть их произведением будет являться бесконечно малая последовательность. Но так как мы рассматриваем
- ограниченная, то есть их произведением будет являться бесконечно малая последовательность. Но так как мы рассматриваем  .
. сходится и найти ее предел.
сходится и найти ее предел.  бесконечно малая.
бесконечно малая. .
.  – бесконечно большая, значит,
– бесконечно большая, значит,  будет бесконечно малой, и
будет бесконечно малой, и  тоже. Таким образом, 1 является пределом числовой последовательности
тоже. Таким образом, 1 является пределом числовой последовательности  и
и  . Их пределы соответственно равны 1, 5, 4. Что можно сказать о последовательности
. Их пределы соответственно равны 1, 5, 4. Что можно сказать о последовательности 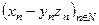 ?
?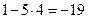 .
.
 - бесконечно малая последовательность, то есть ее предел равен 0.
- бесконечно малая последовательность, то есть ее предел равен 0. , предел
, предел  равен 0, так как она тоже является бесконечно малой. И, наконец, предел
равен 0, так как она тоже является бесконечно малой. И, наконец, предел  равен 4. Таким образом, получаем, что предел
равен 4. Таким образом, получаем, что предел  .
. имеет пределы 1 и -1?
имеет пределы 1 и -1?
 , нам необходимо рассмотреть пределы при
, нам необходимо рассмотреть пределы при  и
и  ,
, 





 , где
, где 
 , где
, где 
 , где
, где 
 , где
, где  попадают в ε-окрестность 3, при
попадают в ε-окрестность 3, при  .
.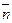 , который удовлетворяет условию
, который удовлетворяет условию 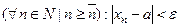 ,где а – это число, в ε- окрестность которого должны попадать все члены последовательности
,где а – это число, в ε- окрестность которого должны попадать все члены последовательности 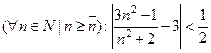 . Итак,
. Итак,
 . Значит,
. Значит,  попадают в ε-окрестность +
попадают в ε-окрестность +  .
. , ε>0.
, ε>0. .
.
 , то есть
, то есть  , ε>0)
, ε>0) попадают в ε-окрестность
попадают в ε-окрестность  .
. , ε>0.
, ε>0. .
.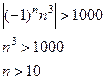


 -окрестности
-окрестности  .
.


 последовательность будет попадать в
последовательность будет попадать в  .
.





 последовательность будет попадать в
последовательность будет попадать в  .
.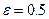 либо четные, либо нечетные члены последовательности не будут попадать в ε-окрестность числа а), то есть она не является сходящейся.
либо четные, либо нечетные члены последовательности не будут попадать в ε-окрестность числа а), то есть она не является сходящейся. будет последовательность
будет последовательность  .
. .
. .
. , естественно при условии, что никакое из
, естественно при условии, что никакое из  не равно 0.
не равно 0. ,
,  , то
, то  сходится и
сходится и 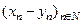 сходится и
сходится и  .
. сходится и
сходится и  .
. , то
, то  сходится и
сходится и  .
. .
.
 .
. .
.  .
. .
. ;
;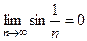 , по свойству предела суммы последовательностей
, по свойству предела суммы последовательностей  .
. .
. , тогда
, тогда  .
. , тогда
, тогда  .
. , тогда
, тогда 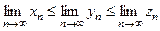 .
. .
. и
и  стремятся к 0. Но из свойства (3)
стремятся к 0. Но из свойства (3) 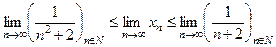 , то есть
, то есть , значит,
, значит,  .
. быть больше чем 3?
быть больше чем 3? .
. . Значит, предел этой последовательности не может быть больше 3.
. Значит, предел этой последовательности не может быть больше 3. , а
, а  .
.
 .
. равен 1, так как каждый раз при увеличении n мы уменьшаем расстояние между xn и 1 ровно в половину. Мы будем бесконечно приближаться к 1, но никогда ее не достигнем.)
равен 1, так как каждый раз при увеличении n мы уменьшаем расстояние между xn и 1 ровно в половину. Мы будем бесконечно приближаться к 1, но никогда ее не достигнем.)

 определяется формулами
определяется формулами  ,
, 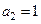 ,
,  . Найти
. Найти  .
.
 .
.
 и
и 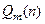 многочлены степени k и m соответственно, а q и p их старшие степени.
многочлены степени k и m соответственно, а q и p их старшие степени.