 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Графическое изображение вариационных рядов
Графическое изображение зависимости между величинами дает возможность представить ее наглядно. Для изображения вариационных рядов, т.е. соотношений между значениями признака и соответствующими частотами или относительными частотами, являются полигон, гистограмма и кумулята. Их построения выполняют в программе Microsoft Excel. Полигон чаще всего используют для изображения дискретных рядов. Для построения полигона в прямоугольной системе координат в произвольно выбранном масштабе на оси абсцисс откладывают значения аргумента, т. е. варианты, а на оси ординат – значения частот или относительных частот. Масштаб выбирают такой, чтобы была обеспечена необходимая наглядность. Полигоном абсолютных частот называют кривую, отрезки которой соединяют точки (а1; р1), (а2; р2), …, (аm; рm). Таблица и полигон абсолютных частот задают эмпирический закон распределения.
Рис. 7.1. Полигон абсолютных частот Полигоном относительных частот называют кривую, отрезки которой соединяют точки (а1; р1*), (а2; р2*), …, (аm; рm*). Таблица и полигон относительных частот задают эмпирический закон распределения.
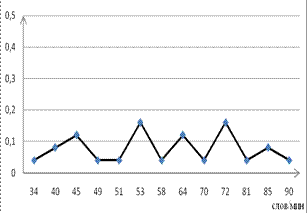
Рис. 7.2. Полигон относительных частот Графики абсолютных и относительных частот не отличаются, разница лишь в том, что полигон абсолютных частот в n раз выше полигона относительных. Поэтому при графическом или табличном представлении первичной обработки выборки можно использовать один из эмпирических законов (либо относительных, либо абсолютных частот). Эмпирический закон распределения в примере 2 наглядно представлен в виде полигонов для абсолютных (рис. 7.3) и относительных (рис. 7.4) частот скорости чтения.
Рис. 7.3
Рис.7.4 Для непрерывных эмпирических переменных, а также для дискретных выборок большого объема используется интервальный закон распределения. При анализе результатов скорости чтения можно не рассматривать в отдельности каждое значение, а разбить их на группы. Ведь сложно отличить скорость 51 от 53 слов/мин, но можно различить учащихся, скорость чтения которых находится в диапазоне от 30 до 50 и от 70 до 90 слов/мин. В литературе описываются различные способы группирования значений и разбиения на интервалы. В школьной практике границы группы часто определяются критериями отметки. Если в интервальном вариационном ряде в двух последовательных интервалах верхнее предельное значение признака одного интервала равно нижнему предельному значению второго, условно считают, что это число принадлежит второму интервалу. Разность между верхней и нижней границами интервала называется шириной этого интервала. Для изображения интервального закона распределения используют гистограмму. Для построения гистограммы по данным вариационного ряда с равными интервалами, как и для полигона, на оси абсцисс откладывают значения аргумента, а на оси ординат – значения частот или относительных частот. Далее строят прямоугольники, основаниями которых служат отрезки оси абсцисс, длины которых равны длинам интервалов – h, а высотами – отрезки, пропорциональные частотам или относительным частотам соответствующих интервалов. В результате получаютступенчатую фигуру в виде сдвинутых друг к другу прямоугольников, площади которых пропорциональные частотам (или относительным частотам). Если интервалы неравные, то на оси ординат следует откладывать в произвольно выбранном масштабе значения плотности распределения (абсолютной или относительной), т.е. высоты прямоугольников должны равняться плотностям соответствующих интервалов. Плотность распределения– это частота, рассчитанная на единицу ширины интервала, т. е. сколько единиц в каждой группе приходится на единицу величины интервала. Представим вариационный ряд (таблица 7.1) в виде интервального ряда с равными интервалами, длины которых равны 15, в таблице 7.4. Таблица 7.4
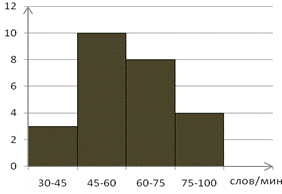
Построим гистограммы частот (рис. 7.5) и относительных часто (рис. 7.6) для рассматриваемой характеристики – скорости чтения.
Рис. 7.5
Рис.7.6 Накопленные частоты определяются путем последовательного суммирования частот по группам и показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение. Для графического изображения вариационных рядов может также использоваться кумулятивная кривая – полигон накопленных частот, при помощи которой изображается ряд накопленных частот (кумулятивный вариационный ряд). Для построения кумуляты на оси абсцисс откладывают значения аргумента, а на оси ординат – накопленные частоты или накопленные относительные частоты. Масштаб для каждой оси выбирают произвольно. Далее строят точки, абсциссы которых равны вариантам (в случае дискретных рядов) или верхним границам интервалов (в случае интервальных рядов), а ординаты – соответствующим частотам (накопленным частотам). Эти точки соединяют отрезками прямой. Полученная ломанная называется кумулятой. По данным таблицы 7.3 составим кумулятивный вариационный ряд для частот (таблица 7.5) и относительных частот (таблица 7.6). Таблица 7.5
Таблица 7.6
По эти данным построим кумуляты для частот (рис. 7.7) и относительных частот (рис. 7.8) скорости чтения учащихся рассматриваемого примера.
Рис. 7.7
Рис. 7.8 Средние величины В результате исследований, связанных с массовыми явлениями, получают много числовых данных. Возникает проблема – найти такие характеристики, которые довольно полно характеризовали бы полученный числовой материал. Характеристики, которые базируются на данных массовых наблюдений, называют обобщающими показателями. Эти показатели характеризуют значения признака, его вариацию. Их вычисляют с помощью вариант и соответствующих частот (относительных частот). Важнейшие среди обобщающих показателей – средние величины, т. е. такие значения признака, вокруг которых группируются отдельные наблюдаемые значения элементов. Отсюда и название – меры центральной тенденции. Средние величины используются для характеристики эмпирического ряда. Они подразделяют на степенные и структурные. К степенным средним величинам относят: арифметическую, геометрическую, гармоническую, квадратичную средние величины. К структурным – моду и медиану. Пусть имеется п объектов, для которых измерена некоторая характеристика, и получены значения x1, x2, …, xn. Средняя степенная отражает величину, варьирующуюся (изменяющуюся) в расчете на единицу всей выборки. Принято различать простые и взвешенные средние величины. Простая средняя величина применяется в тех случаях, когда каждое значение случайной величины встречается один или одинаковое число раз. Если отдельные значения исследуемой выборки встречаются не один, а много, причем неодинаковое число раз, то рассчитывают среднюю взвешенную величину. Простая средняя арифметическая
Взвешенная средняя арифметическая
где pi – абсолютная частота появления значения аi; m — количество различных значений, которые принимает признак. Среднее взвешенное можно интерпретировать как среднюю величину для значений а1, а2, …, ат, используемую в ситуациях, когда одни значения более важны по сравнению с другими. Чем больше частота элемента, тем больший вклад вносит этот элемент в значение среднего взвешенного. Среднее взвешенное можно использовать для оценки неизвестных параметров совокупности, для решения задач, связанных с проверкой гипотез. Пример 3. Два стрелка сделали по 100 выстрелов. Первый выбил 8 очков 40 раз, 9 очков – 10 раз и 10 очков – 50 раз. Второй выбил 8, 9 и 10 очков соответственно – 10, 60 и 30 раз. Какой из стрелков стреляет лучше? Решение. Вычислим средние взвешенные арифметические
Среднее число очков, которое выбивает из 100 выстрелов второй стрелок, несколько выше, чем тот же показатель у первого стрелка. Естественно признать второго стрелка лучшим. Среднее гармоническое необходимо в том случае, когда наблюдения, для которых мы хотим получить среднее арифметическое, заданы обратными значениями. В общем случае среднее гармоническое значений x1, x2, …, xn определяется по формулам
Средняя гармоническая взвешенная
Средняя гармоническая простая применяется в тех случаях, когда произведения Пример 4. Первую половину пути турист двигался со скоростью 4 км/ч, а вторую половину – со скоростью 6 км/ч. Какова средняя скорость движения туриста на протяжении всего пути?
При определении коэффициента среднего темпа роста, когда необходимо сохранить неизменным произведение каждой величины признака, применят простую геометрическую Среднее геометрическое значение x1, x2, …, xn определяется по формулам:
Среднее геометрическое используют прежде всего тогда, когда среднее значение вычисляют для значений, заданных через некоторые равные промежутки времени (рост или снижение успеваемости, вклада в банке за несколько лет и др.); когда переменная с течением времени изменяется примерно с одинаковым соотношением между измерениями, когда отдельные значения в статистической совокупности удалены от других значений. Среднее степенное k-го порядка определяется по формулам
Среднее степенное второго порядка называют средним квадратичным. Среднее арифметическое является степенным средним порядка 1, среднее гармоническое – порядка (–1).
Средняя квадратичная применяется, когда осреднению подлежат величины, выраженные в виде квадратичных функций. Между величинами степенных средних, рассчитанных по одной и той же совокупности единиц статистического наблюдения и одному и тому же признаку, существует следующее соотношение: Структурные средние величины используются для характеристики центральной тенденции изменяющейся случайной величины, уровень случайной величины. Медиана (Me) – значение случайной величины в ранжированном вариационном ряду, делящая его на две равные части. Медиана обладает важными свойствами, которые в некоторых случаях дают ей преимущество перед другими средними величинами. Например, если при упорядоченном размещении некоторого признака «крайние» значения сомнительные и к тому же резко отличаются от основной массы данных, то в качестве меры центральной тенденции целесообразно использовать медиану, так как на ее величину эти «крайние» значения никакого влияния не оказывают, и в то же время они могут существенным образом повлиять на значение среднего арифметического. При нахождении медианы дискретного вариационного ряда следует различать два случая, когда объем совокупности: 1) нечетный; 2) четный. Если объем совокупности нечетный и равен 2п + 1, и варианты размещены в порядке возрастания их значений:
то Ме = хп + 1 (7.14). Если же количество элементов четное и равно 2п, то нет варианты, которая бы делила совокупность на две равные по объему части:
Поэтому в качестве медианы условно берется полусумма вариант, находящихся в середине вариационного ряда:
Мода (Mo) – называют наиболее часто встречающееся значение случайной величины в эмпирическом ряду. Если все значения в вариационном ряде встречаются одинаково часто, то считают, что этот ряд не имеет моды. Если два соседних значения вариационного ряда имеют одинаковую частоту и она больше частоты любого другого значения, то считают, что мода равняется среднему арифметическому этих значений. Если два не соседних значения вариационного ряда имеют одинаковую частоту и она больше частоты любого другого значения, то считают, что вариационный ряд имеет две моды, а соответствующее распределение называют бимодальным. Пример 5. Для нахождения медианы необходимо составить ранжированный вариационный ряд: 34, 40, 40, 45,45,45,49,51, 53, 53, 53, 53, 58, 64, 64, 64 70, 72,72,72,72, 81, 85, 85, 90. Общее количество элементов – 25, число нечетное, поэтому медиана равна числу 58 , которое стоит посередине (на 13-м месте). Для нахождения моды удобно использовать представление выборки в виде дискретного вариационного ряда (Таблица 7.3). Из таблицы видно, что два не соседних значения вариационного ряда (72 и 53) имеют одинаковую наибольшую частоту 4, значит рассматриваемый ряд – бимодальный. Показатели вариации Вариация – различия (изменчивость) в значениях признака данной генеральной совокупности. Показатель вариации – числовая характеристика колебания значений случайной величины. Часто бывает важно знать не только «среднее», наиболее часто встречающееся значение в наборе чисел, но и иметь представление о том, насколько элементы выборки отличаются друг от друга или от среднего значения выборки. Размах вариации (R) показывает, в каких пределах колеблется размер признака, образующего эмпирический ряд: R = xmax – xmin. (7. 16) Размах показывает насколько велико рассеивание значений в выборке. Генеральной средней называетсявзвешенная средняя арифметическаядискретного вариационного ряда для генеральной совокупности, выборочная средняя – взвешенная средняя арифметическаявыборки. Отклонение характеризует расположение значений выборки по отношению к ее средней (генеральной или выборочной). Если число меньше среднего, то его отклонение отрицательно; если число больше среднего, то отклонение положительно. Пример 6. Дан набор чисел: 1, 6, 7, 9, 12. Среднее арифметическое равно (1+6+7+9+12) : 5=7 Отклонения: 1 – 7=–6; 6 – 7=–1; 7 – 7=0; 9 – 7=2; 12 – 7=5. Набор отклонений от среднего арифметического является наиболее полной характеристикой разброса чисел. По нему можно судить о том, насколько разнообразны числа в выборке. Если отклонения малы, то числа в выборке расположены близко к среднему арифметическому. Для любой выборки сумма всех отклонений равна 0. В примере 6: – 6 – 1 + 0 + 2 + 5=0. Для большой выборки рассматривать набор отклонений практически неудобно. Надо описать разнообразие чисел в наборе одной характеристикой, одним числом. Размах – слишком грубая мера разброса чисел в выборке; среднее отклонений равно нулю и его нельзя использовать как меру разброса. Поэтому принято складывать не сами отклонения, а их квадраты. Чем больше отклонения от среднего арифметического, тем больше сумма их квадратов. Среднее арифметическое квадратов отклонений значения вариации от среднего значения называется генеральной или выборочной дисперсией (D) (для генеральной совокупности или выборки соответственно): Dг или Dв.
Для рассматриваемого набора чисел (пример 6):
Под первичной обработкой данных будем понимать построение: 1) ранжированного вариационного ряда; 2) таблицы абсолютных и относительных частот; 3) таблицы накопленных частот; 4) таблицы интервального закона распределения; 5) полигона абсолютных или относительных частот; 6) полигона накопленных частот; 7) гистограммы; а также вычисление: 8) средней степенной величины, наиболее уместной для условий выборки; 9) моды и медианы; 10) абсолютных и относительных показателей вариации. Для обработки статистических данных можно использовать статистические функции программы Microsoft Excel. Контрольные вопросы 1. Что такое генеральная совокупность; признак генеральной совокупности; выборка? 2. Что показывает частота значения? 3. Как построить ранжированный ряд; дискретный ряд? 4. Что показывает относительная частота значения? 5. Что показывает ранг объекта? Как подсчитывается ранг объекта? 6. Какие виды табличного и графического представления данных первичной обработки существуют? 7. Какие средние величины существуют, каким образом они находятся? 8. Как найти абсолютные и относительные показатели вариации? 9. Что понимают под первичной обработкой данных? ЛАБОРАТОРНАЯ РАБОТА «Обработка данных в электронных таблицах программы Microsoft Excel». Задача 1. Составьте таблицу и произведите расчет стоимости 100 г салата, для которого необходимы следующие продукты: картофель – 0,6 кг по 20 руб. за килограмм, колбаса – 500 г по 250 руб., огурцы – 0,3кг по 50 руб., зеленый горошек – 1 банка массой 300 г за 40 руб. и зелень – 0,1кг за 400 руб.
Задача 2. Ученики 5 класса купили школьные принадлежности по следующей цене: тетрадь – 5 рублей, ручка – 8 рублей, карандаш – 7 рулей, ластик – 4 рубля. Валя – 2 тетради, 3 ручки, 1 карандаш, 4 ластика Юра – 1 тетрадь, 2 ручки, 4 карандаша, 2 ластика Костя – 3 тетради, 5 ручек, 2 карандаша, 1 ластик Марина – 3 тетради, 2 ручки, 2 карандаша,1 ластик Валя – 2 тетради, 3 ручки, 1 карандаш, 4 ластика Света – все предметы по 2 штуки. Задание: 1) Составьте таблицу к этой задаче. 2) Найдите стоимость покупки каждого из ребят. 3) Найдите общую стоимость покупки. 4) Кто из ребят истратил больше денег на покупку? Задача 3. Составьте таблицу для решения следующей задачи. Известны фамилии абитуриентов и результаты экзаменов.
1) Определите сумму баллов у каждого абитуриента. 2) Составьте список абитуриентов в порядке убывания. 3) Определите, будет ли он принят в университет, если известен проходной балл – 170. 4) Определите количество зачисленных в университет. 5) Определите средний балл по каждому предмету. 6) Составьте диаграмму для средних баллов. Задача 4. Известны фамилии студентов и результаты теста в баллах: Бобров – 72, Орехова – 37, Снегирева – 47, Петров – 54, Смирнова – 24, Симонова – 92, Орлова – 67, Шевелева – 17, Кривко – 81, Антонов – 62, которые необходимо перевести в отметку: «5» – не меньше 80 баллов; «4» – не меньше 60, но меньше 80 баллов; «3» – не меньше 30, но меньше 60 баллов; «2» – меньше 30 баллов. Составьте таблицу для решения следующей задачи. 1) Определите отметку каждого студента. 2) Определите, сколько человек получили 5, 4, 3 и 2. 3) Отобразить этот результат в виде графика успеваемости и круговой диаграммы.
Поиск по сайту: |






 – сумма всех значений выборки, деленная на общее количество этих значений:
– сумма всех значений выборки, деленная на общее количество этих значений: . (7.6)
. (7.6) – средняя из вариант (аi) дискретного вариационного ряда, которые повторяются различное количество раз или имеют разный вес, находится следующим образом:
– средняя из вариант (аi) дискретного вариационного ряда, которые повторяются различное количество раз или имеют разный вес, находится следующим образом: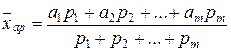 , (7.7)
, (7.7) и
и  числа очков, которые выбил при 100 выстрелах каждый из двух стрелков.
числа очков, которые выбил при 100 выстрелах каждый из двух стрелков.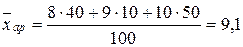 ;
;  .
. или
или  . (7. 8)
. (7. 8) вычисляется, когда нет информации о частоте варианта выборки, а известно их произведение
вычисляется, когда нет информации о частоте варианта выборки, а известно их произведение  :
: . (7. 9)
. (7. 9) одинаковы или равны 1.
одинаковы или равны 1. ;
; 
 и взвешенную геометрическую
и взвешенную геометрическую 
 и
и  . (7.10)
. (7.10)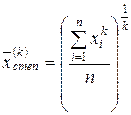 или
или  . (7.11)
. (7.11)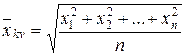 – простая квадратичная; (7.12)
– простая квадратичная; (7.12) – взвешенная квадратичная. (7.13)
– взвешенная квадратичная. (7.13) .
.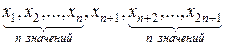 ,
, .
.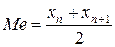 . (7. 15)
. (7. 15) . (7.17)
. (7.17) .
.