 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Непрерывность функции в точке. Классификация точек разрыва ⇐ ПредыдущаяСтр 3 из 3
Функция 1) функция 2) существует 3) На e-языке это определение можно записать следующим образом:
Необходимое и достаточное условие непрерывности функции Итак, функция непрерывна в точке, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. Если в точке а) б) если существуют односторонние пределы в) в остальных случаях Свойства функций, непрерывных в точке Если функции Все многочлены являются непрерывными функциями во всех точках числовой прямой. Всякая элементарная функция непрерывна во всех точках, в которых она определена (элементарной функцией называется функция, которая может быть выражена через функции С (С – константа), Замечание. Поскольку Пример. Доказать, что функция Решение. Проверим необходимое и достаточное условие непрерывности:
Найти точки разрыва функции
Решение. Функция имеет разрыв в точке
Эти пределы не равны. Следовательно, точка Пример. Найти точки разрыва функции Решение. Функция имеет разрыв в точке
Эти пределы равны, следовательно, точка Пример. Найти точки разрыва функции Решение. Точка
Заметим, что второй односторонний предел конечен Задачи. Доказать, что следующие функции непрерывны в каждой точке своей области определения: 6.95. 6.97. 6.99. 6.101. Найти точки разрыва функции, исследовать их характер, в случае устранимого разрыва доопределить функцию до непрерывной: 6.103. 6.105. 6.107. 6.109. 6.111. Исследовать на непрерывность функции: 6.113. Исследовать на непрерывность и построить график функции 6.115. 6.117. 6.118.
Поиск по сайту: |
 с областью определения D называется непрерывной в точке
с областью определения D называется непрерывной в точке 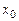 , если выполнены следующие три условия:
, если выполнены следующие три условия: ;
; ;
; .
. .
. .
. и
и  , но
, но  , то
, то 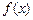 и
и  непрерывны в точке
непрерывны в точке  , разность
, разность  , произведение
, произведение 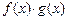 , а также частное
, а также частное  при условии, что
при условии, что  .
. с помощью арифметических действий и образования сложной функции).
с помощью арифметических действий и образования сложной функции). , то
, то  , т.е. для непрерывной функции символы предела и функции перестановочны.
, т.е. для непрерывной функции символы предела и функции перестановочны. является непрерывной.
является непрерывной. Оно выполняется, значит, функция
Оно выполняется, значит, функция  Пример.
Пример.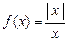 и исследовать их характер.
и исследовать их характер. , т.к. в этой точке она не определена (рис.14). Найдем односторонние пределы:
, т.к. в этой точке она не определена (рис.14). Найдем односторонние пределы: .
. и исследовать их характер.
и исследовать их характер. , т.к. в этой точке она не определена. Найдем односторонние пределы, используя первый замечательный предел:
, т.к. в этой точке она не определена. Найдем односторонние пределы, используя первый замечательный предел: .
. .
. и исследовать их характер.
и исследовать их характер. .
. .
. ; 6.96.
; 6.96. 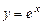 ;
; ; 6.98.
; 6.98.  ;
; ; 6.100.
; 6.100.  ;
; ; 6.102.
; 6.102.  .
. ; 6.104.
; 6.104.  ;
; ;
; ; 6.108.
; 6.108.  ;
;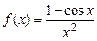 ; 6.110.
; 6.110. 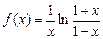 ;
;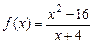 ; 6.112.
; 6.112.  .
. 6.114.
6.114. 
 6.116.
6.116. 

