 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Общие теоретические сведенияСтр 1 из 2Следующая ⇒
Тема 3. ИСПОЛЬЗОВАНИЕ ЭЛЕМЕНТОВ ТЕОРИИ МНОЖЕСТВ ДЛЯ РАБОТЫ С ИНФОРМАЦИЕЙ Задания и вопросы для подготовки к занятию: 1. Вспомните условное обозначение и состав основных числовых множеств, изучаемых в школьном курсе математики: множество натуральных чисел, множество целых чисел, множество рациональных чисел, множество действительных чисел. 2. Выясните, кто являлся создателем теории множеств. 3. Исключите лишние элементы из последовательностей. Обоснуйте свой выбор: - Булгаков, Есенин, Лермонтов, Пушкин, Толстой, Шекспир; - Прыжки в длину, в высоту, с десятиметровой вышки, тройной прыжок; - Клубника, арбуз, вишня, яблоко, смородина; - 22, 17, 180, 25006, 6, 84. Общие теоретические сведения Одним из фундаментальных математических понятий является понятие множества. Множество – первичное понятие математики, т.е. это понятие не определяется через другие, а только поясняется. Множество можно представить себе как соединение, совокупность, собрание некоторых предметов, объединенных по какому-либо признаку. Например, множество учащихся класса, множество букв алфавита, множество натуральных чисел, множество точек на прямой, множество книг на полке. Для названия множества иногда используют какое-либо одно слово, выступающее в роли синонима слова «множество» (зрители, семья, деревья). Обозначают множества заглавными буквами латинского алфавита (A, B, C) или символически с помощью фигурных скобок, в которых указываются его элементы: Принадлежность предмета некоторому множеству обозначают с помощью символа Запись Основными способами задания множества являются: 1) перечисление всех его элементов: 2) описание (указание характеристического свойства его элементов). Этот способ требует указания такого признака, который имеется у всех элементов данного множества и не свойственен элементам, не входящим в данное множество. Например, множество «хор» можно охарактеризовать как множество людей (или птиц), поющих вместе. Говоря о множестве четных чисел, мы указываем характеристическое свойство его элементов: Элементы конечного множества можно перечислить, а элементы бесконечного множества даже теоретически нельзя собрать в законченную совокупность. Конечные множества можно задать как перечислением, так и с помощью характеристического свойства. Бесконечные множества задаются только с помощью характеристического свойства. Мощность конечного множества – это количество элементов, которые принадлежат данному множеству, обозначается как m(A), что означает мощность множества А. Например, если Множество, которое не содержит ни одного элемента, называется пустым и обозначается символом Ø. Мощность пустого множества равна 0. Множество В, состоящее из некоторых элементов данного множества А (и только из них), называется подмножеством (частью) этого множества. Иначе, если любой элемент множества В принадлежит также множеству А, то множество В называется подмножеством множества А. Это записывается так: Знак « Например, множество целых чисел Если в множестве В найдется хотя бы один элемент, не принадлежащий множеству А, то В не является подмножеством множества А: Множества А и В называют равными ( В каждом отдельном случае мы рассматриваем всевозможные подмножества одного и того же множества. Например, в начальной школе дети учатся работать (выполнять основные арифметические операции) сначала с числами из первого десятка натуральных чисел, затем из первой сотни и т.д. Но их действия не выходят за рамки натуральных чисел (отрицательные и дробные числа они будут проходить позже). Аналогично, учитель может работать с некоторыми группами учеников, которые будут являться подмножествами определенного множества обучаемых данным учителем школьников. Это основное множество (свое в каждом отдельном случае) называется универсальным множеством. Универсальным множеством (обозначается U) называется множество, подмножества которого (и только они) в данный момент рассматриваются. При работе с числовыми множествами, если не дается дополнительных указаний, в качестве основного (универсального) множества будем считать множество R действительных чисел. Для наглядного представления (графического изображения) множеств и результатов операций над ними удобно пользоваться так называемыми диаграммами Эйлера-Венна (кругов Эйлера). На диаграммах Эйлера-Венна множества изображаются на плоскости в виде замкнутых кругов, а универсальное множество в виде прямоугольника. Элементы множества – точки внутри соответствующего круга (рис.1).
Рис.1 Если множество В является подмножеством А, то круг, изображающий множество В, целиком помещается в круг, изображающий множество А (рис.2). Равные множества представляют в виде одного круга (рис.3).
В математике часто приходится решать задачи, которые связаны с нахождением общих элементов двух или более совокупностей или с объединением нескольких совокупностей в одну. Такие преобразования называются операциями над множествами. Например, А – множество наклеек (марок), которые есть у Пети, В – множество наклеек, которые собрал Вася. Можно выделить множество наклеек, которые есть у обоих ребят; коллекцию различных наклеек, собранных ими вместе; множество наклеек Пети, которых нет у Васи. Таким образом, мы проделали операции пересечения, объединения и разности двух множеств. Объединением (суммой) множеств Например, даны множества Если представить множества А и В при помощи кругов Эйлера, то объединение данных множеств изобразится закрашенной областью (рис.4). Пересечением (произведением) множеств Для множеств Множества, не имеющие общих элементов
Естественно поставить вопрос о нахождении числа элементов в объединенном множестве С. Если множества А и В не содержат одинаковых элементов, то В противном случае, когда множества имеют
Разностью множеств А \ В называется множество С, состоящее из всех элементов множества А, не принадлежащих множеству В. Например, даны множества Обратим внимание, что разность На рис. 6-7 представлены диаграммы Эйлера-Венна для операции разности множеств.
В случае, когда В является подмножеством А, т.е.
Рис.8 Операции над множествами обладают следующими основными свойствами: коммутативности (для операций объединения и пересечения), ассоциативности (для операций объединения и пересечения), дистрибутивности (операции пересечения относительно объединения и операции объединения относительно пересечения). Одним из способов конструирования новых объектов из уже имеющихся множеств является декартово произведение множеств. Рассмотрим следующую ситуацию. Фабрика детских игрушек выпускает плюшевых мишек, зайцев, собак, слонов следующих расцветок: розовый, синий, жёлтый, зеленый, коричневый. Обозначим через А множество видов изделий: А = {медведь, заяц, собака, слон}, через В – множество предлагаемых расцветок: В = {розовый, синий, жёлтый, зеленый, коричневый}. Посмотрим, какие игрушки можно получить, учитывая возможные для них расцветки. Для этого составим список всех пар из элементов множества А и элементов множества В таким образом, что сначала будем записывать элемент множества А, затем элемент множества В. Получим множество С упорядоченных пар элементов множеств А и В. Возможные изделия можно перечислить с помощью таблицы. Итак, мы имеем дело с особым множеством, составленным из элементов двух данных множеств. Такое произведение называется декартовым произведением двух множеств.
Декартовым (или прямым) произведением множества А на множество В называется множество всех упорядоченных пар, в которых первая компонента – элемент множества А, а вторая – элемент множества В. Обозначают Таким образом, Для описания прямого произведения множеств бывает удобно использовать «геометрический язык». При этом элементы множества
Рис.9. Для нахождения общего числа элементов в декартовом произведении двух множеств можно воспользоваться следующим соотношением: если В математике большую роль играет теория отношений, которая оказалась простым и удобным аппаратом для самых разнообразных задач. На ее основе обобщается понятие функции, применимое не только к числовым множествам, но и к множествам объектов любой природы. В самом общем смысле отношение означает какую-либо связь между предметами или понятиями. Центральное место занимают бинарные отношения – отношения, заданные на декартовом произведении двух множеств. Особо выделяются три типа бинарных отношений: эквивалентность, упорядоченность и толерантность, которые наиболее часто встречаются в практике. Примеры решения основных типов задач Пример 1. Способы задания множеств. Определить способ задания множества А = {Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун, Плутон}. Перейти к другому способу, если это возможно. Определить мощность множества. Решение. а) Перечислены все элементы множества А, следовательно, множество задано перечислением. б) Любое множество можно задать с помощью характеристического свойства. Общим свойством элементов данного множества А является то, что все они буквы русского алфавита. Следовательно, с помощью характеристического свойства множество представимо как в) Общее число элементов множества А, множества планет Солнечной системы, равно 9, поэтому его мощность m (A) = 9. Пример 2. Отношения между множествами. Сравнить множество А с множествами B, C, D. Если множества пересекаются, найти их пересечения. Найти универсальное множество для данных множеств. Изобразить отношения между множествами с помощью диаграмм Эйлера-Венна. А = {красный, желтый, синий, зеленый}. B = {красный, желтый}. С = {желтый, синий, черный, оранжевый}. D = {коричневый, голубой, розовый}. Решение. Все элементы множества В содержатся во множестве А, но невсе элементы множества А являются элементами множества, поэтому U = {множество цветов}.
Пример 3. Операции над множествами. Даны множества А = {2, 3, 5, 8, 13, 15}, В= {1, 3, 4, 8,16}, С= {12, 13, 15, 16}, D = {0, 1, 20}. Найти Решение. Будем пользоваться определениями соответствующихопераций и учтем, что сначала должна выполняться операция пересечения множеств, а затем уже объединение или разность. Получим:
Пример 4. Подсчет количества элементов в объединении, пересечении и разности конечных множеств. В группе из 100 туристов 70 человек знают английский язык, 45 знают французский язык и 23 человека знают оба языка. Сколько туристов в группе не знают ни английского, ни французского языка? Решение. Пусть А – множество туристов, знающих английский язык, В – множество туристов, знающих французский язык. Поусловию m (A) = 70, m (В) = 45. Туристы, знающие оба языка, образуют множество Объединенное множество – число туристов, знающих английский и (или) французский язык, можно найти по формуле:
Туристы, не знающие ни английского, ни французского языка, составляют множество Пример 5. Декартово произведение множеств. Перечислить все элементы декартова произведения множеств Решение. А×В={(-2,-1), (-2,0), (-2,2), (-2,5),(1,-1), (1,0), (1,2), (1,5), (3,-1), (3,0), (3,2),(3,5)}.
Поиск по сайту: |
 . Сами элементы некоторого множества обозначают малыми латинскими буквами, если они не имеют специальных обозначений:
. Сами элементы некоторого множества обозначают малыми латинскими буквами, если они не имеют специальных обозначений:  .
.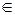 (в противном случае используется символ
(в противном случае используется символ  ).
). означает, что а есть элемент множества А, а выражение
означает, что а есть элемент множества А, а выражение  означает, что элемент а не принадлежит множеству А.
означает, что элемент а не принадлежит множеству А.
 , т.е. каждое число, принадлежащее этому множеству, делится на два.
, т.е. каждое число, принадлежащее этому множеству, делится на два. , то
, то  . Если N – множество всех натуральных чисел, то
. Если N – множество всех натуральных чисел, то  .
. или
или  . Говорят, что «В – подмножество А» или «В содержится в А» или «А содержит В». Заметим, что
. Говорят, что «В – подмножество А» или «В содержится в А» или «А содержит В». Заметим, что 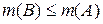 .
. » называется знаком включения.
» называется знаком включения. содержит все натуральные числа и числа, им противоположные
содержит все натуральные числа и числа, им противоположные  .
. .
. ), если
), если  . Например, множества
. Например, множества  и
и  равны, так как состоят из одинаковых элементов.
равны, так как состоят из одинаковых элементов.


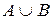 называется множество С, все элементы которого принадлежат множеству А илимножеству В.
называется множество С, все элементы которого принадлежат множеству А илимножеству В. и
и  . Объединением данных множеств является
. Объединением данных множеств является  , т.е.
, т.е.  .
. называется множество C, состоящее из всех тех и только тех элементов, которые принадлежат множеству А и множеству В.
называется множество C, состоящее из всех тех и только тех элементов, которые принадлежат множеству А и множеству В. , т.е.
, т.е.  . Пересечение двух множеств изображают так, как это показано на рисунке 5.
. Пересечение двух множеств изображают так, как это показано на рисунке 5. Ø, называют непересекающимися (расчлененными).
Ø, называют непересекающимися (расчлененными).








 .
. одинаковых элементов, следует пользоваться более общей формулой:
одинаковых элементов, следует пользоваться более общей формулой: .
. , т.е.
, т.е.  .
.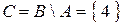 .
.








 и читается «не А» (рис.8).
и читается «не А» (рис.8).
 .
. .
.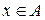
 называется абсциссой, а
называется абсциссой, а  – ординатой точки z. На рис.9 точками показаны элементы декартова произведения множеств
– ординатой точки z. На рис.9 точками показаны элементы декартова произведения множеств  .
.

 , то
, то  .
. .
. {желтый}.
{желтый}.  = Ø.
= Ø.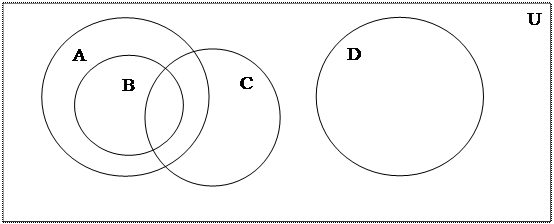
 ,
, 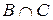 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. ,
,  ,
, ,
,  ,
,  ,
, ,
, 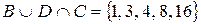 ,
,  .
. .
.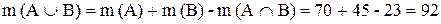 .
. .
.  .
. и
и  .
.