 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
преобразование и построение Матриц ⇐ ПредыдущаяСтр 4 из 4
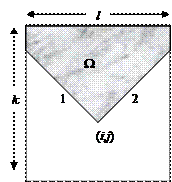
Пусть задана матрица A, размерностью n x n. Необходимо построить матрицу В, причем элементы матрицы строятся по следующей формуле В задачах о выделении областей в матрицах необходимо научиться записывать уравнения изменения индексов при движении по линиям, параллельным главной диагонали, и по линиям, перпендикулярным диагонали. Запишем уравнение линий (1) и (2), проходящих через фиксированную точку (i,j). Пусть изменяемые индексы – l и k. Тогда уравнение прямой (1) (см. рис.1) имеет вид: l = j – i + k, а прямая (2) описывается соотношением: l = j + i - k. Области изменения индексов показаны на рисунке. Если необходимо описать заштрихованную область, то это следует делать так, как это делается при описании областей на плоскости. Легко видеть, что индекс k изменяется в пределах от 1 до i. Индекс l удовлетворяет неравенству 1 £ l £ n. Область выше линии (1) описывается неравенством l > j – i + k, а область выше линии (2) - l < j + i - k. Так как указанная область является пересечением указанных областей, то все перечисленные выше неравенства следует соединять в логическом выражении союзом «и». Таким образом, при построении матрицы В следует воспользоваться четырьмя вложенными циклами, где два внешних описывают индексы матрицы В, то есть изменяются от 1 до n. Что касается двух внутренних циклов, то индекс k изменяется от 1 до i, а индекс l изменяется в пределах от прямой (1) до прямой (2). Ограничения 0 и n следует внести в условие оператора if. Схематически структуру циклов можно изобразить так: i =1 ¸ n j =1 ¸ n k = 1 ¸ i l = j – i + k ¸ j + i – k 1 £ l £ n Конец цикла по l Конец цикла по k Конец цикла по j Конец цикла по i
Программа решения этой задачи и результаты ее выполнения представлены ниже. #include <stdio.h> #include <conio.h> #define m 6 void main() { int i,j,k,l,n; float a[m][m],b[m][m]; clrscr(); gotoxy(5,5); printf("ПРОГРАММА ПОСТРОЕНИЯ МАТРИЦЫ ПО ЗАДАННОЙ"); gotoxy(5,6); printf(" b(i,j)=max a(k,l), k,l принадлежат"); gotoxy(9,7); printf(" заштрихованной области"); gotoxy(35,10); printf("┌ ┐"); gotoxy(35,11); printf("│ * * * * * * * * * * * * * │"); gotoxy(35,12); printf("│ * * * * * * * * * * * * │"); gotoxy(35,13); printf("│ * * * * * * * * * * * │"); gotoxy(35,14); printf("│ * * * * * * * * * │"); gotoxy(35,15); printf("│ * * * * * * * │"); gotoxy(35,16); printf("│ * * * * * │"); gotoxy(35,17); printf("│ * * * │"); gotoxy(35,18); printf("│ * │"); gotoxy(35,19); printf("│ │"); gotoxy(35,20); printf("│ │"); gotoxy(35,21); printf("│ │"); gotoxy(35,22); printf("└ ┘"); getchar();clrscr(); do{ printf("\n\nВведите размерность матрицы <=%d ",m); scanf("%d",&n); }while(!(n>0 && n<=m));clrscr(); for (i=1;i<=n;i++) for (j=1;j<=n;j++){ printf("Введите a(%d,%d)=",i,j);scanf("%f",&a[i-1][j-1]); } clrscr(); printf("ИСХОДНАЯ МАТРИЦА\n"); for (i=1;i<=n;i++){ for (j=1;j<=n;j++) printf("%7.2f",a[i-1][j-1]); printf("\n"); } for (i=1;i<=n;i++) for (j=1;j<=n;j++){ b[i-1][j-1]=-1.e20; for (k=1;k<=n;k++) for (l=j-i+k;l<=j+i-k;l++) if (l>=1 && l<=n && a[k-1][l-1]>b[i-1][j-1]) b[i-1][j-1]=a[k-1][l-1]; } printf("ПОЛУЧЕННАЯ МАТРИЦА\n"); for (i=1;i<=n;i++){ for (j=1;j<=n;j++) printf("%7.2f",b[i-1][j-1]); printf("\n"); } getchar();getchar(); } При выполнении данной программы на экране монитора будет выведено следующее:
ПРОГРАММА ПОСТРОЕНИЯ МАТРИЦЫ ПО ЗАДАННОЙ b(i,j)=max a(k,l), k,l принадлежат заштрихованной области ┌ ┐ │* * * * * * * * * * * * * │ │ * * * * * * * * * * * * │ │ * * * * * * * * * * * │ │ * * * * * * * * * │ │ * * * * * * * │ │ * * * * * │ │ * * * │ │ * │ │ │ │ │ │ │ └ ┘
Введите размерность матрицы <=6 4 Введите a(1,1)= 1.00 Введите a(1,2)= 4.00 Введите a(1,3)= 2.00 Введите a(1,4)= -3.60 Введите a(2,1)= 8.90 Введите a(2,2)= -22.10 Введите a(2,3)= 5.00 Введите a(2,4)= 0.78 Введите a(3,1)= -3.45 Введите a(3,2)= 2.40 Введите a(3,3)= 9.80 Введите a(3,4)= 6.12 Введите a(4,1)= -23.50 Введите a(4,2)= 1.00 Введите a(4,3)= 7.00 Введите a(4,4)= 89.00
ИСХОДНАЯ МАТРИЦА 1.00 4.00 2.00 -3.60 8.90 -22.10 5.00 0.78 -3.45 2.40 9.80 6.12 -23.50 1.00 7.00 89.00
ПОЛУЧЕННАЯ МАТРИЦА 1.00 4.00 2.00 -3.60 8.90 4.00 5.00 2.00 8.90 8.90 9.80 6.12 8.90 9.80 9.80 89.00
Пример 2.
Пусть задана матрица A, размерностью n x n. Необходимо построить матрицу В, причем элементы матрицы строятся по следующей формуле
#include <stdio.h> #include <conio.h> #define m 6 void main() { int i,j,k,l,n; float a[m][m],b[m][m]; clrscr(); gotoxy(5,5); printf("ПРОГРАММА ПОСТРОЕНИЯ МАТРИЦЫ ПО ЗАДАННОЙ"); gotoxy(5,6); printf(" b(i,j)=min a(k,l), k,l принадлежат"); gotoxy(9,7); printf(" заштрихованной области"); gotoxy(35,10); printf("┌ ┐"); gotoxy(35,11); printf("│ │"); gotoxy(35,12); printf("│ * │"); gotoxy(35,13); printf("│ * * │"); gotoxy(35,14); printf("│ * * * │"); gotoxy(35,15); printf("│ * * * * │"); gotoxy(35,16); printf("│ * * * * * │"); gotoxy(35,17); printf("│ * * * * * * │"); gotoxy(35,18); printf("│ * * * * * │"); gotoxy(35,19); printf("│ * * * * │"); gotoxy(35,20); printf("│ * * * │"); gotoxy(35,21); printf("│ * * │"); gotoxy(35,22); printf("│ * │"); gotoxy(35,23); printf("└ ┘"); getchar();clrscr(); do{ printf("\n\nВведите размерность матрицы <=%d ",m); scanf("%d",&n); }while(!(n>0 && n<=m));clrscr(); for (i=1;i<=n;i++) for (j=1;j<=n;j++){ printf("Введите a(%d,%d)=",i,j);scanf("%f",&a[i-1][j-1]); } clrscr(); printf("ИСХОДНАЯ МАТРИЦА\n"); for (i=1;i<=n;i++){ for (j=1;j<=n;j++) printf("%7.2f",a[i-1][j-1]); printf("\n"); } for (i=1;i<=n;i++) for (j=1;j<=n;j++){ b[i-1][j-1]=1.e20; for (l=j;l<=n;l++) for (k=j+i-l;k<=l-j+i;k++) if (k>=1 && k<=n && a[k-1][l-1]<b[i-1][j-1]) b[i-1][j-1]=a[k-1][l-1]; } printf("ПОЛУЧЕННАЯ МАТРИЦА\n"); for (i=1;i<=n;i++){ for (j=1;j<=n;j++) printf("%7.2f",b[i-1][j-1]); printf("\n"); } getchar();getchar();} При выполнении данной программы на экране монитора будет выведено следующее: ПРОГРАММА ПОСТРОЕНИЯ МАТРИЦЫ ПО ЗАДАННОЙ b(i,j)=min a(k,l), k,l принадлежат заштрихованной области ┌ ┐ │ │ │ * │ │ * * │ │ * * * │ │ * * * * │ │ * * * * * │ │ * * * * * * │ │ * * * * * │ │ * * * * │ │ * * * │ │ * * │ │ * │ └ ┘
Введите размерность матрицы <=6 4 Введите a(1,1)= 2.50 Введите a(1,2)= 3.80 Введите a(1,3)=-2.28 Введите a(1,4)= 4.00 Введите a(2,1)= 6.21 Введите a(2,2)= 9.80 Введите a(2,3)=-3.54 Введите a(2,4)= 6.00 Введите a(3,1)= 1.34 Введите a(3,2)= 6.80 Введите a(3,3)=-2.13 Введите a(3,4)= 5.00 Введите a(4,1)= 4.00 Введите a(4,2)= 8.12 Введите a(4,3)= 5.00 Введите a(4,4)= 3.00
ИСХОДНАЯ МАТРИЦА 2.50 3.80 -2.28 4.00 6.21 9.80 -3.54 6.00 1.34 6.80 -2.13 5.00 4.00 8.12 5.00 3.00 ПОЛУЧЕННАЯ МАТРИЦА -3.54 -3.54 -2.28 4.00 -3.54 -3.54 -3.54 6.00 -3.54 -3.54 -2.13 5.00 -3.54 -2.13 3.00 3.00
Эта задача решается с помощью одного основного цикла, в котором организуется управление изменением индексов в зависимости от условий размещения элементов. Для отслеживания направления движения по диагонали вводится вспомогательная переменная l. Ее значение равно 0 при движении вниз по диагонали и 1 при движении вверх.
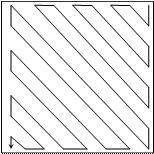
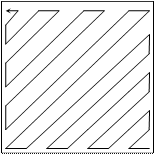
#include<stdio.h> #include<math.h> #include<conio.h> void main() { clrscr(); float p[64]; float a[8][8]; int n=8,i=0,j=0,k,l=0; for (k=0;k<n*n;k++) p[k]=k; for (k=0;k<n*n;k++) { a[i][j]=p[k]; if (j==0 && i<n-1 && l==0 ) { i++ ;l=1; } else if (i==0 && j<n-1 && l==1 ) { j++; l=0;} else if ( j==n-1 && l==1) { i++ ;l=0; } else if (i==n-1 && l==0) { j++; l=1;} else if (l==0) { i++; j--;} else { i--; j++; } } for (i=0;i<n;i++) { for (j=0;j<n;j++) printf("%3.0f ",a[i][j]); printf ("\n"); } } Упражнения 1. Пусть задана матрица A, размерностью n x n. Необходимо построить матрицу В, причем элементы матрицы строятся по следующей формуле 2. Пусть задана матрица A, размерностью n x n. Необходимо построить матрицу В, причем элементы матрицы являются средним значением всех элементов матрицы A в заштрихованной области, где область указана рисунках 1-10. 1. 2.
7. 8.
9. 10.
3. Дан одномерный массив целых чисел А размерностью 64. Получить квадратную матрицу порядка 8 ,элементами которой являются числа массива А, расположенные в ней по схемам, приведенным на рис. 11-17
11 12
13 14
15 16
ЛИТЕРАТУРА
Сборник заданий по вычислительному практикуму на языке Си.
для студентов механико-математического факультета (специальность математика, прикладная математика, механика) Составители Денисов Вадим Вадимович Маркина Марина Викторовна Сабаева Татьяна Анатольевна Савихин Олег Геннадиевич ___________________________________________ Подписано к печати .Формат 60´84 1/16 Печать офсетная. Бумага оберточная. Усл. печ. л. Тираж 300 экз. Заказ .Бесплатно. ____________________________________________________ Нижегородский государственный университет им. Н.И. Лобачевского. 603600 ГСП-20, Н.Новгород, просп. Гагарина, 23. ___________________________________________ Типография ННГУ,603000,Н.Новгород, ул. Б. Покровская 37. ___________________________________________
Поиск по сайту: |
Пример 1.
, где область указана рисунке.
, где область указана рисунке. Область в этом случае следует описать сначала по l, так как этот индекс изменяется в пределах от j до n. Следовательно, внутренние циклы будут: сначала по l от j до n, а затем цикл по k от j+i-l до l-j+i. Так как ищется минимум, то начальное значение следует выбрать достаточно большим. Текст программы и результаты ее работы представлены ниже.
Пример 3. Дан одномерный массив целых чисел Р размерностью 64. Получить квадратную матрицу порядка 8 ,элементами которой являются числа массива Р, расположенные в ней по схеме, приведенной на рисунке.
3. 4.
5. 6.
