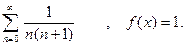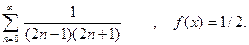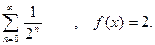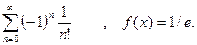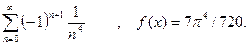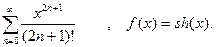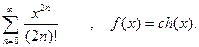|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Позиционная запись числаСтр 1 из 4Следующая ⇒
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Им. Н.И.ЛОБАЧЕВСКОГО МЕХАНИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ
Кафедра теоретической механики Кафедра численного моделирования физико-механических процессов
Сборник заданий по вычислительному практикуму на языке Си.
Методическое пособие
НИЖНИЙ НОВГОРОД
УДК 519.682
Сборник заданий по вычислительному практикуму на языке Си. Методическое пособие / Сост. В.В. Денисов, М.В. Маркина Т.А. Сабаева, О.Г. Савихин. - Н.Новгород: изд-во ННГУ, 2002. - 56 с.
Методическое пособие предназначено для студентов механико-математического факультета и других факультетов ННГУ и призвано оказать помощь в практическом использовании персональных компьютеров в учебном процессе.
Составители: зав. лаб. В.В. Денисов (Глава 1,2), к.ф.-м.н., доцент М.В. Маркина (Глава 3,7), к.ф.-м.н , доцент Т.А. Сабаева (Глава 8), к.т.н., доцент О.Г. Савихин (Глава 3,4,5,6)
Рецензент:
Нижегородский государственный университет им. Н.И. Лобачевского, оглавление
1. Вычисление значений функции.. 3 2. Выделение областей.. 6 3. Суммирование рядов.. 15 4. позиционная запись числа.. 18 5. делители целого числа.. 23 6. преобразование и построение одномерных массивов.. 28 6.1 Линейный поиск в массиве.. 28 6.2 Построение массива без повторений.. 29 7. максимальный и минимальный элементы массива.сортировка 32 8. обработка последовательностей символов.. 39 9. преобразование и построение Матриц.. 41 ЛИТЕРАТУРА.. 55 Вычисление значений функции Пример 1. Вычислить значение функции
#include <stdio.h> #include <math.h> main() {int n; float x; char yn,temp; do { printf("введите n-целое................"); scanf("%i",&n); printf("введите x-десятичное..........."); scanf("%g",&x); if (fabs(x)<5) printf(".........y(%g,%i)=%g\n",x,n,exp(log(log10(26-x*x))/n)); else if ((fabs(x)>5)&&(fabs(x)<sqrt(26))&&(n % 2)) printf(".........y(%g,%i)=%g\n",x,n,-exp(log(-log10(26-x*x))/n)); else if ((fabs(x)==5)&&(n>0)) printf(".........y(%g,%i)=%g\n",x,n,0/n); else printf("Функция не определена\n"); printf("Продолжить работу-y, закончить-n\n"); temp=getchar(); yn=getchar(); temp=getchar(); } while ((yn!='n')&&(yn!='N')); }
Тест:
Упражнения Вычислить значение функции y от x. Значение переменной x и параметров a и b вводить с клавиатуры (Параметр a вещественного типа , параметр b целочисленный, справа от функции даны значения для теста программы): 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25.
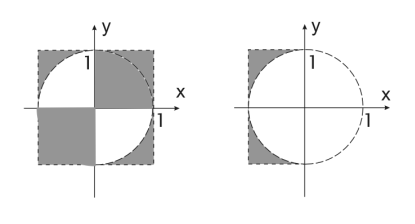
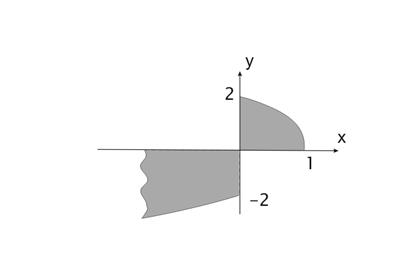
Выделение областей Пример. Определить принадлежность точки с координатами x,y заштрихованной части плоскости:
#include <stdio.h> #include <math.h> #define sq(t) ((t)*(t)) main() {float x,y; char yn,temp; do { printf("введите координату x..............."); scanf("%g",&x); printf("введите координату y..............."); scanf("%g",&y); if (!(x==0)&&(((sq(x-1)+sq(y-1)<=1)&&((y>=x)&&(y>=1/x)|| (y<=x)&&(y<=1/x)))||((sq(x-1)+sq(y-1)>=1)&&((y>=x)&& (y<=1/x)&&(x<0)||(y<=x)&&(y>=1/x)&&(x>0))))) printf("....принадлежит....\n"); else printf("...не принадлежит....\n"); printf("Продолжить работу-y, закончить-n\n"); temp=getchar(); yn=getchar(); temp=getchar(); } while ((yn!='n')&&(yn!='N')); } Тест:
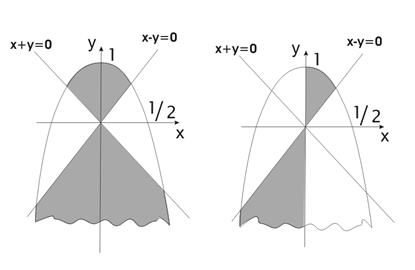
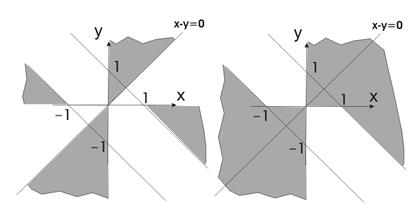
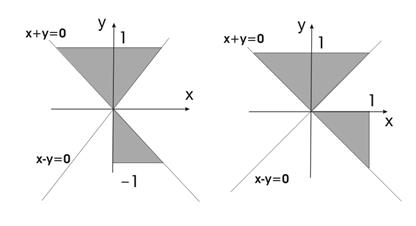
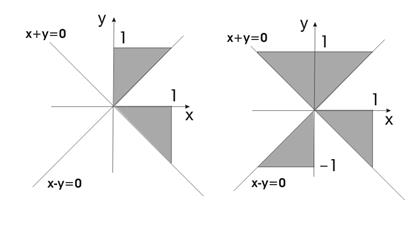
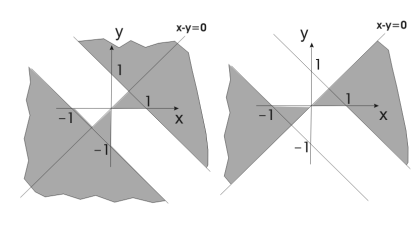
Упражнения Определить принадлежность точки с координатами x,y заштрихованной части плоскости:
1. 2.
3. 4.
5. 6.
7. 8.
9. 10.
11. 12.
13. 14.
15. 16.
17. 18.
19. 20.
21. 22.
23. 24.
25.
Суммирование рядов Пример. Вычисление бесконечной суммы S= Реккурентная формула , связывающая значения последующего слагаемого с предыдущим имеет вид:
Для выхода из цикла суммирования проводится сравнение значения очередного слагаемого и
#include <iostream.h> main() { long double eps,s,y,x; int n; n=0; eps=1.e-5; s=0; y=1.; cin>>x; while(fabs(y)>eps) { s=s+y; n=n+2; y=(-1)*y*x*x/(n*(n-1)); } cout<<s<<" "<<n-2; }
Упражнения Выполнить следующие вычисления: а) задавая x и n (число членов суммы ряда), найти сумму S и
б) задавая x и n (число членов суммы ряда), найти сумму S в порядке убывания индекса до нуля; в) задавая x и
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25.
позиционная запись числа Пример 1. Найти количество цифр в числе и поменять их порядок на обратный. Для решения задачи используем позиционную запись числа в десятичной системе счисления: n=ak-110k-1+ ak-210k-2+ ...+a1101+a0. Остаток от деления n на 10 даст a0. Разделим n на 10 , а результат обозначим через n1 : n1= ak-110k-2+ ak-210k-3+ ...+a2101+a1. Остаток от деления n1 на 10 даст a1. Повторяя операцию деления до тех пор , пока не результат не будет равен 0, найдем все цифры числа n. При этом число шагов деления совпадает с количеством цифр в числе. Образуя сумму по реккурентной формуле mk=mk-110+ ak-1, получим значение числа с обратным порядком цифр.
#include <iostream.h> #include<math.h> main() { int n,m,k; m=0; k=0; cin>>n; while(n>0) { m=10*m+n%10; n=n/10; k=k+1; } cout<<"число цифр :"<<k<<endl; cout<<"палиндром :"<<m<<endl;
Пример 2. Дано натуральное число n . Выбросить из записи числа n цифры 0 и 5,оставив прежним порядок остальных цифр. Процесс нахождения остатков с последующим делением исходного числа на 10 позволяет найти цифры исходного числа в обратном порядке. При образовании суммы числа с удаленными цифрами необходимо цифры исходного числа умножать на 10 в соответствующей степени. Возведение в степень реализуетя с помощью алгоритма умножения на 10 в основном цикле.
#include <iostream.h> #include<math.h> main() { long int n,m,k,l; m=0; k=1; cin>>n; while(n>0) { l=n%10; if(l!=5 && l!=9) { m=m+k*l; k=k*10; } n=n/10; } cout<<m<<endl; }
Пример 3. Найти все трехзначные десятичные числа, сумма цифр которых равна заданному натуральному числу Решение содержит два вложенных цикла по числу единиц и числу десятков. Число сотен вычисляется по заданной сумме цифр.
#include <iostream.h> main() {int n; int i,j,k; do cin>>n; while(n<=0 && n>27); for(i=0;i<=9;i++) for(j=0;j<=9;j++) { k=n-i-j; if(k>=1 && k<=9) cout<<i+j*10+k*100<<endl; }
} Упражнения 1. Определить количество натуральных трехзначных чисел, сумма цифр которых равна заданному числу N. . 2. Среди четырехзначных чисел выбрать те, у которых все четыре цифры различны. 3. Найти количество четных цифр заданного натурального числа N. 4. Найти все симметричные натуральные числа ( палиндромы ) из интервала от К до L. 5. Для данного натурального числа N определить: содержит ли число одинаковые цифры и их количество. 6. Найти все натуральные числа , не превосходящие заданного N, и делящиеся на каждую из своих цифр 7. Найти все натуральные числа , не превосходящие заданного N, десятичная запись которых есть строго возрастающая или строго убывающая последовательность цифр. 8. Найти все пары двухзначных натуральных чисел М и Н таких, что значение произведения М*Н не изменится ,если поменять местами цифры каждого из сомножителей(такой парой будет , например, 38 и 83). 9. Определить сколько раз данная цифра К встречается в целом числе N. 10. Среди двузначных чисел найти те, сумма квадратов цифр которых делится на 13. 11. Даны натуральные числа N. М. Получить все натуральные числа меньшие N. квадрат суммы цифр которых равен М. Написать программу, которая находит все четырехзначные числа КLMN. где К, L, М, N - различные цифры, для которых выполняется соотношение: КL - МN =К+L+М+N 12. Написать программу поиска двузначных чисел, обладающих следующим свойством: если к сумме цифр числа прибавить квадрат этой суммы, то получится снова данное число. 13. Некоторое число оканчивается на 2. Если же эту его последнюю цифру переставить на первое место, то число удвоится. Найти это число. 14. Определить пятизначное число А, удовлетворяющее следующему условию. Образуем два шестизначных числа приписав единицы впереди числа А и в конце его: [1] [А]; [А] [I]. Второе шестизначное число должно быть втрое больше первого:[A][1]/[1][A]=3 15. Квадраты некоторых трехзначных чисел оканчиваются тремя цифрами, которые как раз и составляют исходные числа. Написать программу поиска таких чисел. 16. В трехзначном числе зачеркнули первую цифру слева. Когда полученное двузначное число умножили на 7, то получили исходное число. Найти исходное число. 17. Найти все трехзначные числа, которые при увеличении на 1 делятся на 2, при увеличении на 2 делятся на 3, при увеличении на 3 делятся на 4, а при увеличении на 4 делятся на 5. 18. Найти все трехзначные числа, которые при делении на 2 дают остаток 1, при делении на 3 - остаток 2, при делении на 4 - остаток 3, а само число делится на 5. 19. Найти все двузначные числа, которые при умножении на 2 заканчивается на 8, а при умножении на 3 - на 4. 20. Сумма цифр трехзначного числа кратна 7, само число также делится на 7. Найти все такие числа. 21. Дано четырехзначное число N. Выбросить из записи числа N цифры 0 и 5, оставив прежним порядок остальных цифр. Например, из числа 1509 должно получится 19. . 22. Натуральное число из N цифр является числом Армстронга, если сумма его цифр, возведенных в N-ю степень, равна самому числу ( например, 153 = I3 + 53 + З3). Получить все числа Армстронга, состоящие из трех и четырех цифр. 23. Определить число счастливых билетов в рулоне с номерами билетов от 000000 до 999999. Счастливым считается билет, для которого выполняется условие: N1+N2+N3=N4+N5+N6. 24. Переставить цифры данного натурального числа таким образом, чтобы образовалось наименьшее число, записанное этими цифрами. 25. Если мы сложим все цифры какого-либо числа, затем все цифры найденной суммы и будем повторять этот процесс, мы, наконец, получим однозначное число ( цифру ), называемое цифровым корнем данного числа. Например, цифровой корень числа 34697 равен 2 ( 3+4+6+9+7=29 ; 2+9=11 ; 1+1=2 ). Составить программу для нахождения цифрового корня натурального числа N 26. Найти все автоморфные числа из промежутка от К до L. Автоморфным называется число, квадрат которого заканчивается им самим. Например, автоморфным является число 6, так как его квадрат 36 заканчивается на 6, или число 25 - его квадрат 625. 27. Рассмотрим некоторое натуральное число. Если это не палиндром, то изменим порядок его цифр на обратный и сложим исходное число с получившимся. Если сумма не палиндром, то над ней повторяется, то же действие и т.д., пока не получится палиндром. Даны натуральные числа К, М, Ь ( К < 1.). Проверить, верно, ли, что для любого натурального числа из диапазона от К до Ь процесс завершается не позднее, чем после М таких действий 28. Найти все трехзначные числа, удовлетворяющие следующим условиям: 29. • любые две цифры числа различны ; 30. • число равно среднему арифметическому всех трехзначных чисел (включая данное), состоящих из тех же цифр. 31. Напечатать k- ю цифру последовательности 32. а) 12345678910111213…, в которой выписаны подряд все натуральные числа; 33. б) 110100100010000100000…, в которой выписаны подряд степени 10 ; 34. в)149162536…, …, в которой выписаны подряд квадраты всех натуральных чисел ; г)1123581321…, в которой выписаны подряд все числа Фибоначи Делители целого числа Пример 1. Найти все делители неотрицательного целого числа n. Вариант 1.Самый простой способ решения – это проверить по очереди делимость числа n на каждое из чисел 1,2,3, ... , n. Число операций можно сократить, доказав, что в интервале [n/2+1,n-1] делителей числа n нет. #include <iostream.h> main() { int n,d; cin>>n; for (d=1;d<=n/2;d++) if(n%d==0) cout<<d<<endl; }
Вариант 2. Для нахождения делителей числа n , достаточно обнаружить делители не превышающие значения квадратного корня из числа n. Все остальные делители получаются в результате деления числа n на найденные делители.
#include <iostream.h> main() { int n,d; cin>>n; for (d=1;d*d<n;d++) if(n%d==0) cout<<d<<", "<<n/d<<endl; if(d*d==n) cout<<d<<endl; } Пример 2. Найти наибольший делитель двух неотрицательных целых чисел. Решение основано на алгоритме Евклида, многократно использующим целочисленную операцию деления с остатком: n=q*m+r0, m=q0*r0+r1, r0=q1*r1+r2 .......................... rk-1=qk*rk+rk+1, ........... rj-1=qj*rj, где rj – наибольший общий делитель. #include <iostream.h> main() { long int n,m,r,tmp; cin>>n>>m; if(m>n) { tmp=m; m=n; n=tmp;} while(m>0) { r=n%m; n=m; m=r; } cout<<n; }
Пример 3. Найти все простые числа , меньшие заданного натурального числа n. Вариант 1. Для решения задачи необходимо проверить имеют ли числа из заданного интервала делители, не превышающие значения квадратного корня из числа n.. Четные числа можно не рассматривать, поскольку они делятся на два.
#include <iostream.h> main() { int d,k,n; cin>>n; cout<<1<<endl<<2<<endl<<3<<endl; k=5; while (k<=n) { for (d=2;d*d<=k && k%d!=0;d++) ; if(d*d>k) cout<<k<<endl; k=k+2; } } Упражнения 1. Дано натуральное число N. Получить все его натуральные делители. 2. Найти количество делителей натурального числа N. Сколько из них четных? 3. Найти сумму нечетных делителей натурального числа N. 4. Найти все натуральные числа из интервала от 1 до 200, у которых количество делителей равно N. 5. Найти сумму целых чисел из промежутка от 1 до 200, у которых ровно 5 делителей 6. Найти все целые числа из промежутка от 100 до 300, у которых сумма делителей равна К. 7. Найти натуральное число лежащее в диапазоне от 1 до 10000 с максимальной суммой делителей. 8. Найти все натуральные числа из промежутка от К до L, у которых количество делителей превышает заданное число М. 9. Найти сумму четных делителей натурального числа N. 10. Найти все натуральные числа из промежутка от 1 до 200, у которых сумма четных делителей равна N. 11. Найти количество делителей натурального числа N. больших К. 12. Найти все целые корни уравнения ax3+bx2+cx+d=0 , где a,b,c,d – целые числа. 13. Даны целые числа p и q Получить все делители числа q , взаимно простые с p 14. Дано целое число n .Получить все простые делители этого числа 15. На интервале (1000, 9999) найти все простые числа, каждое из которых обладает тем свойством, что сумма первой и второй цифр в записи этого числа равна сумме третьей и четвертой цифр. 16. Даны натуральные числа К, Ь (К < Ь). Получить все простые числа I, удовлетворяющие неравенству: К < I < Ь, используя решето Эратосфена. 17. Дано натуральное число N > 2. Составить программу разложения этого числа на простые множители. Каждый простой множитель L должен быть выведен k раз, где k-натуральное число, такое, что N делится на Lk и не делится на Lk+1; 18. Дано натуральное число N > 2. Составить программу разложения этого числа на простые множители. Каждый простой множитель должен быть выведен один раз 19. Найти наибольший общий делитель ( НОД ) трех чисел, используя соотношение НОД(К,L,М) = НОД(НОД( К, L ), M) и алгоритм Евклида 20. Даны натуральные числа М, N. Получить все кратные им числа, меньшие МхN 21. Для натуральных чисел К и L определить наименьшее общее кратное (НОК), используя соотношение: НОД (K,L)=KL/ НОД (K,L) Даны M ( М > 2 ) натуральных чисел: N1,N2, ..., Nм. Вычислить НОД (N1,N2, ..., Nм ), используя соотношение НОД(N1,N2, ..., Nм)= НОД(НОД(N1,N2, ..., Nм-1 ), Nм ) и алгоритм Евклида. . 22. Найти все простые несократимые дроби, заключенные между 0 и 1, знаменатели которых не превышают 7 (дробь задается двумя натуральными числами - числителем и знаменателем ) 23. . Составить программу сложения двух дробей. Результат сложения - несократимая дробь 24. Составить программу для нахождения всех совершенных чисел, меньших заданного числа N. Совершенным называется число, равное сумме всех своих положительных делителей ( включая единицу, но исключая само число ). Например, 28 - совершенное число, т.к. 28 = 1 + 2 + 4 + 7 + 14.. 25. Даны натуральные числа N. М. Найти все пары натуральных дружественных чисел, лежащих в диапазоне от N до М. Два числа называются дружественными, если каждое из них равно сумме всех делителей другого ( само число в качестве делителя не рассматривается). .
Поиск по сайту: |
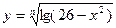 . Значение переменной x и параметра n вводить с клавиатуры (n – целое).
. Значение переменной x и параметра n вводить с клавиатуры (n – целое). при x=3,5; a=0.2; -1,5 b=2; 3
при x=3,5; a=0.2; -1,5 b=2; 3 ; при x=0.3; a=2,1; 9,8 b=1; 6;
; при x=0.3; a=2,1; 9,8 b=1; 6;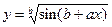 ; при x=1.03; a=2,5; 0,3; b=2; 3
; при x=1.03; a=2,5; 0,3; b=2; 3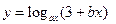 ; при x=0.3; a=0,2; -1,2 b=6; -1
; при x=0.3; a=0,2; -1,2 b=6; -1 ; при x=1.3; a=0,2; 3,1; b=2; 3;
; при x=1.3; a=0,2; 3,1; b=2; 3;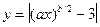 ; при x=2.3; a=1,2; -1,5; b=2; 3;
; при x=2.3; a=1,2; -1,5; b=2; 3;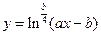 ; при x=1.03; a=1,2; 4,5; b=4; 1;
; при x=1.03; a=1,2; 4,5; b=4; 1; ; при x=1.03; a=-4; -5.2; b=6; 1
; при x=1.03; a=-4; -5.2; b=6; 1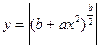 ; при x=2.3; a=-1.2; 0,3 b=2; 3
; при x=2.3; a=-1.2; 0,3 b=2; 3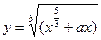 ; при x=-1.3; a=-2,2; 1,1 b=2; 3 11.
; при x=-1.3; a=-2,2; 1,1 b=2; 3 11.  ; при x=1.03; a=-1,2; 2,3 b=3; 2
; при x=1.03; a=-1,2; 2,3 b=3; 2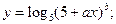 при x=3,5; a=0.2; -1,5 b=2; 3
при x=3,5; a=0.2; -1,5 b=2; 3 ; при x=0.3; a=2,1; 9,8 b=1; 6;
; при x=0.3; a=2,1; 9,8 b=1; 6;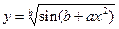 ; при x=1.03; a=2,5; 0,3; b=2; 3
; при x=1.03; a=2,5; 0,3; b=2; 3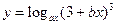 ; при x=0.3; a=0,2; -1,2 b=6; -1
; при x=0.3; a=0,2; -1,2 b=6; -1 ; при x=1.3; a=0,2; 3,1; b=2; 3;
; при x=1.3; a=0,2; 3,1; b=2; 3;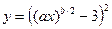 ; при x=2.3; a=1,2; -1,5; b=2; 3;
; при x=2.3; a=1,2; -1,5; b=2; 3;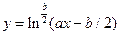 ;при x=1.03; a=1,2; 4,5; b=2; 3;
;при x=1.03; a=1,2; 4,5; b=2; 3; ; при x=1.03; a=-4; -5.2; b=6; 1
; при x=1.03; a=-4; -5.2; b=6; 1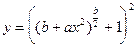 ; при x=2.3; a=-1.2; 0,3 b=2; 3
; при x=2.3; a=-1.2; 0,3 b=2; 3 ; при x=-1.3; a=-2,2; 1,1 b=2; 3
; при x=-1.3; a=-2,2; 1,1 b=2; 3 ; при x=1.03; a=-1,2; 2,3 b=3; 2
; при x=1.03; a=-1,2; 2,3 b=3; 2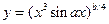 ; при x=1.3; a=0,2; 3,1; b=4; 5;
; при x=1.3; a=0,2; 3,1; b=4; 5; ; при x=2.3; a=1,2 ;-1,5; b=4; 5;
; при x=2.3; a=1,2 ;-1,5; b=4; 5; ; при x=1.03; a=1,2; 4,5; b=2; 3;
; при x=1.03; a=1,2; 4,5; b=2; 3;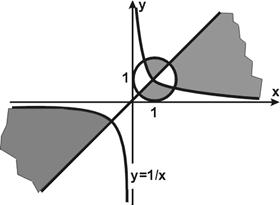






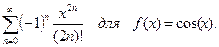 с заданной точностью
с заданной точностью 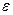 . Считается , что заданная точность достигается ,если вычислена сумма нескольких первых слагаемых и очередное слагаемое оказалось по модулю меньше, чем
. Считается , что заданная точность достигается ,если вычислена сумма нескольких первых слагаемых и очередное слагаемое оказалось по модулю меньше, чем 
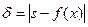 ;
;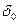 , найти сумму S и число членов суммы n. Суммирование выполнять до тех пор, пока не выполнится условие:
, найти сумму S и число членов суммы n. Суммирование выполнять до тех пор, пока не выполнится условие: