 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вычисление кратных интегралов методом Монте-Карло ⇐ ПредыдущаяСтр 4 из 4
Пусть функция
Геометрически число I представляет собой (m+1)-мерный объём прямого цилиндроида в пространстве Преобразуем интеграл (1) так, чтобы новая область интегрирования целиком содержалась внутри единичного m-мерного куба. Пусть область S расположена в m-мерном параллелепипеде
Сделаем замену переменных Тогда, очевидно, m-мерный параллелепипед (2) преобразуется в m-мерный единичный куб и, следовательно, новая область интегрирования σ, которая находится по обычным правилам, будет целиком расположена внутри этого куба. Вычисляя якобиан преобразования, будем иметь:
где Укажем способ вычисления интеграла (5/) методом случайных испытаний. Выбираем m равномерно распределённых на отрезке [0, 1] последовательностей случайных чисел:
Точки 1. 2. (для удобства мы здесь изменяем нумерацию точек). Заметим, что относительно границы Г области σ следует заранее договориться, причисляются ли граничные точки или часть их к области σ, или не причисляются к ней. В общем случае при гладкой границе Г это не имеет существенного значения; в отдельных случаях нужно решать вопрос с учётом конкретной обстановки. Взяв достаточно большое число n точек Заключение. Метод Монте-Карло используется очень часто, порой некритично и неэффективным образом. Он имеет некоторые очевидные преимущества: а) Он не требует никаких предложений о регулярности, за исключением квадратичной интегрируемости . Это может быть полезным, так как часто очень сложная функция, чьи свойства регулярности трудно установить. б) Он приводит к выполнимой процедуре даже в многомерном случае, когда численное интегрирование неприменимо, например, при числе измерений, большим 10. в) Его легко применять при малых ограничениях или без предварительного анализа задачи. Он обладает, однако, некоторыми недостатками, а именно: а) Границы ошибки не определены точно, но включают некую случайность. Это, однако, более психологическая, чем реальная, трудность. б) Статическая погрешность убывает медленно. в) Необходимость иметь случайные числа. Приложение. Равномерно распределённые случайные числа 10 09 73 25 33 76 52 01 35 86 34 67 35 48 76 80 95 90 9117 37 54 20 48 05 64 89 47 42 96 24 80 52 40 37 20 63 61 04 02 08 42 26 89 53 19 64 50 93 03 23 20 90 25 60 15 95 33 47 64 99 01 90 25 29 09 37 67 07 15 38 31 13 11 65 88 67 67 43 97 12 80 79 99 70 80 15 73 61 47 64 03 23 66 53 98 95 11 68 77 66 06 57 47 17 34 07 27 68 50 36 69 73 61 70 65 81 33 98 85 31 06 01 08 05 45 57 18 24 06 35 30 34 26 14 86 79 90 74 39 85 26 97 76 02 02 05 16 56 92 68 66 57 48 18 73 05 38 52 47 63 57 33 21 35 05 32 54 70 48 90 55 35 75 48 28 46 82 87 09 73 79 64 57 53 03 52 96 47 78 35 80 83 42 82 60 93 52 03 44 Список литературы Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов втузов. – 3-е изд., перераб. И доп. – М.: Высш. школа, 1979г. Ермаков С. М. Методы Монте-Карло и смежные вопросы. М.: Наука, 1971г. Севастьянов Б. А. Курс теории вероятностей и математической статистики. – М.:Наука,1982г. Математика. Большой энциклопедический словарь / Гл. ред. Ю. В. Прохоров. – М.: Большая Российская энциклопедия,1999г. Гмурман В. Е. Теория вероятностей и математическая статистика. Учеб. пособие для втузов. Изд. 5-е, перераб. и доп. М., «Высш. школа», 1977.
Поиск по сайту: |
 непрерывна в ограниченной замкнутой области S и требуется вычислить m-кратный интеграл
непрерывна в ограниченной замкнутой области S и требуется вычислить m-кратный интеграл
 . (1)
. (1) , построенного на основании S и ограниченного сверху данной поверхностью
, построенного на основании S и ограниченного сверху данной поверхностью 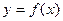 , где
, где  .
. . (2)
. (2)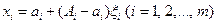 . (3)
. (3)
 (4)
(4) . Таким образом,
. Таким образом, 
 , (5)
, (5) . Введя обозначения
. Введя обозначения  и
и  , запишем интеграл (5) короче в следующем виде:
, запишем интеграл (5) короче в следующем виде:  . (5/)
. (5/)
 можно рассматривать как случайные. Выбрав достаточно большое N число точек
можно рассматривать как случайные. Выбрав достаточно большое N число точек  , проверяем, какие из них принадлежат области σ (первая категория) и какие не принадлежат ей (вторая категория). Пусть
, проверяем, какие из них принадлежат области σ (первая категория) и какие не принадлежат ей (вторая категория). Пусть при i=1, 2, …, n (6)
при i=1, 2, …, n (6)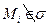 при i=n+1, n+2, …,N (6/)
при i=n+1, n+2, …,N (6/) , приближённо можно положить:
, приближённо можно положить:  ; отсюда искомый интеграл выражается формулой
; отсюда искомый интеграл выражается формулой  , где под σ понимается m-мерный объём области интегрирования σ. Если вычисление объёма σ затруднительно, то можно принять:
, где под σ понимается m-мерный объём области интегрирования σ. Если вычисление объёма σ затруднительно, то можно принять:  , отсюда
, отсюда 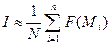 . В частном случае, когда σ есть единичный куб, проверка становится излишней, то есть n=N и мы имеем просто
. В частном случае, когда σ есть единичный куб, проверка становится излишней, то есть n=N и мы имеем просто  .
.