 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Самокорректирующиеся коды
Коды, в которых возможно автоматическое исправление ошибок, называются самокорректирующимися. Для построения самокорректирующегося кода, рассчитанного на исправление одиночных ошибок, одного контрольного разряда недостаточно. Как видно из дальнейшего, количество контрольных разрядов k должно быть выбрано так, чтобы удовлетворялось неравенство
В настоящее время наибольший интерес представляют двоичные блочные корректирующие коды. При использовании таких кодов информация передаётся в виде блоков одинаковой длины и каждый блок кодируется и декодируется независимо друг от друга. Почти во всех блочных кодах символы можно разделить на информационные и проверочные. Таким образом, все комбинации кодов разделяются на разрешенные (для которых соотношение информационных и проверочных символов возможно) и запрещенные. Основными характеристиками самокорректирующихся кодов являются: 1. Число разрешенных и запрещенных комбинаций. Если n - число символов в блоке, r - число проверочных символов в блоке, k - число информационных символов, то 2. Избыточность кода. Величину 3. Минимальное кодовое расстояние. Минимальным кодовым расстоянием d называется минимальное число искаженных символов, необходимое для перехода одной разрешенной комбинации в другую. 4. Число обнаруживаемых и исправляемых ошибок. Если g - количество ошибок, которое код способен исправить, то необходимо и достаточно, чтобы 5. Корректирующие возможности кодов.
Аксиомы и модели булевой алгебры. Понятие изоморфизма. Основные понятия алгебры логики. Булевой алгеброй называется непустое множество A с двумя бинарными операциями Основными понятиями булевой алгебры являются понятия логической переменной и логической функции. Логической переменной называется величина, которая может принимать одно из двух возможных состояний (значений), одно из которых обозначается символом “0”, другое – “1” Логической (булевой) функцией (обычное обозначение – у) называется функция двоичных переменных (аргументов), которая также может принимать одно из двух возможных состояний (значений): “0” или “1”.
Модель формальной логики в рамках булевой алгебры · «Переменные» — булевы переменные из множества {0,1}. · Знаки Подстановкой всех возможных A, B, C в аксиомы убеждаемся, что в этой модели выполняются все аксиомы. Точно так же проверяется истинность modus ponens. Модель планиметрии в рамках арифметики «Точка» — пара действительных чисел «Прямая» — все точки, для которых «Плоскость» — все возможные пары действительных чисел Изоморфи́зм (от др.-греч. ἴσος — «равный, одинаковый, подобный» и μορφή — «форма») — это очень общее понятие, которое употребляется в различных разделах математики. В общих чертах его можно описать так: пусть даны два множества с определённой структурой (группы, кольца, линейные пространства и т. п.). Биекция между ними называется изоморфизмом, если она сохраняет эту структуру. Если между такими множествами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаётотношение эквивалентности на классе таких множеств со структурой. Объекты, между которыми существует изоморфизм, являются в определённом смысле «одинаково устроенными», они называются изоморфными. Классическим примером изоморфных систем могут служить множество
Поиск по сайту: |
 или
или 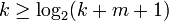 , где m — количество основных двоичных разрядов кодового слова. Минимальные значения k при заданных значениях m, найденные в соответствии с этим неравенством, приведены в таблице.
, где m — количество основных двоичных разрядов кодового слова. Минимальные значения k при заданных значениях m, найденные в соответствии с этим неравенством, приведены в таблице. - число возможных кодовых комбинаций,
- число возможных кодовых комбинаций,  - число разрешенных кодовых комбинаций,
- число разрешенных кодовых комбинаций,  - число запрещенных комбинаций.
- число запрещенных комбинаций. называют избыточностью корректирующего кода.
называют избыточностью корректирующего кода.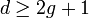
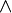 (аналог конъюнкции),
(аналог конъюнкции),  (аналог дизъюнкции), унарной операцией
(аналог дизъюнкции), унарной операцией  (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:
(аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для всех a, b и c из множества A верны следующие аксиомы:



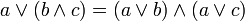


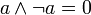



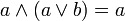
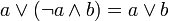





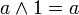



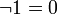


 и
и 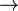 — соответствующие операции булевой алгебры.
— соответствующие операции булевой алгебры.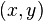 .
. , где
, где 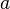 и
и 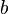 одновременно не равны 0.
одновременно не равны 0. всех вещественных чисел с определённой на нём операцией сложения и множество
всех вещественных чисел с определённой на нём операцией сложения и множество  положительных вещественных чисел с заданной на нём операцией умножения. Отображение
положительных вещественных чисел с заданной на нём операцией умножения. Отображение  в этом случае является изоморфизмом.
в этом случае является изоморфизмом.